Пусть Са*ь есть число сетей, соединенных с а и Ь и не соединенных с другими элементами В но соединенных по крайней мере с одним элементом Bj. Аналогично Ссь* - число сетей, связанных с а и 6 и не соединенных с другими элементами Вг, но соединенных по крайней мере с одним (другим) элементом Bi. Тогда формулировку леммы 7.2 можно изменить следующим образом.

Лемма 7.4. В результате перемены местами элементов а е Bj и 6 е Вг число соединений уменьшается на D* -f D* - 2Са*ь* -

- Са*Ь - СаЬ*.

Доказательство. Предлагается провести самостоятельно.

Заметим, что Са*ь и Саъ* не являются постоянными величинами, а зависят от разбиения. Следовательно, определение наилучшей пары меняемых местами элементов и пересчет ранее определенных значений D* существенно усложняются.

Для разбиения множества из 5 элементов на два, содержащих 1 и 2 элементов соответственно (где щ и не обязательно равны между собой), мы должны задаться исходным разбиением на два множества, одно из которых содержит п\, а другое 2 элементов, и затем произвести оптимальным образом min(ni, Пг) замен элементов. В случае если необходимо произвести разбиение множества 5 на два множества, имеющих не менее ь но не более пг п\ элементов каждое (где п\ + п), мы можем добавить к S еще 2п2 - п фиктивных элементов. При этом будем считать, что эти элементы не соединены с другими. Затем разбиваем множество на два равномощных подмножества, производим пг обменов одиночными элементами, оптимизируя, таким образом, разбиение, после чего удаляем фиктивные элементы.

Представляется возможным повторное применение этой процедуры для разбиения множества на k непересекающихся подмножеств путем разбиения его на два блока и последующего применения к этим блокам указанной процедуры. С другой стороны, мы можем образовать исходное разбиение из k множеств

и применить к ним алгоритм разбиения ко всем парам

подмножеств.

Вообще говоря, проведение оптимизации для некоторой пары Bj и Bj изменяет Bj, поэтому может потребоваться повторное рассмотрение пар подмножеств В^ и В^. Для схем с сетями, имеющими много выходных зажимов, указанная процедура может усложниться, так как некоторые сети могут соединять элементы более чем двух различных подмножеств. Следовательно, оптимизация, проведенная для подмножеств Вг и В может увеличить общее число соединений как между Bj, и В^, так и между Bj и Bfe. Поэтому при проведении оптимизации данной

7.4.2. КОНСТРУКТИВНЫЕ ЭВРИСТИЧЕСКИЕ ПРОЦЕДУРЫ РАЗБИЕНИЯ

Итеративная процедура Кернихана - Лина основана на пошаговом улучшении исходного разбиения. Заметим, что конструктивные процедуры не требуют такого исходного разбиения. В большинстве конструктивных процедур разбиения предпринимается попытка сгруппировать сильно связанные элементы (т.е. элементы, имеющие много соединений друг с другом) в пучки [5] или группы. В некоторых такого рода алгоритмах размер пучка не ограничивается. В силу того что естественно образованные группы могут быть слишком велики по сравнению с требуемыми размерами модуля, может возникнуть необходимость в дальнейшем разбиении пучков на части соответствующего размера. Ниже описана процедура [30], которую полезно применять для разбиения схем в том случае, когда на число выводов карты наложены более строгие ограничения, чем на число элементов одной карты.

пары подмножеств может возникнуть необходимость рассмотрения соединений с другими подмножествами.

Одно из ограничений применения этого алгоритма состоит в том, что алгоритм оперирует скорее с ограничениями на максимальное число элементов в одном модуле, чем на максимальное число соединений одного модуля с другими. Таким образом, эффективное применение этого алгоритма при рассмотрении ограничений одновременно и на число элементов и на число внешних соединений модулей может оказаться затруднительным. Указанный алгоритм работает путем улучшения допустимых решений. Поэтому его целесообразно использовать вместе с процедурами другого типа, ориентированными на получение исходных разбиений.

Различают итеративные и конструктивные процедуры. Итеративные процедуры, как, например, процедура 7.1, последовательно модифицируют существующее решение с целью его улучшения. На основе рассмотрения отдельных элементов конструктивные алгоритмы позволяют строить решения для отдельных подзадач, которые затем объединяют для получения полного решения.

На основе целесообразного выбора начального разбиения представляется возможным увеличить вероятность нахождения оптимального решения с помощью итеративной процедуры. Далее мы рассмотрим некоторые конструктивные алгоритмы построения исходного разбиения, которые могут быть использованы совместно с процедурой 7.1.

Пусть задана некоторая схема. Сети, соединенные с выводами этой схемы, назовем инициирующими. Каждая сеть, соединенная с элементом, является для него либо входной, либо выходной (т. е. представляющий схему биграф является ориентированным). Так как с выводами схемы соединяются только инициирующие сети, их можно использовать для построения пучков.

Процедура 7.2

1. Выбираем множество N инициирующих сетей.

2. Для каждой инициирующей сети Ni е N, не являющейся входом схемы, определяем пучок G, следующим образом. Любой элемент е для которого Ni является выходной сетью, принадлежит Gj. Допустим, что N является входной сетью некоторого элемента из Gj. Тогда, если N не является инициирующей сетью, включаем в G, элементы, для которых N будет выходной сетью. Построение пучка G, завершается тогда, когда к нему нельзя добавить ни одного нового элемента. (Этот шаг соответствует продвижению от одной инициирующей сети вплоть до другой инициирующей сети.)

Процедура образования пучков для заданного множества инициирующих сетей определена алгоритмически. Однако выбор инициирующих сетей производится на основе эвристической процедуры. Для выбора инициирующих сетей могут быть предложены следующие правила:

1. Входы и выходы комбинационных схем должны выбираться из множества инициирующих сетей.

2. Входы и выходы последовательностных схем должны выбираться в качестве инициирующих сетей. Для комбинационных схем входы и выходы надо выбирать из множества инициирующих сетей. Для последовательностных схем в качестве инициирующих сетей надо выбирать входы и выходы схемы. Кроме того, надо выбрать в качестве инициирующих сетей выходы элементов памяти. Если в контуре обратной связи не содержится элементов памяти, то они также могут быть выбраны в качестве инициирующих.

3. Для уменьшения размера пучков или для того, чтобы получить непересекающиеся пучки, надо добавить дополнительные инициирующие сети.

В зависимости от выбора инициирующих сетей на основе процедуры 7.2 могут быть получены и пересекающиеся пучки; это приводит к схемным реализациям с использованием дублирования элементов. Непересекающиеся пучки могут быть получены путем специального выбора инициирующих сетей, причем е зависимости от выбора инициирующих сетей эти пучки могут

как удовлетворять, так и не удовлетворять ограничениям на число элементов в одном модуле. Если в одной группе окажется слишком много элементов, то ее нужно разделить на подгруппы. По-видимому, эту процедуру целесообразнее использовать при условии, когда ограничения на число выводов модулей оказываются более строгими, чем ограничение размеров самих модулей.

Пример 7.3. Для схемы, изображенной на рис. 7.П, инициирующими сетями являются N\, N2, N3, N4, Л/5, Л^б, определяе-

£6

1з £

т

Рис. 7.11 Схема из примера 7.3.

мые входами /ь /г, h и выходами Оь О2, Ог. Сеть N4 опреде* ляет пучок {Е\,Е2,ЕЗ,ЕЪ,ЕЩ. Сеть Л/5 определяет пучок {£1, Е2,ЕЗ,Е4,Е&}. Сеть определяет пучок {£7, £8, £10, £11}. Если в качестве инициирующих выбрать также сети N7 и Л/8, то полученные пучки {£1,£2}, {£3}, {£4, £6}, {£5, £9}, {£7, £8, £10, £11} будут непересекающимися.

Рассмотрим теперь конструктивную процедуру образования пучков, каждый из которых содержит не более заданного граничного числа элементов. Такие пучки назовем допустимыми пучками. Для схемы, содержащей только двухэлементные сети (т. е. соединения с двумя зажимами)., обозначим через Сц число соединений между элементами е, и Cj. Множество 5, содержащее т элементов, называется т-пучком с весом к, где k =

= Zl Cij. Алгоритм построения пучков подразумевает на-i, /s s

хождение допустимых пучков с большими весами. Использование пучков с большими весами позволяет уменьшить число соединений между пучками. Такой подход можно применить для последовательного или параллельного построения модулей разбиения, как это имеет место в следующих процедурах.

Процедура 7.3 (последовательное разбиение)

1. Пусть 5 - предназначенное для разбиения множество элементов. Выбираем элемент е, из 5, который имеет наибольшее общее число соединений с другими элементами, и используем этот элемент для образования пучка Ci. Удаляем элемент е-, из 5.

2. Включаем в Q элемент eeS, который максимизирует Yj Ckj. В ТОМ случае, когда таких элементов несколько, вы-

бираем элемент с минимальным общим числом соединений. (Это позволяет уменьшить число соединений между модулями.) Удаляем е,- из 5.

3. Повторяем шаг 2 до тех пор, пока Q содержит т элементов.

4. Применяем шаги 1-3 к остающимся элементам до тех пор, пока все элементы не будут размещены по допустимым пучкам.

Другая эвристическая процедура позволяет осуществить параллельное образование нескольких пучков. В этой процедуре множество из п элементов разбивается на модули, содержащие не более т элементов каждый. При этом сначала выбирается множество из [п/т] элементов (называемых зернами), вокруг которых формируются пучки. Далее эта процедура будет описана подробнее.

Процедура 7.4 (параллельное разбиение)

1. Выбираем элемент ег е5, имеющий наибольНиее число соединений с другими элементами. Если таких элементов несколько, то выбираем любой из них. Элемент ei будет зерном для пучка Gi. Удаляем из 5.

2. Выбираем в качестве зерна элемент е имеющий наименьшее число соединений с ранее выбранными зернами. Если таких элементов несколько, то выбираем элемент, имеющий наибольшее число соединений с элементами из 5, не являющимися зернами. Удаляем из 5.

3. Повторяем шаг 2 до тех пор, пока не будут выбраны [n/m] зерен.

4. Для каждого элемента е 5 и для каждого пучка Gi, содержащего менее т элементов, вычисляем число С {ей, Gi) соединений между и элементами из Gi. Находим элемент

и пучок Gj, для которых С (ей, Gj) максимально. Включаем ей в пучок Gj и удаляем из 5. При наличии выбора выбираем элемент с наименьшим числом соединений.

5. Повторяем шаг 4 до тех пор, пока все элементы не будут распределены по пучкам.

Если на максимальное число соединений одного пучка наложены ограничения, то процедуры как последовательного, так и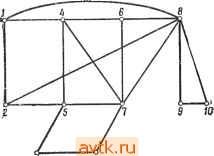

3 If

Рис. 7.12. Граф из примера 7.4.

И распределением их. по исходным пучкам. При некоторых промежуточных значениях k и k такая обобщенная процедура может обеспечить лучшие решения.

Во всех описанных процедурах существует возможность возникновения на некотором шаге нескольких равноправных вариантов выбора. Мы предположим, что такие ситуации разрешаются произвольным образом или на основе некоторого эвристического правила. На основе дополнительных вычислительных затрат можно также ввести просмотр вперед , т. е. оценку последствий выбора различных вариантов.

Пример 7.4. Пусть требуется разбить вершины изображенного на рис. 7.12 графа на два модуля с шестью или менее вершинами каждый. Пользуясь процедурами последовательного разбиения, выбираем для образования пучка вершину 8, имеющую максимальное число соединений. Вершины 1, 2, 7, 9 и 10 имеют единственное соединение с вершиной 8, но среди них минимальное число соединений с другими вершинами имеют вершины 9 и 10. Выбираем произвольно вершину 9, а затем включаем в пучок вершину 10, так как у нее есть два соединения

параллельного разбиения должны быть модифицированы. Как показывает опыт, все образованные при помощи процедуры последовательного разбиения пучки, кроме тех, которые сформированы из остатков , являются сильносвязными. В процедуре параллельного разбиения отбор удачных зерен оказывается сложным, поскольку они отбираются еще до начала формирования пучков. Описанные процедуры можно'представить как специальные экстремальные случаи некоторой общей процедуры, обеспечивающей образование исходных пучков, содержащих по k элементов, с последующим формированием (из еще нераспределенных элементов) пучков, содержащих по k элементов.

С пучком. Продолжая процедуру, прибавляем вершины 1 (или

2, или 6), 2 и 6 и получаем пучок {1,2,6,8,9,10}. Оставшиеся вершины {3,4,5,7,11} образуют другой модуль. Число соединений между модулями оказывается равным 5.

Используя процедуру параллельного разбиения, мы выбираем вершину 8 в качестве зерна первого пучка Gi. Вершины

3, 4, 5 и 11 могут быть выбраны в качестве зерен, так как все они имеют минимальное число (0) соединений с вершиной 8. Среди них элементы 4 и 5 имеют максимальное количество (4) соединений с другими вершинами. Пусть в качестве зерна второго пучка Сг выбрана (произвольно) вершина 4. Вычисляем величины С(еи,Сг) для всех вершин. Для некоторых вершин

Oi

Рис. 7.13. Схема, содержащая многооконечную сеть.

С(е^, Gi) = 1, но среди них С(9, Gi) = С(10, d) = 1, и вершины 9 и 10 имеют наименьшее число (2) соединений. Произвольно включаем в пучок Gi вершину 9. На следующем шаге С(10, Gl) = 2, и в Gl включается также вершина 10.

На этом этапе у нас есть возможность выбора, а именно включить вершины 1, 2 или 6 или в пучок Gi, или в Gg. Поскольку в пучке Сг меньше вершин, включаем одну из этих вершин в Сг. Просмотр вперед для выбора одной из вершин 1, 2 и 6 показывает, что лучшим является выбор вершины 6, так как получающийся пучок {4,6} имеет только два соединения с вершиной 7, в то время как пучки {1,4} и {2,4} не имеют по два соединения ни с одной вершиной. На этом этапе Gi = = {8,9, 10} и G2 = {4,6}. Затем мы включаем вершины 7 и вершину 5 в пучок G2, после чего включаем в него же вершины 3 и 11. Оставшиеся элементы должны быть включены в пучок Gi, таким образом, образуются пучки С, = {1, 2,8,9, 10} и Ga = = (3,4,5,6,7,11}, имеющие между собой четыре соединения.

В случае схем с сетями с большим числом внешних зажимов (многооконечными сетями) процедуры 7.3 и 7.4 необходимо несколько модифицировать. Если связанные одной сетью эле-

Е2, Е4, £6} £ 1, Е2, ЕЗ, £4, £5} £1, £2} £3, £6}

Nj {£4, £5, £6}

Сети Nl, N2 Ns и Л^д определяют пучки, состоящие только из одного элемента.

Если все элементы определяемого сетью пучка находятся в одном модуле, то для реализации этой сети не потребуется специального соединения между модулями. Таким образом, целесообразно начинать процедуру разбиения с определяемого некоторой сетью пучка, удовлетворяющего ограничениям на число элементов в модуле. Большие пучки образуются путем включения в исходный пучок других пучков, определяемых другими сетями при условии соблюдения ограничений на размер модуля.

Пусть требуется разбить схему, изображенную на рис. 7.13, на два модуля, каждый из которых содержит не более четырех элементов. Используя процедуру последовательного разбиения, выбираем в качестве исходного пучок {Е2, ЕА, £6}, определяемый сетью Л^з. Легко заметить, что пучок, определяемый Nz, Nq или Nj, можно добавить к исходному при соблюдении ограничений на число элементов модуля. В том случае, если выбирается пучок, определяемый N5, результирующим разбиением будет {£1, £2, £4, £6, £3, £5}, что соответствует рис. 7.14, а. При таком разбиении элементы пучков, определяемых сетями Л/4, Ne и N7, находятся в разных модулях. При этом потребуются три соединения между модулями, а число выводов будет равно И, как показано на рис. 7.14, а. Другими возможными решениями при том же исходном пучке являются {£2, £3, £4, £6; £1, £5}, требующие три соединения между модулями, и {£2, £4, £5, £6; £1,£3}, требующие только два соединения.

В процедуре параллельного разбиения отыскиваются два исходных непересекающихся пучка, дополняемых пучками, опре-

менты включаются в два различных модуля, то для объединения всех этих элементов достаточно единственного соединения между двумя модулями независимо от числа соединяемых элементов. Для уменьшения общего числа выводов всех модулей можно использовать и тот факт, что каждое соединение между модулями требует лишь двух выводов, в то время как внешняя линия, соединенная с сетью, требует только один вывод.

В случае многооконечных сетей с большим числом внешних выводов целесообразно рассматривать пучки, определяемые сетями. В следующей таблице приведены определяемые сетями пучки для схемы, изображенной на рис. 7.13:

Определяющая сеть Пучок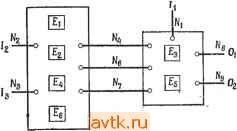

Рис. 7.14. Два варианта разбиения схемы рис. 7.13.

Объединяя оба эвристических подхода, последовательный и параллельный, можно привести следующую весьма общую формулировку общей процедуры:

1. Правило выбора элемента - выбор элемента для последующего рассмотрения.

2. Правило построения разбиения - для полученного с помощью правила выбора элемента определяется его место в окончательном разбиении на основе определения локально-оптимального решения в соответствии с некоторой эвристической функцией цели.

3. Повторение операций, предусмотренных пп. 1 и 2, до тех пор, пока не будет получено окончательное решение.

Из дальнейшего будет понятно, что аналогичным образом можно сформулировать конструктивные эвристики и для реше-

деляемьши другими сетями. Таким образом, для изображенной на рис. 7.13 схемы, начиная с {El, Е2} и {£3, £6} или {£4, £5, £6}, мы получаем разбиение {£1, £2; £3, £4, £5, £6}. При таком разбиении требуются два соединения между модулями и восемь выводов. Разбиение с восемью выводами и только одним соединением между модулями получается путем соединения входа /з с обоими модулями.

ния других задач, в частности для решения задач разбиения и размещения было предложено множество конкретных вариантов этбй общей процедуры.

7.5. РАЗБИЕНИЕ, МИНИМИЗИРУЮЩЕЕ ДЛИТЕЛЬНОСТЬ ЗАДЕРЖКИ

Общая длительность задержки, связанная с внутримодуль-ными соединениями схемы, значительно меньше, чем длительность задержки, связанная с соединениями между модулями. Поэтому другим критерием оптимизации разбиения схемы является минимизация максимальной длительности задержки [21].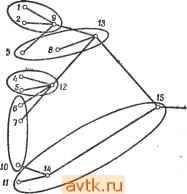

Рис. 7.15. Разбиение графа, обеспечивающее длительность задержки, равную 3.

При этом предполагается, что внутримодульные соединения имеют нулевую, а межмодульные соединения единичную задержку. Каждый модуль содержит максимум М логических элементов и Р выводов. Так, например, при разбиении изображенного на рис. 7.15 графа, каждая вершина которого представляет один логический элемент, задержка определяется максимальным (по всем путям от входа к выходу) числом соединений между модулями. В данном случае задержка равна трем, такую задержку создают многие сигнальные пути, одним из которых является путь, определяемый последовательностью вершин 3 - - 9-13-15.

В том случае, когда в схеме есть петля обратной связи между модулями, задержка в схеме зависит от скорости наступления стабилизации. Чтобы не рассматривать здесь процесс стабилизации, ограничимся рассмотрением ациклических графов. Схему с обратной связью можно представить р виде такого