мых множеств, - это содержащие элемент множества [е\, ег, бз} и [ви 64, 65}. Разбиение (в котором каждый элемент входит только в одно множество) с минимальным числом соединений можно получить, если произвольным образом исключить все повторные вхождения каждого элемента. Для множеств {бь ег, ез} и {е е4, eg} получаем {е eg, 63} и {е4, е^} или {ег, ез} и {е е^, еь).

Очевидно, что между этой процедурой и процедурой покрытия простыми импликантами существует определенное соответствие и практическое их применение целесообразно и возможно только для задач относительно малой размерности. Рассмотрим два множества элементов Ti, Гг, таких, что Ti s Гг, тогда если Tl не является допустимым, то и Гг не является допустимым. Следовательно, допустимые множества могут формироваться путем объединения меньших множеств подобно тому, как это делается в процедуре Куина- Мак-Класки. Однако это не так в том случае, когда мы рассматриваем ограничения не на число электрических соединений карты, а на число внешних электрических соединений, т. е. сигналов, которые выводятся с карты. (Это ограничение более существенно в силу того, что внутренние соединения не требуют выводов.) Например, в схеме, граф которой изображен на рис. 7.3, множество {е е4} имеет пять сетей, Ni, n2, N3, N4 и Ne, каждая из которых является входом или промежуточным соединением и, следовательно, не является допустимым в случае, когда число выводов карты меньше четырех. Множество элементов {ej, ег, е4}, напротив, требует только четырех выводов для сигналов n2, N3, i, Ne, {n1 является внутренним соединением для этого множества элементов) и является, следовательно, допустимым. Таким образом, получение допустимых множеств (при такой интерпретации ограничений на электрические соединения) усложняется. Следовательно, подобное решение задачи о разбиении представляет ограниченный практический интерес.

7.3.2. СВЕДЕНИЕ К ЗАДАЧЕ

МАТЕМАТИЧЕСКОГО ПРОГРАММИРОВАНИЯ

Оптимальные решения задачи о разбиении могут быть получены при помощи громоздких процедур полного перебора или таких их усовершенствований, как метод ветвей и границ. Число различных разбиений п компонент на k блоков одного размера р равняется п\/{к\{р\)). Если размеры блоков различны, то это число еще больше. Поскольку число разбиений с ростом п резко возрастает, процедуры, связанные с полным или усовершенствованным перебором, применимы лишь для небольших схем.

Задача разбиения графов (для схем с двухоконечными сетями) может быть сформулирована как задача целочисленного

программирования с переменными, принимающими значения либо О, либо 1. Действительно, если п - число верщин, то можно определить переменных Хц, j > t, 1 t, / п, следующим образом:

Xij = I, если элементы i и / находятся в различных модулях разбиения;

- Xij = О, если элементы i и / находятся в одном модуле. Пусть dj - число промежуточных соединений между элементами j и /, Wi - вес элемента i; вес необходим в силу того, что если некоторое множество компонент должно находиться в одном модуле (например, в триггере), то этот модуль представляется в виде элемента с весом, пропорциональным числу компонент. Минимизируемой функцией цели будет

Е СцХц. (i)

Ограничениями являются

JWiil - Xij)M для каждого / (2)

(т.е. ни один блок разбиения не может содержать модулей, общий вес которых превосходит М), и

YCijXijP для каждого / (3)

(ни один блок разбиения не содержит более Р выводов), и

Хц + Х1 + Х1 Ф1 (4)

для всех 1, /, к. (Неравенство (4) должно выполняться, поскольку если элементы i и k принадлежат разным блокам, то и элементы/и й и/или элементы/и^должны быть в разных блоках.)

Для графа с п вершинами число переменных равно (2)

а число ограничений равно 2п-\- g). Существующие методы

решения задач целочисленного математического программирования позволяют получить численное решение только для задач относительно малой размерности. Что касается разбиения схем с многооконечными сетями, то оно сводится к значительно более трудной задаче - задаче нелинейного программирования.

7.3.3. ОПТИМАЛЬНОЕ РАЗБИЕНИЕ С ДУБЛИРОВАНИЕМ ЭЛЕМЕНТОВ

Прежде чем закончить рассмотрение оптимальных решений задачи о разбиении, мы хотели бы указать на возможность применения дублирования элементов в случае, когда схема может

□

Рис. 7.6. Схема, предназначенная для разбиения.

На каждый внешний вход и внешний выход модуля, а также для каждой межмодульной сети, соединенной с данным модулем, требуется отдельный вывод. С каждым элементом связывается некоторое множество внешних сетей (для одиночного элемента все сети считаются внешними) 5 (или S (ej):

С каждым множеством элементов связывается множество внешних сетей, которые представляют собой соединения, ведущие к элементам других множеств. При этом множество S {Si, ef}, связанное с {е -, ej}, может и не совпадать с SlUS/. Например, S{e е^, e,} = {N, N, N, N, N}, но SUSgUS = {Л^1, Л^з, Л^4, Л^5. Л^б, Nt}. Это объясняется тем, что некоторые сети, являющиеся внешними для некоторых элементов множества, будут внутренними для всего множества элементов.

быть реализована таким образом, что некоторые ее элементы могут принадлежать нескольким модулям. Использование дублирования элементов представляет собой способ уменьшить число выводов за счет увеличения числа логических элементов схемы. Такой способ может быть экономически оправдан при современной технологии производства ИС.

Рассмотрим схему, изображенную на рис. 7.6 [30], на которой стрелками указаны направления передачи сигналов. Требуется разбить эту схему таким образом, чтобы каждый модуль содержал не более трех элементов и не более четырех выводов.

-I I г I

Модуль I

Модуль г

Рис. 7.7. Разбиение схемы с применением дублирования.

лирования существующих элементов. Например, схема, изображенная на рис. 7.6, может быть реализована на двух картах, как показано на рис. 7.7. Для каждой карты необходимо четыре вывода, два из которых являются соединениями между модулями. Заметим, что элемент ез присутствует в обоих модулях. Однако в модуле 1 этот элемент используется только для формирования входных сигналов элементов 64 и е^. Дублирование ез в модуле 2 использовано для образования входных сигналов элементов 64 и es. Таким образом, сети N5 и Ne становятся внутренними для обоих модулей. Дублирование элемента ез позволяет уменьшить на два необходимое число выходов модуля 1 и соответственно число входов модуля 2. В настоящее время не существует систематического метода получения оптимальных покрытий в случае использования дублирования. Тем не менее если у элемента схемы е^ есть входные сети ...,/ и выходные сети Оь ..., Ор и возможно его дублирование в следующем модуле, то выходы, соответствующие Оь ..., Ор, могут быть заменены выходами, соответствующими /ь ... , / , при соответствующей замене входов следующего модуля. Таким обра-

Однако справедливо, что S U S (е^) U S (е/). Для рассматриваемой схемы не существует допустимых множеств, содержащих по два или более элементов. Следовательно, для любого разбиения этой схемы требуются по крайней мере пять модулей и 18 выводов.

Эта схема иллюстрирует случай наличия существенных ограничений на число выводов в схеме в том смысле, что даже при увеличении разрешенного числа элементов в модуле множество допустимых объединений элементов в силу указанных ограничений не изменится. Для подобных схем иногда представляется возможным уменьшение числа выводов схемы путем введения дополнительных (необязательных) элементов, т. е. за счет дуб-

зом, каждый элемент определяет эквивалентность между различными множествами сетей. Задача о покрытиях может быть обобщена на основе рассмотрения эквивалентных множеств сетей, определяемых как множества сетей, связанных с данным множеством элементов.

Для схемы, изображенной на рис. 7.6, S{ei, ez, e) - - {Ni, N2, Ns, Ni, N5, Ne}. У элемента вз есть две входные сети N3 ц Ni и две выходные сети Л/5 и Ne. Следовательно, если элемент вз можно дублировать в (последующих) модулях, для которых N5 и Ne являются входами, мы сможем заменить выходные сети Л^5 и Ne на сети N3 и N4 и получить, таким образом, S{ei, 62, 63} = {N1, N2, N3, Ni}. Аналогично если ез содержится и в предшествующем модуле, то 8{ез, ei, £5} = {N3, Ni, N5, Ne N7, Ns} можно преобразовать в {N3, Ni, Nt, Ns}, что приводит к реализации, показанной на рис. 7.7.

7.4. РАЗБИЕНИЕ, МИНИМИЗИРУЮЩЕЕ ЧИСЛО СОЕДИНЕНИИ. СУБОПТИМАЛЬНЫЕ РЕШЕНИЯ

В настоящее время не существует методов решения задачи о разбиении, которые давали бы оптимальные решения в случае больших схем и были бы приемлемы с точки зрения объема вычислений. Поэтому представляется интересным рассмотреть эффективные методы получения субоптимальных решений. Такие процедуры позволяют получить несколько субоптимальных решений и затем выбрать из них наилучшее. Этот подход оправдан следующими соображениями. Обычно получение точного решения не является столь важным. К тому же при минимизации числа промежуточных соединений приходится учитывать различные ограничения на разбиение, которые иногда не могут быть сформулированы в точной математической форме. После того как найдено несколько субоптимальных решений, выбирается одно из них, удовлетворяющее требуемым ограничениям. При этом для получения оптимального решения зачастую требуется произвести большой объем вычислений, в то время как методы поиска субоптимальных решений быстро дают требуемый результат. (Следует отметить, что поскольку для графа с п вершинами объем вычислений при использовании данной процедуры возрастает много быстрее, чем п^, то ее практическое использование в случае больших схем нецелесообразно.)

7.4.1. ИТЕРАТИВНАЯ ПРОЦЕДУРА РАЗБИЕНИЯ

Рассмотрим задачу разбиения графа, содержащего 2п вершин, на два непересекающихся подмножества, содержащих точно по п вершин, с тем чтобы минимизировать число соединений

между этими двумя подмножествами. Ценой разбиения назовем число соединений между подмножествами.

Рассмотрим произвольное разбиение множества S, состоящего из 2п вершин, на два подмножества Bi и Bz, содержащих по п вершин. Кроме того, предположим, что Bj и Л* являются подмножествами s, которые определяют искомое разбиение, минимизирующее число соединений между подмножествами. Тогда существуют подмножества х^б F S Вг, такие, что iZ = F = n/2 (где ixi -число элементов множества X) и замена X на y дает В\ и В* соответственно. Это означает, что

b;==(b,-x)uf, b;{b-y)ux или b; = (B2-f)ux, в;=

= (В, - Xy\jy. Для определения В* и В* нам достаточно, таким образом, найти X н y. Наша стратегия поиска будет заключаться в том, чтобы отыскать подмножества Xi и Fi, содержащие р элементов Вх и р элементов Bg соответственно, такие, что замена Х\ на F, уменьшает цену разбиения, и замена любых других множеств Х\, F* (где x* = F*<p) не приведет к уменьшению цены разбиения. (Это, по существу, означает, что мы меняем местами множества, состоящие из малого числа элементов, получая локально оптимальное разбиение.) Уже при р = I время вычислений данной процедуры пропорционально (так как число перестановок п одиночных элементов равно ti, поэтому мы рассматриваем только случай р = 1. Процедура состоит в выборе произвольного исходного разбиения и последовательных перестановок одиночных элементов обоих множеств локально оптимальным образом до тех пор, пока возможно уменьшение цены результирующего разбиения. Мы принимаем ту локально оптимальную стратегию обмена местами пары элементов, которая обеспечивает наибольшее уменьшение цены.

Пример 7.1. Пусть для изображенного на рис. 7.8 графа исходное разбиение состоит из Bj = (1,2,3,4}, Вг = {5, 6, 7,8}. Перестановкой одиночных элементов, дающей наибольшее уменьшение числа соединений, является перестановка элементов 4 и 5, приводящая к разбиению В[ = {1, 2, 3, 5}, В2 = {4, 6, 7, 8}. При исходном разбиении было 5 соединений. После перестановки их стало 4. На этом шаге уже нет перестановки одиночных элементов, приводящей к дальнейшему уменьшению числа соединений, и, таким образом, прецедура заканчивается.

Теперь возникает вопрос, можно ли улучшить результаты этой процедуры путем использования перестановок одиночных элементов, которые сами по себе не приводят к изменению числа соединений. (В примере 7.1 элементы 2 и 6 из BI и Вг могут быть переставлены без изменения числа соединений.)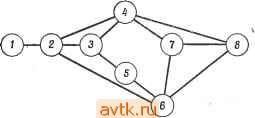

Рис. 7.8. Граф, предназначенный для разбиения.

рыш для всей схемы окажется нулевым. Однако среди всех полученных разбиений мы можем выбрать одно, имеющее наименьшее число соединений.

Пример 7.2. Рассмотрим исходное разбиение (12367, 458910) графа, изображенного на рис. 7.9. При таком разбиении число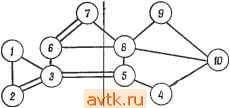

Рис. 7.9. Граф из примера 7.2.

соединений равно четырем. Оптимальным является обмен одиночными элементами 5 и 7, что действительно увеличивает число соединений. Результирующее разбиение, иллюстрируемое на рис. 7.10, а, имеет пять соединений, в то время как при исходном разбиении их было только четыре. Однако повторение процедуры позволяет получить из разбиения (12356, 478910) путем взаимной перестановки элементов 4 и 6 разбиение, при котором число соединений равно только трем, что показано на рис. 7.10, б.

Теперь можно сформулировать полную процедуру разбиения графа с 2п вершинами на два равномощных подмножества, минимизирующую число соединений.

Действительно, решения, получаемые при помощи этой процедуры, могут быть улучшены, если переставлять местами пары элементов, даже если эффект от их перестановки отрицателен, до тех пор, пока не будут переставлены все элементы. (Для предотвращения зацикливаний ни один элемент не переставляется более одного раза.) На этом этапе, как очевидно, выиг-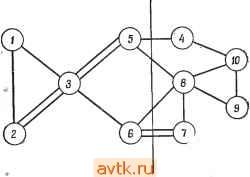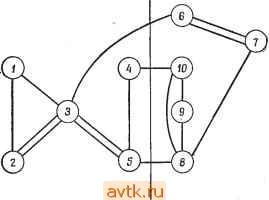

Рис. 7.10. Разбиение заданного графа.

2. Для каждой из пар элементов с е Bi, bBz подсчитываем уменьшение числа соединений, получаемое при перестановке местами а и Ь. Меняем местами ту пару элементов, для которой это уменьшение максимально по абсолютной величине (даже если его величина отрицательна). Если таких перестановок несколько, то выбираем любую из них.

3. Повторяем шаг 2 для каждых о е Bi и b Bz, которые еще не переставлялись, до тех пор, пока все элементы не при-

Процедура 7.1. (Кернихан -Лин [18])

1. Выбираем исходное разбиение (полученное произвольно или каким-то специальным образом) множества, состоящего из 2л вершин, на два непересекающихся подмножества Bi и Bz, состоящих из п вершин каждое.

мут участие в перестановках. Затем выбираем из всех образованных разбиений такое, которое содержит наименьшее число соединений.

Эффективность приближенного метода определяется следующими двумя факторами: 1) насколько хороши полученные с его помощью решения и 2) насколько большой объём вычислений при этом потребовался. Первый фактор может быть оценен на основе эмпирических результатов путем сравнения с другими методами. Однако второй фактор, который мы назовем сложностью, часто может быть (приближенно) оценен аналитически. Анализ сложности приближенных методов решения задач физического проектирования представляет определенный интерес.

Далее мы оценим сложность процедуры 7.1. Для схемы с 2п вершинами шаг 2 должен быть повторен п раз. Число возможных пар для (t+ 1)-й перестановки равно

{n-ir.

Следовательно, если рассматирвается каждый вариант перестановки, сложность этой эвристической процедуры будет пропорциональна по крайней мере rfi для больших п.

Однако для схем, содержащих только двухоконечные сет, целесообразные перестановки могут быть определены более простым способом. Для исходного разбиения на два множества Bi и Вг обозначим через число (внешних) соединений между элементом а е Bj и элементами Bg, а через - число (внутренних) соединений между а и другими элементами Вь Тогда Еп- £ fab, г'Де Саь' ~ число соединений между эле-

ментами а и Ь', и 7= V С^а', где Саа' определяется ана-

а' е В,

логично СаЬ' И С^а'- ПуСТЬ Da = Ea - la- Da ЯВЛЯСТСЯ МСрОЙ

уменьшения числа соединений в результате перенесения элемента а из Bi в Вг.

Следующие леммы позволяют выразить уменьшение числа соединений и значение. для хф а,Ь после перестановки элементов aBi и bBz как функцию этих значений до указанной перестановки.

Лемма 7.2. Уменьшение числа соединений в результате перестановки элементов се Bi и bBz определяется как gab =

= Da + Db - 2Cab.

Доказательство. Все внутренние соединения, ведущие к элементу а, за исключением соединений, ведущих к элементу Ь, становятся внешними, и наоборот. Аналогичное утверждение справедливо и для соединений, ведущих к элементу Ь. Соединения между а VI b остаются внешними. Следовательно, в результате перестановки местами элементов- а к Ь достигается умень-

шение числа соединений на ({Еа - Саь) - а) + ({Еь - Саь) -

-1ь) z= (Еа - 1а) + (Еь - h) - 2СаЬ = + Db - 2Cab gab.

Лемма 7.3. После перестановки элементов а е Bi и b новое значение D (обозначенное через D) определяется из следующих уравнений:

; = . + 2С -2С для х^В„ Dy-D-2C,-2C для у^В^.

Доказательство. Предлагается в качестве упражнения.

Для схем,-содержащих сети, имеющие только два выходных зажима (двухэлементные сети), шаги 2 и 3 процедуры 7.1 можно изменить.

2. Для каждых а^Ви b Bz вычисляем Da, Оь. Заменяем пару элементов, имеющую максимальное значение gabs. Вычисляем новые значения D для не переставленных ранее элементов. (Заметим, что это необходимо только для элементов, связанных с элементами а и/или Ь.) Повторяем шаг 2 до тех пор, пока возможны перестановки, и выбираем разбиение с наименьшим числом соединений.

Если в Bi и Bz значения D упорядочены по возрастанию, т. е. {Da >Da,> - --> Da) И (Db, Db> ... > DbJ, TO можно не рассматривать все возможные пары элементов. Можно сначала менять местами элементы, которые имеют относительно большие значения D. Если при просмотре множества D мы дошли до парыDa, 1)ь^,такой, что D. + Оь. <Da + Оь - Саъ^;

где Gm, bp - уже рассмотренная пара элементов, то не существует пары афи ki, / /, дающей лучший результат, чем перемена местами элементов а^ и bp. Поэтому для определения наилучшего результата надо рассмотреть только несколько пар. Можно показать, что время, необходимое для сортировки, возрастает как niogn, в силу чего общее время работы алгоритма возрастает как n4ogn [18].

Процедуру 7.1 можно обобщить на схемы с сетями, содержащими много выходных зажимов, следующим образом. Пусть для исходного разбиения В* обозначает число сетей, которые соединяют один или несколько элементов множества Bz с элементом а множества Bi. Аналогично/J-число сетей, соединенных с элементом а и не соединенных с элементами Bz (т. е. число внутренних сетей Bi, соединенных с а), и D* =£* - /*.

Пусть Са*ь* - число соединений (сетей) между элементами а множества Bi и между элементами b множества Bz, которые не соединены с другими элементами Bi или Bz. (Это как раз число сетей, имеющих два зажима и соединяющих элементы а и Ь.)