УПРАЖНЕНИЯ

6.1. Докажите, что может быть разработана универсальная древовидная структура УЛМ, требующая 2 -*-- -1 выводов для входных сигналов.

6.2. Используйте изображенный на рис. 6.6 УЛМ для реализации следующих функций шести переменных:

а) Si, 3, ъ(Х\, Хг, Хз, Xi Хъ, Хе),

б) f(Xi, ..., Лб) = 1 в том и только в том случае, если Xi-\-2хг-\-хз-\-+ 2.1:4 + ъ + 3-V6 4; сложение и умножение арифметические.

6.3. Определите модульную реализацию для каждого из следуюших последовательностных автоматов:

а) используя модули, изображенные на рис. 6.6,

б) используя модули, изображенные на рис. 6.8.

Рис. 6.40. К упражнению 6.3.

Рис. 6.41. К упражнению 6.4.

6.4. Определите модульную реализацию последовательностного автомата изображенного на рис. 6.41, используя модули на 5 входов (как в примере 6.5) и разбиения:

а) (123, 456);

б) (145, 236).

в) Можете ли вы определить разбиение, которое привело бы к более экономичной реализации?

г) Есть ли какая-нибудь связь между разбиениями, обладающими свойством подстановки, и хорошими разбиениями?

35. Weiner Р., Hopcroft J. Е., Bounded Fan-in, Bounded Fan-out Univorm Decompositions of Synchronous Sequential Machines, Princeton University Report, 1968.

36 Willies M. v.. The Best Way to Design an Automatic Calculating Machine, Manchester University Сотр. Inaugural Conference Report, pp. 16-18, July 1951.

37. Yau S. S., Tang C. K., Universal Logic Circuits and Their Modular Realizations, Proc. AFIPS Spring Joint Computer Conference, pp. 297-305, 1968.

38. Yau S. S., Tang C. K.., Universal Logic Modules and Their Applications, IEEE Trans, on Computers, vol. C-19, pp. 141-149, February 1970.

39. Yoeli M., Turner J. В., Decompositions of Group Functions with Applications to Two-Rail Cascades, Rept. SRI Project 5876, AFCRL 66-472. Stanford Research Institute, 1966.

6.5. Используйте матрицу Акерза дли реализации сЛеДуЮЩих функций:

а) xiQxz&xsΞ

б) 8г. s(xu Хг, Хз, Xi);

в) f(Xi, Xz, Хз, Xi)=\ тогда и только тогда, когда л;1 + 2л:2 + Зх:з+ + 4Xi 5;

г) g{Xl, Х2, Хз, Ai) = Х1Х2 + ХгХз + X3X1, + Х\Х .

6.6. Для каждой из функций задачи 6.5 определите реализацию каскада с двойными связями, используя при этом основной э,пемент, изображенный на рис. 6.22.

6.7. Для последовательностных автоматов задачи 6.2 определите реализацию с помощью итеративной матрицы.

6.8. Для функций задачи 6.5 определите слова, которые необходимо запомнить при реализации с использованием ассоциативной памяти. Для каждого случая необходимо определить, что будет дешевле: иметь три входных значения (О, 1, -) или только два значения (О, I)?

Часть III

Смежные вопросы: физическое проектирование И моделирование

Глава 7 ЗАДАЧИ

ФИЗИЧЕСКОГО ПРОЕКТИРОВАНИЯ

7.1. ВВЕДЕНИЕ

В предшествующих главах рассматривались различные задачи, возникающие при логическом проектировании цифровых схем. После завершения логического проектирования эти схемы реализуются на подложке или на плате (которые мы будем называть общим термином карта ). Каждая карта может содержать не более некоторого максимального числа элементов, поэтому оказывается необходимым разбиение схемы на подсхемы. Соединения между картами, их входы и выходы осуществляются через выводы соответствующих карт. Однако из-за того, что максимальное число выводов карты ограниченно, соединение их между собой оказывается более дорогостоящим, чем соединение элементов в пределах одной карты. Таким образом, одной из задач разбиения схемы является минимизация числа соединений между картами, что соответствует минимизации числа выводов карт.

После того как произведено разбиение схемы, должно производиться размещение ее элементов на картах и трассировка соединений между ними. При этом необходимо учитывать целый ряд ограничений. Для печатных плат одним из таких ограничений является планарность схемы (отсутствие пересечений между ее ветвями).

Задачи, которые должны быть решены на этапе проектирования схемы, назовем задачами физического проектирования. При современной технологии производства интегральных схем (ИС) к таким задачам относятся:

1. Разбиение схемы на функциональные части (подсхемы).

2. Выбор из наличного множества ИС, использующихся для реализации каждой подсхемы, и назначение каждому элементу схемы его части выбранной ИС.

3. Разбиение выбранного множества ИС на подмножества, которые затем распределяются по картам.

4. Размещение ИС на выделенных для них картах.

5. Установление соответствия между выводами ИС, выводами карт и конкретными сигналами.

6. Трассировка соединений между ИС, находящимися на одной карте.

7. Размещение всех карт на несущей плате.

8. Определение соединений между картами на одной несущей плате.

При рещении этой задачи рассмотреть все варианты рещения невозможно. Например, для размещения М ИС на карте, имеющей позиций [NM), существуют М! j вариантов возможных размещений. Рассмотрение всех вариантов допустимо только для малых значений N к М. При этом во многих задачах такого рода сам критерий оценки нельзя сформулировать в четкой математической форме, в силу чего часто используются субоптимальные целевые функции. Таким образом, хотя истинной целью выбора варианта размещения карт является упрощение последующей трассировки карт, на практике часто используется субоптимальная целевая функция, например минимум общей длины соединений.

По этим причинам обычно не ищут оптимальных решений вышеуказанных задач, а вместо этого разрабатывают эффективные процедуры, направленные на получение приемлемых решений на основе субоптимальной целевой функции. Такие процедуры называют иногда эвристическими. На основе нескольких эвристических решений или повторного использования одного из них можно получить различные варианты субоптимальных решений, соответствующих различным целевым функциям. Эти варианты могут затем детально исследоваться для определения лучшего из них по отношению к истинному оптимуму. В идеальном случае всю эту последовательность задач можно рассматривать как одну общую задачу. Однако практически это обычно невозможно из-за больших размеров рассматриваемых схем. В этой главе мы рассмотрим некоторые полезные процедуры, разработанные для различных задач разбиения, размещения и трассировки, встречающихся при компоновке цифровых систем.

7.2. ГРАФЫ СХЕМ

Для решения многих задач, возникающих при реализации схем, удобно ввести в рассмотрение графы. Граф имеет узлы (вершины) и ребра (дуги), в то время как схема состоит из элементов (ими могут быть ИС) и связывающих их соединений, образующих так называемуюсыгналньг;/о сеть (или просто сеть),

соединяющую два или более элементов. Естественным является представление отдельных элементов схемы верщинами, а соединений дугами графа. Например, схеме, изображенной на рис. 7.1, а, соответствует граф, изображенный на рис. 7.1,6.

При таком подходе не возникает осложнений, в случае когда сеть может соединять между собой только два элемента в силу того, что дуга графа соединяет между собой также две верщи-ны. Сложности возникают при представлении схем в виде графов, в которых одна сеть связывает между собой более двух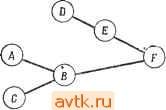

Рис. 7.1. Схема и ее графическое представление.

элементов (т. е. в случае, когда коэффициент разветвления превосходит 1). В качестве примера можно привести изображенную на рис. 7.2,а схему, в которой четыре элемента-Л, В, С и Е - соединены между собой одной общей сетью. Сеть, связывающая между собой более двух элементов, называется многоэлементной или многооконечной. Схеме, содержащей такие соединения, можно поставить в соответствие гиперграф, т. е. обобщенный граф, каждое ребро которого может соединять между собой более двух вершин [24]. Однако большинство теоретических результатов, полученных в области теории графов, приложимы только к регулярным графам, т. е. к графам, в которых ребро соединяет между собой только два узла. В настоящее время известно несколько методов построения графов для схем

ветствие

ребер, каждое из которых соединяет только два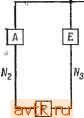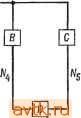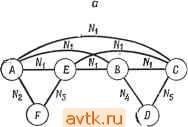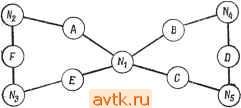

в

Рис. 7.2. Многоконечная сеть и ее графическое представление.

элемента. На рис. 7.2,6 представлен такой граф, соответствующий схеме, изображенной на рис. 7.2, а. Сеть Nu которая связывает между собой сразу четыре элемента, представлена на этом графе шестью соответственно отмеченными ребрами.

Другой метод представления схем, содержащих многооконечные сети, основан на представлении в виде вершин графа

произвольного вида. Один из этих методов основан на том, что сети, связывающей между собой N элементов, ставится в соот-

как самих элементов, так и соединений схемы. Такой граф называют двудольным или биграфом, поскольку его вершины можно разделить на два непересекающихся подмножества: подмножество вершин, соответствующих элементам, и подмножество вершин, соответствующих соединениям схемы; при этом все ребра графа соединяют между собой элементы, принадлежащие разным подмножествам.

Ни один из описанных выше методов представления многооконечных сетей при помощи регулярных графов не обеспечивает непосредственного соответствия графа реальной схеме. В силу этого необходимо проявлять особое внимание при использовании графов для решения задач, связанных с физической реализацией схем с многооконечными соединениями. Так, схему, изображенную на рис. 7.2, а, можно, как это показано на рисунке пунктирной линией, разбить на две части, связанные только одной сетью. В то же время осуществить такое разбиение на основе графов, изображенных на рис. 7.2,6 и в, нельзя. Для исключения подобных несоответствий необходимы надлежащие модификации указанных процедур. Можно использовать и другие процедуры поиска приближенных (т. е. не оптимальных) решений.

7.3. РАЗБИЕНИЕ, МИНИМИЗИРУЮЩЕЕ ЧИСЛО СОЕДИНЕНИЙ. ОПТИМАЛЬНЫЕ РЕШЕНИЯ

В этом параграфе будут рассмотрены процедуры получения оптимальных решений задачи о разбиении схем при минимизации числа соединений между блоками (модулями).

7.3.1. СВЕДЕНИЕ К ЗАДАЧЕ О ПОКРЫТИИ

Один из вариантов задачи о разбиении может быть сформулирован как классическая задача о покрытии. Предположим, что требуется разместить множество взаимосвязанных элементов в отдельных модулях, обеспечив минимальное число соединений между модулями, так чтобы ни один из модулей не содержал более некоторого максимального числа элементов М и числа соединений Е. Множество элементов Т является допустимым, если его элементы могут быть размещены в одном модуле без нарушения указанных ограничений (т. е. число элементов в Т не превосходит М и число электрических соединений, связывающих между собой элементы Т, не больше Е). Набор допустимых множеств Tl, Т2, ..., Тр определяет возможное покрытие, если каждый элемент содержится по крайней мере в одном множестве. (Мы не требуем выполнения условия, чтобы каждый элемент содержался только в одном множестве по причинам.

которые будут объяснены ниже.) Если n(Ti) -Число соединений, соответствующее множеству элементов Ti, то число соединений

р

между множествами (Т^Тг,... ,Тр) будет равно zl ti{Ti) - щ,

где tit - общее число различных соединений схемы. (Предлагается доказать самостоятельно.) Оптимальное покрытие является, таким образом, допустимым покрытием, которое мини-р

мизирует /] n{Ti).

Пусть имеются два допустимых множества элементов Ti и Гг. Говорят, что Ji доминирует над Гг, если Гг с= Г, и n{Ti)== п(Гг). Следующая лемма показывает, что оптимальное покрытие может быть выбрано из совокупности допустимых множеств, над которыми не доминирует ни одно другое допустимое множество.

Лемма 7.1. Для любой схемы С существует оптимальное покрытие (Гь Гг, ..., Тр), в котором над Ti, i - I, ..., р, не доминирует ни рдно другое допустимое множество элементов.

Доказательство. Предположим, что оптимальное разбиение содержит модуль, соответствующий множеству элементов Ti, и над Ti доминирует другое допустимое множество Tj. Замена Тг на Tj приводит к другому оптимальному разбиению. Это рассуждение можно повторять до тех пор, пока не будет получено искомое разбиение.

Из леммы 7.1 следует, .что мы можем рассматривать в качестве модулей только те множества элементов, над которыми не доминирует никакое другое множество, что упрощает нашу задачу. Рассмотрим схему, представленную биграфом, изображенном на рис. 7.3, с элементами и сетями Ni и попытаемся разбить эту схему при ограничениях М 4, £ 4.

Если Tl и Гг являются множествами, такими, что Ti а Гг, то (Гг) n{Ti). Тогда если Ti не является допустимым, то и Гг не является допустимым. Следовательно, возможно получить все допустимые множества путем объединения меньших множеств. Если не существует допустимых множеств, содержащих по k элементов, то не существует и допустимых множеств, содержащих по k> k элементов. Обозначив через Si множество сетей, связанных с элементом е мы получим следующие множества сетей изображенной на рис. 7.3 схемы:

Si=-{Ni, N N,},

SziNi, N N,},

S3 = {/V4, N N,},

S,={N N N,},

Sb = {N N N,}, . S,= {N N N- N,}.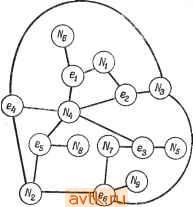

Рис. 7.3. Биграф, представляющий схему.

Существенная информация может быть сведена в таблицу, аналогичную таблице покрытия простых импликант, строки которой представляют допустимые множества Ti и соответствующие им цены п(Т{), а столбцы представляют элементы схемы. Наличие единицы на пересечении t-й строки и /-го столбца показывает, что gj принадлежит множеству Г,. Минимальным покрытием называется множество строк, которые содержат все элементы (покрывают все столбцы) и имеют минимальную цену. Такое покрытие может быть построено на основе метода ветвей и границ и метода доминирования. На рис. 7.4 представлена таблица покрытий для изображенной на рис. 7.3 схемы. Для этого примера минимальное покрытие состоит из множеств {61,62}, {63}, {64,65}, {ее}. Число соединений между ними равно 2п(Гг) - П( =;= 15 -9 = 6. Полученное разбиение показано па

При эком допустимыми множествами, состоящими из двух элементов, являются

SiUS.iNz, N3, Ni, N,}.

Так как не существует допустимых множеств из трех или более элементов, то для всех таких множеств число сетей больще четырех. Из леммы 7.1 следует, что оптимальное разбиение может быть выбрано из следующего набора допустимых множеств элементов: {ei}, {62), {ез}, {ei}, {е^}, {ев}, {еь eg}, {£2,64}, (64,65}-

Рис. 7.4. Таблица покрытия для задачи о разбиении.

Рис. 7.5. Разбиение схемы.

смотрим граф, содержащий пять верщин, и связанную с ним сеть:

Si = {Nu n2}, 82 = {n2, N,},

Предположим, что рассматриваемую схему надо разбить при ограничениях М 3, Е 4. Недоминируемыми допустимыми множествами являются: {ei}, {ег}. {з}, {64}, {es}, {ь 62,3}. {ь 4, eg}. Минимальное покрытие, выбранное из этих допусти-

рис. 7.5. Минимальное покрытие может иметь один или' более элементов, содержащихся более чем в одном множестве. Рас-