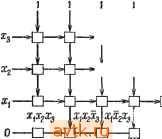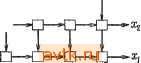XfX ijijig XfCx щхз з:,!, -О-D-□-D-f

Рис. 6.23. Реализация комбинационнной функции при использовании матрицы на элементах одноразрядного сумматора, пример 6.8

минтермов. Порядок, в котором получаются минтермы в матрице п X 2 , может быть определен следующим образом: пусть входные сигналы х элементов первого столбца будут обозначены сверху вниз как Хп, Хп-и - лгг, Х\ и пусть столбцы будут обозначены как О, 1,...,2 -1 слева направо. Выходом столбца /, О / 2 - 1, является т^п . . Например, если п = 3, то выходом пятого столбца является минтерм == XiXzXs, а выходом четвертого столбца является минтерм тз = xxzXg.

Другой тип итеративной матрицы, который может быть использован для реализации любой комбинационной функции, предложен Акерзом [1]. Типовой элемент матрицы имеет три входных сигнала х, у и z я два выходных и 0. Входы х и у каждого элемента соединяются с выходами элемента х и у, находящегося соответственно слева и сверху от него, как в ранее рассмотренном примере, а вход z управляется извне. Выходы и 0 каждого элемента реализуют одну и ту же функцию, показанную в таблице истинности на рис. 6.24.

Выходные сигналы элемента при л; = О, у = I не определены. Определим граничные условия матрицы таким образом, чтобы эти две входные комбинации никогда не подавались ни на один элемент матрицы, т.е. чтобы входы любого элемента

коллектором в том и только в том случае, если f для соответствующего минтерма должна быть равна единице. Функция / получается на горизонтальном выходе элемента, находящегося в нижнем правом углу. Размер матрицы для реализации функции п переменных равен (п + 1)Х2 .

Пример 6.8. Реализация функции f-xXz + XiXs на итеративной матрице с использованием элементов полусумматора, представленных на рис. 6.22, показана на рис. 6.23. Минтермами функции являются xiXzXs, Х1Х2Х3 и X1X2XZ. На рис. 6.23 также изображены те выводы матрицы, на которых получается каждый из

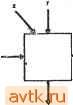Рис. 6.24. Основной элемент матрицы Акерза.

каждого элемента удовлетворяют условию у х = у х независимо от значения входных сигналов z матрицы. Таким образом, условие использования элементов, показанных на рис. 6.24, удовлетворяется всеми элементами матрицы.

При использовании прямоугольной матрицы для реализации произвольной комбинационной функции необходимо произвести соединение всех входов х первого столбца с константой 1 и всех входов у верхней строки с константой 0. Входы цепи должны быть соединены со входами z элементов, а выход должен сниматься с элемента, находящегося в правом нижнем углу матрицы. Матрицу подобного рода можно построить при наличии, с одной стороны, логических схем с фиксированным числом межэлементных соединений и - с другой, при наличии метода подсоединения входных сигналов к соответствующим элементам.

Поскольку входные сигналы х и у на границах матрицы всегда зафиксированы на одном значении, то задание входа матрицы может быть представлено входами z каждого элемента матрицы, как показано на рис. 6.25. Для определения выход-

удовлетворяли условию у х. При выполнении этого условия типовой элемент может реализовать любую из следующих четырех функций: 1) ху + yz-\-XZ, 2) x{y-\-z), 3) xz + yz, 4) у-f -f- xz. Нижеследующие рассуждения справедливы ко всем четырем типам указанных выше элементов.

Рассмотрим прямоугольную матрицу таких элементов, в которых все входные сигналы х первого столбца равны 1, а входные сигналы у элементов верхней строки равны 0. Можно показать, что при этих условиях входные и выходные сигналы

Рис. 6.25. Вид входных сигналов матрицы.

Подобным же образом, если входной сигнал элемента (1,1) равен О, то выходные сигналы всех элементов верхней строки будут равны О и эту строку можно исключить. Таким образом, выходной сигнал матрицы может быть определен последовательным исключением строк и столбцов в зависимости от значения входного сигнала z, поданного на элемент, расположенный в левом верхнем углу оставшейся части матрицы. Выходной сигнал будет равен 1 в том случае, если последним исключен столбец, и равен О, если последней исключена строка. Если столбцы и строки обозначить соответственно через С и то исключение столбцов и строк матрицы, изображенной на рис. 6.25, будет происходить в следующем порядке: С1, /?1, С2, СЗ, i?2, С'4, /?3, С5, Сб. Последним был исключен столбец 6, и, следовательно, выходной сигнал элемента правого нижнего угла равен 1. Отметим, что эта простая процедура определяет выходные сигналы всех элементов матрицы.

Пусть запись 2гу означает входной сигнал z элемента i-й строки и /-Г0 столбца матрицы m X Множество входных сигналов 2;Z[ , z, z , значения которых равны О и которые удовлетворяют условию /1/2... /т, называется 0-траекторией. Аналогично множество сигналов z

НОГО сигнала цепи для заданной комбинации входных сигналов Z может быть использован простой метод.

Рассмотрим элемент матрицы, относящийся к элементу (1,1) таблицы (левый верхний угол). Если входной сигнал z этого элемента равен 1, то выходные сигналы элемента будут равны 1. Поскольку каждый элемент первого столбца имеет на входе X сигнал, равный 1, то выходные сигналы всех элементов этого столбца будут равны 1. Следовательно, все элементы второго столбца будут иметь на входе х сигнал, равный 1. Выходной сигнал матрицы не изменится, если убрать первый столбец.

, имеющих значение! и удовлетворяющих условию tl

12 ... г'п, называется 1-траекторией. Из рассмотренной выше процедуры исключения столбцов и строк следует, что при некоторой входной комбинации выходным сигналом матрицы будет 1 в том и только в том случае, если существует 1-траектория матрицы для этой входной комбинации. Аналогично, для того чтобы выходным сигналом матрицы был О, необходимо существование 0-траектории для входной комбинации.

Матричная реализация любой комбинационной функции может быть получена с помощью следующей процедуры, если в качестве основного используется именно этот элемент.

Процедура 6.3

1) Получаем сумму произведений и произведение сумм выражений функции f, которая должна быть реализована.

2) Строим таблицу, строки которой отвечают произведениям Рг выражения суммы произведений, а столбцы отвечают суммам Sj выражения произведения сумм. Элементом {i, j) таблицы является любой входной литерал такого же вида, какой имеется и в Pi, и в Sj. (Для любых Рг И Sj вссгда существует по крайней мере один такой литерал.)

3) Входной сигнал г элемента (i, j) матрицы совпадает с входным сигналом для элемента (i, /) сформированной на втором шаге таблицы.

Если входная комбинация, подаваемая на матрицу, соответствует точке 1 функции, то входные сигналы z всех элементов строки, представляющей соответствующее произведение, будут равны I. Это приводит к созданию 1-траектории и получению на выходе матрицы 1. Для реализации функции f матрица должна иметь единичный выход в том и только в том случае, если произведение Рг равно 1. Если поданная входная комбинация соответствует точке О функции, то по крайней мере одна сумма Sj будет равна 0. Это накладывает требование равенства нулю всех литералов суммы и создает 0-траекторию в матрице. Таким образом, процедура 6.3 приводит к реализации любой комбинационной функции. Размеры матрицы, однако, при этом могут быть не обязательно минимальными.

Пример 6.9. Рассмотрим функцию f - аЪс-\-abd-\-bed. Реализация ее в виде произведения сумм имеет вид / = = (P-f с) (й-f-&) (Ь-f d) (а-f fc + с). Для построения матрицы требуется 12 элементов, входы z которых заданы таблицей (рис. 6.26), полученной при использовании процедуры 6.3.

При построении таблицы, строки которой соответствуют точкам 1, а столбцы - точкам О, процедуру 6.3 можно модифицировать для получения матричной реализаций непосредственно

ИЗ таблиц истинности. Элементом таблицы (/, /) является любой литерал, имеющий значение 1 для точек 1, соответствующих 1-й строке, и значение О для точек О, соответствующих /-столбцу. Неопределенные элементы таблицы истинности не используются. Получаемые этим методом матрицы часто могут быть упрощены [2].

Рис. 6.26. Матричная реализация комбинационной функции, пример 6.9

Так же могут быть построены матрицы для реализации функции в виде компонентов подфункций. На рис. 6.27 показано, как могут быть получены схемы И и ИЛИ двух функций f\ и fz-

Рис. 6.27. Схемы И и ИЛИ для двух функций.

Пусть на рис. 6.27, а fi = fz - O. Часть fi будет содержать 0-траекторию, так же как и часть fz- О-траектория в /г не будет находиться слева, как в fi. Следовательно, комбинация образует 0-траекторию всей матрицы. Аналогично если либо fi, либо fa (или обе одновременно) равны 1, то вся матрица будет иметь 1-траекторию. Отметим, что строка с единичными входами, находящаяся непосредственно над fz, обеспечивает непрерывность 1-траектории от fu если f2 = 0. Те части матрицы, которые показаны пунктирными линиями, включаются только для того, чтобы сделать матрицу прямоугольной. Они могут быть опущены при обеспечении входов хну элементов на левой и верхней границах значениями 1 и О соответственно.

Матрица, представленная на рис. 6.27, б, будет иметь 0-траекторию, если fl или fa имеют 0-траекторию. Функции fi и /г должны иметь 1-траектории для того, чтобы полная матрица имела 1-траекторию. Таким образом, матрица реализует fifz.

Рис. 6.28. Реализация функции из ее компонентов-подфункций.

Продемонстрируем теперь, каким образом может быть реализована функция в терминах произвольных компонентов функций. Пусть f == abgi -f agz, где gi а-{-Ъс, a g2 = b -{-с. В виде произведения сумм функция f - (с -f Ь) X X (й -f gl) (g -f gz) Используя процедуру 6.3, получаем реализацию, показанную на рис. 6.28, g, для функций f, gl и gz. Матрицы для функций gl и 2 включаются в матрицу функции f, как показано на рис. 6.28, г, для получения окончательной реализации.

Верхней границей числа элементов, требуемых для реализации функции п переменных, является произведение числа точек 1 функции и числа точек 0. Таким образом, функция п переменных может потребовать максимум 2 -1 X 2 - = 2 элементов. Это значение может быть несколько улучшено при построении матриц, которые могут реализовать любую функцию п переменных. Рассмотрим матрицу 3X3 (рис. 6.29). Любая функция F{a,b,c) может быть записана как F(a, Ь, с) = &cfo + &cfi-f Ьс2+где /о = = Fia,Q,Q), fi = F(a.Q,\), h=F{a,\,()) и /з = /( , 1, 1).

Рис. 6.29. Универсальная матрица трех переменных.

Таким образом, fi = О, 1, а или а. Если Ь == с == О, то на рис. 6.29 будет существовать 1-траектория (fo - b - с), если fo=l; но если fo = 0, то таблица будет иметь 0-траекторию (c - fo - b). Следовательно, если b = с - О, то выходом матрицы будет fo-Следуя подобным рассуждениям, можно показать, что матрица на рис. 6.29 является универсальной матирцей трех переменных, поскольку она может быть использована для реализации любых функций трех переменных путем соединения соответствующих констант с элементами fi.

Рис. 6.30. Универсальная матрица четырех переменных.

Универсальная матрица для четырех переменных может быть построена путем использования двух матриц для трех переменных. Функция четырех переменных может быть выражена в виде F{a,b,c,d)=zdF{a,b,c,0)-\-dF{a,b,c,l). Каждая из функций F{a,b,c,b) и F{a,b,c,l) может быть реализована матрицей 3X3, как показано на рис. 6.29.

Объединяя две матрицы 3X3, как показано на рис. 6.30, получаем матрицу 5X5 (рис. 6.30), где функции f,-, О t 7, определяются так, как показано на рис. 6.29. Число элементов, необходимое для универсальной матрицы на п переменных, при использовании этого метода построения равно {2--\-1). Для упрощения соединений желательно иметь одну и ту же входную переменную для элементов диагонали матрицы. Для достижения этого входы элементов, отмеченные звездочкой, могут быть заменены с на с и с Я на с соответственно без изменения функции, реализуемой матрицей.

Хотя верхняя граница числа элементов, необходимых для реализации произвольных функций, превышает эту величину для универсальных матриц, однако для специальных классов функций может быть достигнута высокая эффективность реализации. Рассмотрим, например, матрицу, показанную на рис. 6.31. Легко убедиться, что выходным сигналом матрицы будет 1 в

ТОМ и только в том случае, если по крайней мере три входных сигнала будут равны 1. Следовательно, матрица реализует функцию 5з, 4,5 (а, b,c,d,e), равную 1 только в случае, если три или более входных сигнала будут равны 1. Аналогичная матрица с т столбцами и (п - т+ 1) строками, показанная на рис. 6.32, может реализовать цепь, имеющую единичное значение в случае, если т или более из ее п входных сигналов будут равны 1.

На рис. 6.32 изображена матрица, для которой требуется значительно меньшее число элементов, чем для универсальной матрицы, реализующая произвольную функцию того же числа переменных. Входные сигналы z элементов, располагающихся на диагонали матрицы, являются одной и той же переменной, следовательно, вид межэлементных соединений входов z также является типовым. Можно также предложить относительно про-

Рис. 6.31 Реализация матрицы Ss, 4.5 (а, Ь, с, й, е).

Рис. 6.32. Реализация матрицы Sm> .... и х^.

стые способы реализации пороговых функций с положительными весовыми коэффициентами и способы реализации симметричных функций.

6.3.3 ИТЕРАТИВНАЯ РЕАЛИЗАЦИЯ

ПОСЛЕДОВАТЕЛЬНОСТНЫХ АВТОМАТОВ

Итеративная реализация одинарных (двоичных) входных определенных событий может быть получена при использовании элементов одноразрядного сумматора с добавлением синхрони-

зированного D-триггера к выходу у каждого элемента. Если определенное событие рмеет порядок k, то используется матрица (п+ 1) Х2 и вход X автомата подсоединяется к элементам первых k строк первой колонки. Вертикальные выходы k строки будут являться минтермами последних k значений входного сигнала автомата. Таким образом, любое определенное событие k порядка может быть реализовано подсоединением соответствую-щих выходов k-\\ строки к строке-коллектору.

Пример 6.10. Рассмотрим определенное событие, представленное таблицей состояний на рис. 6.14, а и повторенное на рис. 6.33. Для того чтобы получить реализацию определенного события на эле- , * ментах одноразрядного сумматора, выразим сперва выход z{t) в виде функции последних входных сигналов. Используя обозначения примера 6.6, можно выразить выход таким образом:

2(0-246 (0 = (-l)i356 (-l) +

+ x(/-l)j/4(/-l).

Переменные yzze(t-\) и у^{1-\) могут быть теперь выражены через x{t - 2) и, возможно, некоторые другие переменные у. Поскольку таблица состояний представляет определенное событие четвертого порядка, процедура закончится выражением выходного сигнала как функции последних четырех значений только входного сигнала х. Окончательный результат имеет вид

z{t) = x{t - \)x{t - 2)x{t - Ъ) х{1 - 4) -\г x{t - \)x{t - 2) +

+ x{t-\)x{t-2)x(t-3).

Это выражение выходного сигнала через значение последних входных сигналов подразумевалось в процедуре древовидной реализации, использованной в примере 6.5. Задавая x{t--\), x{t - 2),x{t - 2,) и л;( - 4) как входные сигналы z(t) можно выразить в виде суммы следующих минтермов: mi, rrii, ms, me, mr, mio и mil, где наименьший значащий бит представляет x{t - 4). Определенное событие может быть реализовано матрицей 5X16, как и в случае комбинационных функций с четырьмя входными сигналами, за исключением того, что каждый элемент содержит £)-триггер и входной сигнал х подсоединяется к первым четырем строкам.

Любой последовательностный автомат, имеющий конечное состояние, может быть реализован в виде итеративной матрицы

Рис. 6.33. Таблица состояний для примера 6.10.

У

получением первоначально двоичной функции обратной связи, как это показано в гл. 5, и реализации затем выходной функции

и функции обратной связи путем использования итеративных матриц. Поскольку эти функции зависят от последних значений входных сигналов и функции обратной связи, основной элемент составляется как комбинация двух элементов одноразрядного сумматора, показанная на рис. 6.34. Каждый элемент содержит также /?-триг-гер задержки.

На рис. 6.35 показан общий вид реализации. Горизонтальные выходы последнего столбца каждой матрицы совпадают с горизонтальными входами первого столбца. Следовательно, эти выходы матрицы, реализующей функцию обратной связи /, могут быть соединены с матрицей, реализующей функцию выхода г, как показано на рисунке. Элементы того же типа используются в строке-коллекторе, хотя используется только один выход строки-коллектора. Как указывалось ранее, соединение со

a:jff

Рис 6.34. Основной элемент матрицы последовательностного автомата.

О-г

0-Lj-i

Т

,1 ,1

ОП:::::

Функция обратной связи Функция выхода

Рис 6.35. Матричная реализация последовательностного автомата.

строкой-коллектором производится в том и только в том случае, если созданный минтерм является точкой 1 для функции, реализуемой матрицей.