КИМ образом, что она будет давать реализацию в виде древовидной структуры, в которой выход каждого модуля (за исключением выходного модуля) имеет коэффициент разветвления по выходу, равный единице. Рассмотрим сначала определенные события, которые могут быть реализованы без контура обратной связи.

Как и в процедуре 6.1, начнем с модуля, соответствующего состояниям, которые дают на выходе единицу. Модули, соответствующие О- и 1-предшественникам этих состояний, соединяются

Рис. 6.14. Таблица состояний (а); древовидная структура модульной реализации (б), пример 6.5.

С выводами Ьо и Ь^. Процедура повторяется до тех пор, пока входы в последнее множество модулей не будут равны 1 и 0. После завершения процедуры получается реализация типа дерева в том и только в том случае, если таблица состояний представляет собой определенное событие. Можно показать (предлагается в качестве упражнения), что количество уровней в реализации равно количеству последних входных значений, которые определяют состояние автомата. Таким образом, fe-уровневое дерево модулей может быть использовано для реализации любого определенного события k порядка путем использования соответствующих констант на выходах Ъ и соединения входного сигнала х с выходом а всех модулей.

Пример 6.5. На рис. 6.14 показаны таблица состояний и ее модульная реализация типа дерева. Выходные сигналы заштри-

Рог

о

й

Рис 6.15.. Последовательностный модуль (й); схематическое изображение

модуля (б).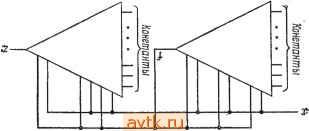

Рис. 6.16. Модульная реализация с коэффициентом обратной связи, равным

единице.

хованных модулей являются константами. (Эти модули показаны на рисунке для того, чтобы представить реализацию в виде завершенного дерева.)

В гл. 5 было показано, что любой синхронный последовательностный автомат может быть реализован с единственным контуром обратной связи. На основании этого покажем теперь, как любой автомат Мура может быть реализован при использовании модулей только одного типа, показанного на рис. 6.15, и типовой структуры в виде двух деревьев. Модуль является модификацией показанного на рис. 6.11 модуля для случая г = 2, т.е. двух двоичных сигналов х и f. Он реализует функцию у = booxf -\- boixf biixf -\- bioxj. Обший вид реализации показан на рис. 6.16, на котором каждый треугольник представляет дерево модулей. Входной сигнал х и выходной сигнал f первого дерева соединены с выводами х и f соответственно каждого модуля. Входные зажимы соединены с константами О и 1. Для получения реализации типа дерева для любого автомата Мура с одним двоичным входным сигналом может быть использована следующая процедура.

Процедура 6.2

1) Строим универсальный импликационный граф автомата, как это сделано в процедуре 5.3. Определяем функцию f{Q), которая исключает все замкнутые контуры. В отличие от процедуры 5.3 потребуем здесь, чтобы f{gi, Ij) - f{qi, Z) для всех Ij и /ft, иначе говоря, f определяется как функция, зависящая только от состояния автомата. Как отмечено в гл. 5, расщепление состояния может быть вызвано необходимостью разомкнуть все замкнутые контуры в импликационном графе.

2) Получаем расширенную таблицу состояний с входными сигналами х и f и состояниями Q. Элемент строки qi и столбца iXj,fk) указывает следующее состояние N{qi,Xj), если f{qi)=fh, и является неопределенным в случае f{qi)Фfk Расширенная таблица состояний будет содержать несколько неопределенных элементов, которые могут быть использованы для упрощения реализации. Это относится к таким комбинациям х, f и состоянию, которые не могут существовать.

3) Строим два дерева с входными сигналами х и f, одно из них для реализации функции обратной связи /, а другое для реализации выходной функции, используя ранее рассмотренную процедуру для определенных событий и модулей типа показанного на рис. 6.15.

Пример 6.6. Таблица состояний примера 6.1 повторена на рис. 6.17, а. Ее универсальный импликационный граф показан на рис. 6.17,6, а функция обратной связи f(Q) показана справа от таблицы состояний. Таблица на рис. 6.17, в показывает

следующее состояние в виде функции текущего состояния, входного сигнала и текущего значения f.

Обозначим выходной сигнал любого модуля через у с индексами, представляющими множество состояний, для которых выходной сигнал модуля будет равен 1. Тогда / = j/23, поскольку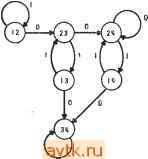

01 11

о

Рис. 6.17. Таблица состояний (а); универсальный импликационный граф (б); следующее состояние как функция х и (в) (пример 6.6).

f- 1 для состояний 2 и 3. По таблице рис. 6.17, е можно выразить следующее значение У23 в виде функции входных сигналов модуля

= Xfyi + Xfy.2 + Х/Уз + Xfyi.

Поскольку расширенная таблица переходов содержит неопределенные элементы, можно провести присвоение кодов таким образом, чтобы упростить реализацию. Например, 00-предшествен-никами состояний 2 и 3 могут быть состояния 1, 2 и 3, из которых два последних зависят от кодирования неопределенных следующих состояний в столбце 00 значениями 2 или 3. Такие возможные элементы заключим в круглые скобки. Тогда уравнение для F23 можно записать в виде

Y23 = Xfyi (23) + Х/J/2 (14) + X/j/3(!4) + Xfj/i (23),

Теперь можно получить функции, реализуемые модулями на следующем уровне. Например,

1(23) ~Уф{т) fУф(m] xfy2(m) ~ х^Уф(т)

где <р - пустое множество. Поскольку элементы внутри скобок не являются обязательными, можно переписать это уравнение в такой форме:

il(23)=f-О + х/-О + х/- 1+xf-0.

Это означает, что выводы boo, t>oi, Ьц и Ью модуля, реализующего Уи могут быть соединены с константами О, О, 1 и О соответственно. Подобным образом,

2(14) ~ #(234) ~ -2(134) Уф{т) -1(234)

3(14) - fVl (234) + Уф (134) + 3(124) + fУф ШУ

Поскольку все входы Ь, определенные этими уравнениями, могут быть реализованы как константы, то функцию обратной связи f можно реализовать посредством двухуровневого дерева, как показано на рис. 6.18. Такая же процедура используется для построения выходного дерева, начиная от г = 24- Полная реализация показана на рис. 6.18. Заштрихованные модули, выход которых остается неизменным, могут быть опущены, если нет необходимости представить завершенное дерево.

В некоторых частных случаях последовательностный автомат можно реализовать с помощью простого дерева. Если импликационный граф не содержит петель, то автомат представляет собой определенное событие и может быть реализован деревом с сигналами / = О или f - 1 или деревом из модулей на три входа, как указывалось ранее. Если выходная функция может быть использована как функция обратной связи для раскрытия всех петель в импликационном графе, то функция может быть реализована на основе дерева, в котором выходной сигнал г соединяется с выводами / всех модулей.

В древовидной структуре, рассмотренной выше, коэффициент объединения по входу каждого модуля фиксирован. Однако входной сигнал х и функция обратной связи f разветвляются на все модули. Ньюборн и Арнольд [22] разработали модули и технологию синтеза, которые дают модульную реализацию с фиксированным коэффициентом разветвления по выходу. На рис. 6.19 показан модуль, который можно использовать для реализации любого определенного события в виде дерева. Только на выходной модуль, являющийся корнем дерева, подается входной

сигналена входной зажима. Входной сигнал задерживается схемой задержки D и подается на четыре модуля следующего уровня дерева. Другие типы рассмотренных ранее модулей также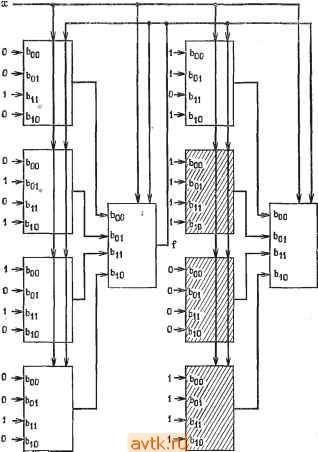

Рис. 6.18 Модульная реализация с одним контуром обратной связи, пример 6.6.

могут быть преобразованы подобным же образом для ограничения коэффициента разветвления по выходу.

Рассмотренные в этом разделе виды реализации могут быть полезны в связи с развитием большой степени интеграции, поскольку способ соединения не зависит от вида реализуемого автомата. Таким образом, в принципе возможно конструирова-

00-

D-0 D-[>

10---

Рис, 619. Модуль для древовидной реализ.ацин с фиксированным коэффициентом разветвления по выходу.

к некоторым входным зажимам, обеспечения достаточного количества уровней деревьев и необходимого числа входов модулей.

6.3. КЛЕТОЧНЫЕ СТРУКТУРЫ

Клеточные структуры являются еще одним классом цепей, предлагаемым в качестве средства для реализации преимуществ высокой плотности логических элементов, появление которой связано с развитием большой степени интеграции. В этом разделе мы рассмотрим цепи, составленные из однотипных элементов, соединяемых в виде одно- или двумерных массивов. Каждый элемент при такой структуре имеет фиксированное число входов и выходов. Будем рассматривать два различных типа структур: первый, в котором все элементы реализуют одну и ту же функцию, и второй, в котором функции, реализуемые различными элементами, могут различаться. Структуры, в которых элементы идентичны, называются итеративными. Клеточные структуры удобно классифицировать как односторонние структуры, в которых перемещение сигнала идет в одном направлении каждого из измерений, и двусторонние структуры, в которых сигналы распространяются в обоих направлениях каждого из измерений. Иначе говоря, при односторонней одномерной

ние универсальных последовательностных цепей, которые могут быть использованы для реализации любого последовательностного автомата путем подачи соответствующих констант

Х2 SCs х„

1 Ж J-

Рис. 6.20. Одномерная структура.

выводу в цепи, то такая структура называется неизбыточным каскадом Мэйтра. Поскольку число различных функций, реализуемых этим каскадом из (п-1) элементов, является п! X Х(16 ~), а число комбинационных функций п переменных равно 2 , то очевидно, что для > 4 все комбинационные функции п переменных не могут быть реализованы при использовании неизбыточного каскада Мэйтра. Можно показать [31], что даже избыточные каскады Мэйтра, в которых одна и та же входная переменная может быть соединена более чем с одним элементом, не могут реализовать все комбинационные функции. Увеличение числа соединений между элементами также недостаточно для логической завершенности линейного каскада таких элементов.

Одним из типов линейных каскадов, завершенных логически, является каскад элементов с парафазным входом и двумя соединениями между элементами [29]. Предполагается, что каждый элемент может реализовать любую пару комбинационных функций трех переменных. Чтобы продемонстрировать возможность реализации комбинационной функции таким каскадом с двойными связями, рассмотрим элементы с тремя входными и двумя выходными сигналами, причем входными сигналами являются сигналы X, Ух, уг, а выходными сигналами ух и у2. Пусть =

клеточной структуре сигнал распространяется слева направо (или справа налево, но никогда в обоих направлениях одновременно), в то время как при двусторонней структуре сигналы могут распространяться в обоих направлениях.

6.3.1. ОДНОМЕРНЫЕ КЛЕТОЧНЫЕ СТРУКТУРЫ

Простейший тип клеточной структуры состоит из линейного каскада элементов комбинационных логических схем с двумя входами и одним выходом, как показано на рис. 6.20. Мэйтра [16] изучил проблему реализации произвольных комбинационных функций с помощью цепей подобного рода, при этом предполагалось, что каждый элемент может реализовать любую из 16 комбинационных функций двух переменных. Если каждая входная переменная подсоединяется к одному определенному

Рис 6.21. Реализация функции на каскаде с двойными входами, пример

Можно показать [29], что каскад с двойными входами может использоваться для реализации произвольной пары комбинационных функций. Каскад с двойными входами обобщается также на случай каскада с множественными входами для реализации произвольных множеств функций [4]. Каскад с г входами является линейным массивом элементов комбинационных логических схем с 1) входными и г выходными сигналами. Выходные сигналы элементов соединяются со всеми входами следующего элемента. Каждый элемент обладает единственной (либо X, либо х) входной переменной, как и в случае каскада с двойными входами. Дальнейшее обобщение может быть связано с разрешением ввода в каждый элемент более чем одной входной переменной.

= fi(x, Уи У2), а p2 = gi{x, у и У2), 1= 1,2,3, где и gi определяются следующим образом:

и=ху1 !2ХУи 3=1,

giy-i-xyx, g2==y2 + xyu g3 = y2-

Обозначим элемент, реализующий функции yi = fi{x, уи У2) и y2 = gj{x, у\, У2), через {fi, gj). С помощью этих элементов девяти типов можно реализовать любую комбинационную функцию в виде суммы произведений путем формирования произведений на г/ь идущих от элементов {fu gs) или (/г, ё'з). и суммирования их на у2, идущих от элементов (/з, gi) или (/3, g2). Верхней границей числа элементов, необходимых для реализации функций п переменных, является величина п-2 . Минником и др. [19] разработано несколько методов получения более экономичных каскадов с двойными связями.

Пример 6.7. На рис. 6.21 показан способ реализации функции .1-<2- з +- i;i- 23 на каскаде с двойными входами.

6.3.2. ДВУМЕРНЫЕ КЛЕТОЧНЫЕ СТРУКТУРЫ

Двумерные структуры представляют интерес, поскольку с их помощью могут быть реализованы произвольные комбинационные и последовательностные цепи из относительно простых элементов. Для использования в двумерных клеточных структурах предполагается несколько различных типов элементов, таких, как НЕ-И, НЕ-ИЛИ, и большинство логических элементарных схем. Рассмотрим сперва двумерные итеративные структуры элементов одноразрядного сумматора (полусумматора), которые реализуют сумму х=х@у на горизонтальном выходе и перенос - ху на вертикальном выходе, как показано на рис. 6.22, а.

1 I

г ! L i

т

Рис. 6.22. Матрица на элементах одноразрядного сумматора.

Структура таких элементов, реализующая комбинационную функцию п входных переменных, показана на рис. 6.22, б.

Рассмотрим двумерную структуру элементов, состоящую из п строк и 2 столбцов, в которой входные сигналы Хи Хъ Хп подаются на левую границу, а на все элементы верхней строки подается константа 1. Нетрудно убедиться, что выходные сигналы у элементов п-й строки соответствуют 2 минтермам п переменных. Для реализации произвольной комбинационной функции добавим снизу матрицы, реализующей данную структуру'), строку-коллектор, у которой на вход х подается нулевой сигнал, как показано на рис. 6.22, б. Для реализации функции / вертикальные выходы элемента в п-строке соединяются со строкой-

) В дальнейшем, поскольку объединение элементов в такой структуре образует матрицу, будем именовать ее просто матрицей. -- Прим. ред.