Нижние границы числа выводов, требуемых в УЛМ и-го порядка с соединениями между выводами, могут быть получены путем определения нижних границ числа блоков при разбиении и числа необходимых вспомогательных функций. Доказательство этого [25] довольно сложно и опускается.

На рис. 6.5 указаны нижние границы и конструктивные верхние границы числа выводов в УЛМ п-го порядка для четырех рассмотренных выше типов УЛМ [25, 30].

6.2. МОДУЛЬНАЯ РЕАЛИЗАЦИЯ

ПОСЛЕДОВАТЕЛЬНОСТНЫХ АВТОМАТОВ

В гл. 5 мы рассматривали задачу декомпозиции последовательностных автоматов на последовательные и параллельные соединения более простых автоматов. В этом разделе рассматривается более общая задача декомпозиции и требования к типизации модулей. Ограничим наше рассмотрение декомпозицией синхронных автоматов Мура на модули, которые также являются синхронными автоматами. Способ функционирования синхронных последовательностных модулей удобно представлять введением в них типовых задержек.

Пусть Т = {t\, /2, .. , /д} - множество типов модулей, и предположим, что каждый тип может представляться любым числом модулей. Пусть является логической сетью, составленной путем соединения входов каждого модуля с внешними входными и выходными сигналами других модулей или логическими константами О или 1. Пусть N имеет такое же число выводов для входных и выходных сигналов, что и последовательностный автомат М. Говорят, что сеть N реализует автомат М, если внешне поведение логической сети неотличимо от поведения автомата М.

Сеть N реализует автомат М с задержкой k, если выходная последовательность, полученная в сети N в ответ на любую входную последовательность, такая же, как в М, и она задержана на k единиц. Арден [2] показал, что множество типов модулей может реализовать любой последовательностный автомат при наличии задержки, если оно может реализовать определенное событие при отсутствии задержки.

6.2.1. ПОСЛЕДОВАТЕЛЬНОСТНЫЕ АВТОМАТЫ С ФИКСИРОВАННЫМ ЧИСЛОМ ВХОДОВ

Если ограничить класс последовательностных автоматов, который требуется реализовать таким образом, чтобы число входных символов было фиксировано, скажем tii (или меньше), то возможна реализация с нулевой задержкой любого представителя

Рис. 6.6. Модуль для реализации последовательностного автомата.

модуля nii соединяются с выходом некоторого модуля (возможно, самого nii) или с константой О или 1. При таком соединении выходной сигнал любого модуля в момент времени (/-+-1) является функцией входного сигнала х и сигналов на &о и &i в момент времени t. Если выходные сигналы модулей сети представляют переменные состояний, то такая сеть может реализовать любой последовательностный автомат, при этом обеспечивается использование правильного кодирования состояний.

Рассмотрим модуль mi, который задает двоичный выходной сигнал Z автомата М. Если выход этого модуля представляет переменную состояний уи то г/i должна быть равна 1 для тех состояний, которые имеют на выходе единицу и равна О для тех состояний М, которые имеют на выходе нуль. Если входы &о и bi подсоединены к выходам модулей niz и Шз, определяющим соответственно переменные состояний г/2 и г/з, то г/2 должна равняться 1 для всех состояний, элемент следующего состояния которого в нулевом столбце является состоянием, для которого г/1 = 1, а г/з должна равняться 1 для всех состояний, элемент

ЭТОГО класса путем соединения модулей только одного типа. Можно показать [10], что любой модуль, используемый для реализации автомата на k входов, должен иметь по крайней мере один выход, два состояния v\ k-\-2k входов. На рис. 6.6 показан модуль на 3 входа, который можно использовать для реализации модели любого последовательностного автомата Мура с одним двоичным входом [32, 33, 35]. Выходной сигнал модуля в момент (4-1) как функция других сигналов в момент t задается в виде

Y = abi-\- abo.

Рассмотрим сеть N, полученную путем соединения модулей типа, показанного на рис. 6.6: вход а каждого модуля соединяется с внешним двоичным входом х. Входы bo и &i каждого

следующего состояния которого в единичном столбце является состоянием, для которого у] = 1. Входы Шг и Шз могут быть определены подобным же образом и процедура может быть продолжена до тех пор, пока не исчезнет потребность в каких-либо дополнительных модулях.

Для получения формальной процедуры декомпозиции автомата М определим понятие /j-предшественник состояния Qi (обозначим его через N-{qi, Ij)) как множество состояний, для которых элементом следующего состояния в столбце Ij автомата М является Qi. Иначе

N-iQi, li){qk\N{qk, /у) = Л-

Аналогично /3-предшественник множества состояний Qi является множеством состояний, для которых элементы следующих состояний в столбце Ij являются элементами

N-{Qi, Ij)={Qk\N{Qk, )eQJ.

Для автомата Мура М с одним двоичным входным сигналом х и одним двоичным выходом Z следующая процедура может использоваться для модульной реализации сети автомата М с помощью модулей, изображенных на рис. 6.6. Процедура 6.1

1) Строим направленный граф, вершинами которого являются подмножества состояний М, а ребра соответствуют входным символам следующим образом:

а) начальной вершиной назовем вершину, которая соответствует состояниям М, создающим на выходе единицу');

б) определяем вершину, соответствующую множеству 0-пред-шественников первой вершины, и соединяем ребром, помеченным цифрой О, вновь добавленную вершину с первой вершиной. Аналогичным образом определяем вершину, соответствующую 1-предшественникам первой вершины и соединяем ее с первой вершиной ребром, помеченным цифрой 1;

в) для каждой уже существующей вершины графа добавляем вершины, соответствующие их предшественникам, как в п. б). Если вершины, соответствующие каким-либо предшественникам, уже есть на графе, то добавляются ребра, выходящие из имеющихся вершин. Построение графа заканчивается, когда на графе содержатся вершины предшественников каждой вершины и соответствующие ребра. Если автомат имеет п состояний, то граф будет содержать максимум 2 вершин.

2) Модульная реализация автомата М получается из графа путем замены каждой вершины графа модулем типа изображен-

) Код вершины строится как перечень соответствующих состояний. - Прим. перев.

НОГО на рис. 6.6. Ребро, помеченное цифрой О, заменяется соединением с выводом &о модуля, соответствующего вершине, в которое ребро направлено. Аналогично ребро, помеченное цифрой 1, заменяется соединением с выводом Ь\. Внешний входной сигнал X соединяется с выводами а всех модулей. Вершина, со-

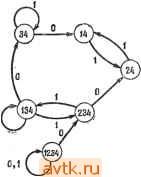г

Рис. 6.7 Таблица состояний (а); граф (б); модульная реализация (в) (пример 6.2).

ответствующая множеству всех состояний (если она есть на графе), заменяется константой 1, а пустое множество - константой 0. Таким образом, верхней границей числа модулей, требуемых для реализации автомата с п состояниями при использовании этой процедуры, является величина 2 - 2.

Пример 6.2. Для таблицы состояний, показанной на рис. 6.7, с, первый шаг процедуры 6.1 приводит к графу, изображенному на рис. 6.7,6, который далее преобразуется в модульную реализацию, показанную на рис. 6.7, е. Выводы а всех модулей соеди-

Рис 6.8. Еще один тип модуля для реализации последовательностного автомата.

модулей, изображенных на рис. 6.6, дает также возможность получить модульную реализацию модели последовательностного автомата Мили с одним входным сигналом. В этом случае автомат М реализуется с задержкой 1, хотя элемент задержки может быть вынесен из выходного модуля. Выходная вершина графа может быть помечена буквой z (так как она не используется как часть кодирования состояний), вход &о соединяется с вершиной, соответствующей множеству всех состояний М, которые создают выходной сигнал z = 1 при нулевом входном сигнале, а вход &1 соединяется с вершиной, соответствующей множеству состояний автомата М, которые создают выходной сигнал Z = 1 при единичном входном сигнале. Остальная часть графа строится и преобразуется в модульную реализацию так же, как в случае автомата Мура (процедура 6.1).

Другой тип модуля [10], который может использоваться для реализации любого двоичного последовательностного автомата, показан на рис. 6.8. Так же как и в реализации с использованием модуля, показанного на рис. 6.6, вывод а каждого модуля соединяется с входом последовательностного автомата. Выводы

нятся с входным сигналом х, но эти соединения на рис. 6.7, в опущены, чтобы не перегружать рисунок. Отмечая выходы модулей как переменные состояний, как показано на рис. 6.7, в, получаем следующую таблицу кодирования состояний, соответствующую модульной реализации:

г/1 У2 Уз yi Уъ 10 110 0

2 0 0 0 1 1

3 110 10

4 111 11

Если последовательностный автомат, который необходимо реализовать, имеет более одного выходного сигнала, то шаг 1а процедуры 6.1 повторяется для каждого выхода. Использование

а

ь

6о И bi соединяются с выводами для выходных сигналов других модулей или с константами О или 1 Для этого модуля если л: = О, то Y = Ьо- Таким образом, &о представляет собой множество 0-предшественников у. Если х-1, то У = &о©&1- Следовательно, Ь] представляет собой объединение множеств 0-предшественников, не являющихся и 1-предшественниками, и 1-пред-шественников, не являющихся и 0-предшественниками.

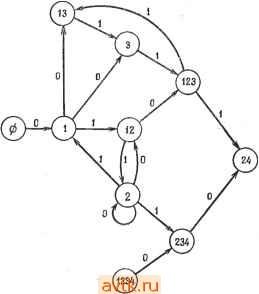Рис. 6 9 Таблица состояний (а); граф (б) (пример 6.3).

Для использования модулей этого типа процедура 6.1 может быть модифицирована следующим образом. Начиная от вершины, соответствующей состояниям, которые создают на выходе единицу, строим граф, как и прежде, за исключением того, что вершина, соответствующая 1-предшественнику, заменяется вершиной, помечаемой как объединение 1-предшественников, которые не являются также и 0-предшественниками, и 0-предшественников, не являющихся и 1-предществергаиками.

Пример 6.3. Реализация последовательностного автомата примера 6.2 с использованием модуля, изображенного на рис. 6.8, показана на рис. 6.9. Модульная реализация может быть получена непосредственно из графа, изображенного на рис. 6.9, б, как в примере 6.2.

Рис. 6.10. Модуль для реализации последовательностного автомата с несколькими входными сигналами.

Вместо определения О- и 1-предшественников подмножеств состояний автомата определяем /j-предшественник, О / 2=- 1, где Ij представляет собой входной столбец таблицы состояний

bi2-

Рис. 6.11. Модуль для реализации последовательностного автомата с 2г-J- 1

входами.

автомата М. Построение графа и модульная реализация выполняются таким образом, как рассмотрено ранее.

Поскольку модуль, показанный на рис. 6.6, годится для реализации любого автомата Мура с двоичным входом, то число модулей, требуемых для модульной реализации, может быть уменьшено ценой увеличения сложности модуля. На рис. 6. И

Модуль, показанный на рис. 6.6, может быть модифицирован (рис. 6.10) для реализации последовательностных автоматов с более чем одним двоичным входным сигналом [35]. Процедуру 6.1 можно изменить для реализации любого автомата Мура М с k или менее двоичными входными сигналами при использовании модулей только такого типа, какой изображен на рис. 6.10.

показан модуль с 2г входами в модуль аналогично двум входам Ьо и Ъ\, показанным на рис. 6.6 и 6.8. Этот модуль также можно изменить, как показано на рис. 6.10, для реализации автоматов с k или менее двоичными входными сигналами.

При использовании модуля, изображенного на рис. 6.П, для реализации любого последовательностного автомата с одним входным и одним выходным сигналами выходы а каждого модуля должны быть соединены с входами автомата, как в рассмотренном ранее случае, с модулем на 3 входа. Выходной сигнал модуля будет равен 1 тогда и только тогда, когда х = О и boi = 1 или X = 1 и = 1, 1 г г Таким образом, если каждый модуль в реализации относится к множеству состояний Qo, для которых их выходные сигналы должны быть равны 1, как в процедуре 6.1, то объединение этих модулей, соединенных с выходами Ьог, будет 0-предшественниками состояний Qo, а объединение этих модулей, соединенных с выходами Ъм, будет 1-предшественниками состояний Qo-

При использовании модуля, изображегшого на рис. 6.11, процедуру 6.1 можно модифицировать следующим образом. Пусть Q является множеством всех состояний автомата. Разделим Q на г блоков Qi, Q2, .... Qr, имеющих максимум \п\г\ состояний в блоке, где п - общее количество состояний автомата. Выходной модуль соответствует множеству состояний, которые должны иметь на выходе единицу. Определяются О- и 1-предшественники и находятся их пересечения с Qi, Q2, ..., Qr для определения тех модулей, которые должны соединяться с выходами Ьог и Ъ\г соответственно. Процедура повторяется для каждого уже имеющегося в цепи модуля до тех пор, пока не исчезнет необходимость в каких-либо новых подмножествах состояний. Поскольку существует (21 /-1) непустых подмножеств с \Ыг\ или менее состояниями, верхней границей числа модулей при такой реализации является 1 --г(21 2 - 1). Отметим, что эти границы не зависят от числа двоичных входных сигналов последовательностного автомата. Реализация, удовлетворяющая таким же границам, может быть получена при использовании для реализации последовательностных автоматов с k входами модулей zk-\- входными сигналами [33].

Пример 6.4. Рассмотрим таблицу состояний (рис. 6.12, а), которую необходимо реализовать, используя модули на 5 входов (т.е. /- = 2). Пусть произвольным разбиением множества состояний будет (123, 456). Поскольку состояния 3, 4 и 6 определяют выход 2=1, отмечаем выходной модуль номером 346. 0-и 1-предшественниками этого множества являются соответственно {156} и {2456}. Их пересечения с {123} и {456} дают {1}, {56}, {2}, {456}. Определяя О- и 1-предшественников этих состояний и находя их пересечения с двумя блоками разбиения, получаем

2 3 4 5 6

3 5 2 1

2 4 1 6 3 3

О

о 1 1

01 biz

Ьог biz

Ь02 . Ь,2

bo, Ь02 Ьц Ь,2

Ь01 Ьц

-Jb)2

[ I Рис. 6.12. Таблица состояний (а); модульная реализация (б) (пример 6.4).

Процедура завершается, поскольку предшественником состояния 5 является состояние 2, которое уже было рассмотрено. Таким образом, модульная реализация требует 8 модулей, как показано на рис. 6.12,6.

дополнительные подмножества {4}, {3} и {6}. Повторение процедуры приводит к добавлению единственного подмножества {5}.

В ТО время как процедура 6.1 приводит к единственной модульной реализации из модулей на три входа, этот факт не имеет места в случае модулей с (2г+1) входами, где г>1.

ь01 Ь,2

ь01 Ь.1

Ь|г

ь01 Ь,2

Рис. 6.13. Модульная реализация при разбиении (135, 246) (пример 6.5).

Если бы мы выбрали разбиение (135, 246), то получили бы реализацию, показанную на рис. 6.13 при той же таблице состояний.

6.2.2. ДРЕВОВИДНЫЕ СТРУКТУРЫ

Другим желательным свойством модульных реализаций является типизация структуры внутренних соединений. Описанную в предыдущем разделе процедуру можно модифицировать та-