ЭТОЙ функции Б виде произведений сумм можно получить, используя минимальную реализацию в виде суммы произведений функции f.

Пусть f = Ц Pi, где / - множество простых импликант

в минимальном покрытии f. Тогда, используя, законы Де Моргана, получим

f= П л.

Так как каждый терм представляет собой произведение литералов, то на основании законов де Моргана Р,- будет суммой дополнений литералов Pi. Следовательно, минимальная

Рис 1.20. Выбор простых импликант с помощью карты Карнау.

Рис 1.21 Карта /.

реализация вида И-ИЛИ функции / получается непосредственно из минимальной реализации того же вида функции f путем дополнения всех входов и замены логических элементов И на ИЛИ, а логических элементов ИЛИ на И.

Процедура 1.3 Минимальное произведение сумм

1. Используя процедуру 1.1, находим минимальную сумму произведений функции f, т. е. / = Y, Pi (точки 1 и О функции

/ становятся соответственно точками О и 1 функции f; неопределенные точки функции / остаются неопредленными и для функции f).

2. Получаем реализацию функции в виде минимального произведения сумм путем дополнения всех входных переменных и замены логических элементов И на ИЛИ, а ИЛИ на И.

Пример 1.7. На рис. 1.21 показана функция f, для которой функция / задана картой Карнау, изображенной на рис. 1.20. Для функции f импликанта х^ представляет собой суще-

ственно простую импликанту для 1-точки 0101. После выбора этой импликанты и замены покрытых ей 1-точек на неопределенные приходим к импликанте XiXzXt, являющейся хорошей простой импликантой для 1-точки 1001. Импликанта xzXsXi - хорошая простая импликанта для 1-точки 1010, 3X1X3X4 - для 1-точки ОНО. Это простые импликанты покрывают все 1-точки функции f и образуют следующую минимальную сумму произведений: f = Х2Х3Х4 -f- X1X2X4 -j- Х2Х3Х4 -f- X1X3X4. Отсюда следует, что минимальная реализация функции / в виде произведения сумм равна f == (х2 + Хз -f Х4) (Xi -f Х2 -f Х4) (Х2 -f Хз -f Х4) (Xi + X3 -f X4) И

требует 16 логических входов. Минимальная реализация функции f Б виде суммы произведений, полученная в примере 1.6, имеет вид Х3Х4 -j- Х1Х2Х4 -\- ххх^хз и требует 11 логических входов.

Из примера 1.7 следует, что для получения двухступенчатой реализации минимальной стоимости нужно рассматривать реализацию как в виде суммы произведений, так и в виде произведения сумм.

Минимальная двухступенчатая реализация функции в виде НЕ-И может быть получена из ее минимальной реализации в виде суммы произведений следующим образом. Пусть f = ~ Р\ + Р2+ +Ph. Тогда, пользуясь законом Де Моргана, получим f= Р\-Р2- ... -Ph- Последнее выражение представляет собой выход элемента НЕ-И, входами которого являются Р\, р2, ... Ph- В СБОЮ очередь каждый вход Pi может быть образован с помощью элемента НЕ-И, входами которого являются литералы простой импликанты Pj. Следовательно, двухступенчатая реализация вида НЕ-И получается заменой всех логических элементов в двухступенчатой реализации вида И-ИЛИ элементами НЕ-И.

Аналогичная процедура используется для получения минимальной двухступенчатой реализации вида НЕ-ИЛИ из минимальной реализации в виде произведения сумм. Пусть f =

= Si-S2 ... 5ft. Тогда функция f = Si-\-82+ ... -j-Su реализуется заменой всех логических элементов в реализации вида ИЛИ-И на логические элементы НЕ-ИЛИ.

Существующая технология позволяет получить схемный эквивалент операции И или ИЛИ простым соединением определенных проводов. Например, в логике ТТЛ логический элемент И образуется соединением выходов (коллекторов) логических элементов НЕ-И. Аналогично для получения логических элементов ИЛИ нужно соединить выходы логических элементов НЕ-ИЛИ. Эти реализации можно получить непосредственно с помощью двухступенчатых элементов И-ИЛИ и ИЛИ-И. Например, реализация вида НЕ-И-И функции f получается путем замены логических элементов И в двухступенчатой реализации

И-ИЛИ функции f элементами НЕ-И и выходного элемента ИЛИ на И. Аналогичным образом, реализация вида НЕ-ИЛИ-ИЛИ функции f получается заменой логических элементов ИЛИ в двухступенчатой реализации вида ИЛИ-И функции f логическими элементами НЕ-ИЛИ и выходного логического элемента И на ИЛИ.

Рис. 1.22. Модульный я-разрядный сумматор.

Многие практически используемые комбинационные цепи реализуются в виде многоступенчатых цепей не с помощью таблиц истинности, а непосредственно на основе их функционального описания. Примерами такого подхода являются цепи, кото-

Рис. 1.23. Таблица истинности модульного сумматора.

рые выполняют операции на множестве связанных входов, составляющих слово . К ним, в частности, относятся схемы для сложения или сравнения двух чисел, выполняющие одинаковые операции на каждом разряде и передающие информацию в следующий разряд. Такие схемы могут быть реализованы в виде Каскадного соединения относительно простых идентичных модулей. Модульная конструкция часто требует значительно меньще оборудования, чем двухступенчатая реализация, и легко модифицируется при изменении числа обрабатываемых разрядов.

Однако разработка отдельных модулей может осуществляться с помощью таблиц истинности. Модульная конструкция -разрядного сумматора показана на рис. 1.22. Модули М, идентичны. Каждый из них имеет по три входа л; г/г, с, и два выхода и Ci J. 1. Входы Хг и Уг представляют собой складываемые числа, вход Ci - перенос из (t - 1) -го модуля в t-й, выход z, - результат сложения, а выход Ci + i - перенос. Каждый модуль характеризуется таблицей истинности, представленной на рис. 1.23. Минимальная реализация в виде суммы произведений имеет вид

Zl = XiyiCi + XiyiCi -f XiyiCi -f XiyiCi, Ci+l-=-Xiyi + XiCi + У1С1.

Из сказанного следует, что для реализации цепи достаточно иметь только таблицу истинности, описывающую основной модуль.

1.4. ПОСЛЕДОВАТЕЛЬНОСТНЫЕ ЦЕПИ

Функция, значение которой зависит не только от текущих, но и предыдущих значений входных переменных, называется по-следовательностной функцией, а ее реализация - последователь-постной цепью. Так как эта зависимость проявляется во времени, то представление последовательностных функций таблицами истинности, используемыми для комбинационных функций, является неадекватным.

1.4.1. ПОСЛЕДОВАТЕЛЬНОСТНЫЕ АВТОМАТЫ

Одним из методов описания последовательностей функции является построение математической модели, называемой по-следовательностным автоматом. На вход такого автомата поступают символы из конечного множества, называемого входным алфавитом /. На его выходе формируются символы, которые являются элементами конечного множества, называемого выходным алфавитом О. Последовательностный автомат имеет несколько внутренних состояний, ниже называемых состояниями. Входы, выходы и состояния автомата относятся к дискретным моментам времени. Ниже мы ограничимся изучением конечных автоматов, т. е. последовательностных автоматов с конечным числом состояний.

Обозначим через Q множество состояний автомата. Тогда его работа описывается следующим образом. Пусть некоторое начальное состояние автомата равно qi s Q. При поступлении на его вход символа /, е / он вырабатывает выходной символ ZkO и в следующий момент времени переходит в состояние

Пример таблицы состояний приведен на j 24. Таблица со-

рис. 1.24. Автомат имеет 4 состояния Q, стояний,

обозначаемые следующим образом: Q =

= {1,2,3,4}, и двоичные вход и выход / = О = {О, 1}. Входной символ в последовательностной цепи представляется комбинацией значений множества бинарных переменных {xJ.

Другим способом представления последовательностного автомата является диаграмма состояний {граф перехода состояний), в которой узлы характеризуют состояния, а ветви, обозначенные индексами Ij/z, - переходы с соответствующими входами Ij и выходами Zk. Диаграмма состояний, соответствующая таблице состояний на рис. 1.24, приведена на рис. 1.25.

Таблица или диаграмма состояний последовательностного автомата могут быть использованы для определения выходной последовательности, возбуждаемой любой входной последовательностью для любого начального состояния. Если для автомата, представленного таблицей состояний на рис. 1.24 или диаграммой состояний на рис. 1.25, начальное состояние равно 1, а входная последовательность Х = 00101, то он пройдет через последовательность состояний 22434 и сформирует на выходе последовательность 11010. Та же входная последовательность, приложенная при начальном состоянии 3, приводит к выходной последовательности 01010.

) Математически автомат Мили часто представляется вектором (/, О, Q, V, Z), где / - входной алфавит, О - выходной алфавит, Q - множество состояний, - отображение из / X О в Q, Z - отображение из / X Q в 2. Однако мы будем использовать представление в виде таблицы состояний, так как STO более удобно для проектирования последовательностных цепей.

q. е Q. Это новое состояние Qj и выходной символ однозначно определяются входным символом и текущим состоянием автомата.

Конечный автомат может быть представлен таблицей состояний, строки которой характеризуют все его состояния, а столбцы- все входные символы (иногда называемые входными состояниями). Элемент, записанный в строке столбца Ij, характеризует следующее состояние и выходной символ, получаемые в том случае, если Ij прикладывается в момент, когда автомат находится в состоянии qi. Эти величины на- х

зываются соответственно функциями перехода и функциями выходного символа и обозначаются соответственно N[qi, Ij), Z{qu Ij). Рассматриваемый тип последо-вательностного автомата, состояние выхода которого является функцией входного и текущего состояний, называется автоматом Мили) [13].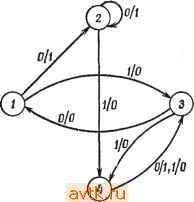

Рис. 1.25. Диаграмма состояний

Мура М', эквивалентный М в том смысле, что для любой заданной входной последовательности и соответствующих начальных состояний оба они генерируют одинаковые выходные последовательности [2]. Аналогично для каждого автомата Мура существует эквивалентный автомат Мили.

Автомат Мили, эквивалентный заданному автомату Мура, может быть получен с помощью следующей процедуры.

Процедура 1.4

1. Входной алфавит, выходной алфавит и множество состояний автомата Мили те же, что и для автомата Мура.

2. Пусть N, Z и N, Z - соответственно функции следующего состояния и выходного символа автоматов Мили и Мура. Тогда элементы таблицы состояний автомата Мили определяются следующим образом: если Л^((?г. lj)=9h, а Z{qh)-=Zh, то N(ди Ij) == qh, а Z{qi, Ij) = z.

) Автомат Мура может быть представлен вектором (/, О, Q, N, Z). В отличие от автомата Мили здесь Z есть отображение Q в О.

В рассмотренной модели последовательностных автоматов (автомат Мили) выход является функцией входа и текущего состояния, и, как показано на рис. 1.25, связан с переходом состояний. Другая модель последовательностных автоматов, называемая автоматом Мура [14], связывает выход не с переходами состояний, а с самими состояниями). Таблица состояний автомата Мура приведена на рис. 1.26. Предполагается, что входы и выходы обеих моделей относятся к дискретным моментам времени. Для любого автомата Мили М существует автомат

Таблица состояний автомата Мили, эквивалентного автомату Мура (рис. 1.26), полученная с помощью процедуры 1.4, приведена на рис. 1.27.

Следует указать на одно отличие между работой автоматов Мура и Мили. Если на вход автомата Мура (рис. 1.26) подать символ л; = 1 Б состоянии 1, то при / = 1 он перейдет в состояние 2 и сформирует выходной символ z=\. Если же л; = 1 подать на вход автомата Мили (рис. 1.27), находящийся в том же состоянии 1, то выход станет равным 1 при f = О, и при < = 1 автомат перейдет в состояние 2.

Рис. 1.26 Таблица состояний автомата Мура.

Рис. 1.27. Таблица состояний автомата Мили.

Автомат Мура М', эквивалентный данному автомату Мили М, должен обладать большим числом состояний, чем соответствующий автомат Мили. Для его получения используется следующая процедура.

Процедура 1.5

1. Входной / и выходной о алфавиты автомата М' те же, что и автомата М.

2. Если Q - множество состояний автомата М, а и Z - соответственно функции его следующего состояния и выходного символа, то множество Q автомата М' определим следующим образом: пусть Qi {qkm\N{qi, Ij) = Qk, Z(qiIj) = Zm для некоторого qiQ и некоторого /je/}. Пусть также Q2 = {qh\N{qi, h) Qk для всех (?г e Q и всех Ij e /}, т. е. Q2 - множество состояний из Q, которые не являются следующими состояниями М. Q = Q, и Q2.

3. Определим функцию следующего состояния Л^ автомата М' следующим образом: если N{qi, Ij) = qn и z{qu /,) = z, то Niqin, Ij) = Якт для всех qin е Qi и N{qi, Ij) = qum Для qiQz.

4. Определим функцию выходного символа Z автомата М' следующим образом: для qumQi Z{qkm) = Zm- Для (?i е Q2 Ziqi) не определена.

В таблице состояний автомата Мили, приведенной на рис. 1.24, существуют переходы в состояние 3 с выходными,

Рис. 1 28. Автомат Мура, эквивалентный автомату Мили, изображенному на рис. 1.24.

Рис. 1.29. Автомат Мили с запрещенной входной последовательностью

Как И в случае комбинационных функций, таблица состояний последовательностной функции может содержать неопределенные (безразличные) состояния. Эти состояния характеризуют условия, при которых для данного перехода из состояния <7,-(вход Ik) не нужно определять следующее состояние и/или выход. Такие условия существуют, если при нахождении автомата в состоянии <7г ВХОД Ih запрещен или если при разрешенном в состоянии Qi входе Ih следующее состояние и/или выход по каким-либо причинам нерелевантны. В качестве примера на рис. 1.29 приведена таблица состояний автомата Мили с запрещенной входной последовательностью /3/2. Если разрешены только начальные состояния 1, 4 и 5, то неопределенные переходы имеют место только при входных последовательностях, включающих в себя запрещенные последовательности.

1.4.2. ЭЛЕМЕНТЫ ПАМЯТИ

Для реализации последовательностного автомата последовательностной цепью необходимы средства представления его внутренних состояний. В настоящем разделе мы рассмотрим

символами О И 1. В соответствии с этим в таблице состояний эквивалентного автомата Мура, полученной с помощью процедуры 1.5, имеются две строки, характеризующие состояние 3 (а именно Зо и 3i). Переход к каждому из оставшихся состояний в таблице, показанной на рис. 1.24, не связан с появлением различных выходных символов, поэтому в таблице на рис. 1.28 каждому из этих состояний соответствует одна строка.

Техника анализа и синтеза обоих типов последовательностных автоматов аналогична, поэтому ниже мы рассмотрим ее применительно к модели Мили.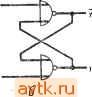

Рис. 1.30. PS-триггер. - представление; б - реализация; в - таблица состояний; г - таблица возбуждений.

волы (возбуждения) триггеров с их текущими и следующими состояниями. Из таблиц состояния видно, что выход у равен О в состоянии О и 1 в состоянии 1; у представляет собой дополнение у.

iS-триггер работает следующим образом: если вход 5 приводится в состояние 1 (5= 1), а вход R в состояние О, т. е. R = 0, то на выходе формируется символ 1 {у - I, у = 0); если 5 = 0, а R = I, то у = 0, у=1 (возврат в исходное положение), если S - R = О, то триггер устойчив в текущем состоянии. Входная комбинация S - R - \ является запрещенной, что отмечено в таблице состояния знаками неопределенности (-). В схемной реализации /S-триггера эта комбинация обеспечивает

различные типы элементов памяти, называемые триггерами или бистабильными элементами. Эти элементы обладают двумя устойчивыми состояниями, обозначаемыми как О и 1.

В последовательностных цепях широко используются триггеры, показанные на рис. 1.30-1.33. На этих же рисунках приведены таблицы состояний, описывающие поведение триггеров, и таблицы возбуждения, связывающие заданные входные сим-

в

Рис. 1.31. /К-триггер. а - лредставление; б - таблица состояний; в - таблица возбуждений.

Т

О I

Рис. 1.32. Г-триггер. а - представление; б - таблица состояний; в - таблица возбуждений.