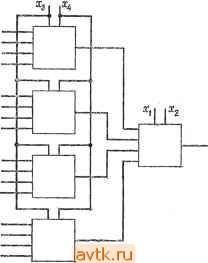Рис. 6.2. Реализация УЛМ пятого порядка с полгощью УЛМ третьего порядка.

казана реализация УЛМ пятого порядка, выполненная этим методом.

6.1.3. УЛМ с ПАРАФАЗНЫМИ ВХОДАМИ

В УЛМ с одинарными входами, рассмотренными выше, входы Zi, где п -f 1 г п -f- 2 , соединялись с логическими константами О или 1. Число требуемых выводов может быть уменьшено путем реализации УЛМ таким образом, чтобы любые Xj или Xj, где 1 / п, также могли быть соединены с любым

выводом Zi, П + I i П 2.

На рис. 6.3 показана каноническая реализация УЛМ для п переменных с парафазными входами, предложенная Препарата и Мюллером [28]. В такой реализации множество всех минтермов п переменных разделено на t блоков. Блок, обозначенный через Fi, реализует сумму минтермов, содержащуюся в блоке Рг. Общее требуемое число выводов для входных сигналов равно -f /.

Каждый блок Рг должен удовлетворять условию избирательности, которое определяется следующим образом: для каледого

13 Зак, 841

Каждая функция fab (л^з. . в свою очередь может быть раскрыта через и х^. Такой процесс повторяется до тех пор, пока не останется единственная переменная л; . На рис. 6.2 по-

z2-r

Рис. 6.3. УЛМ с парафазными входами.

Пример 6.1. Пусть Рг является множеством минтермов {XiXzXXi, XiXzXsXi, XiXzXXi}. Легко убедиться, что это множество удовлетворяет условию избирательности. Мы можем получить сумму любого подмножества минтермов из Pi путем умножения Fi на соответствующую переменную или константу следующим образом:

тогда

Fi = XiXXXi + XiXiXi + XiXXsXi,

XiFi - х^х^х^Хц,

x4f1 = XiXzXsXn,

XzFi = x1x2x3x4, XzFi = XiXXi -f XiXXi, XiFi = X1X2X3X4 XiXxXi, XiFi = .1.2X3X4 + XiXxXi, OFtO,

I Fi= XiXX-iX -\- XiXXsXi -f XiX~2XoXi.

Для разбиения на блоки множества всех минтермов удобна такая матричная запись, чтобы каждый блок Р^ удовлетворял условию избирательности. Пусть блок Рц содержит s минтермов

непустого собственного подмножества Pi существует переменная Xi, представленная во всех минтермах подмножества без ее дополнений, а во всех прочих элементах Pi с дополнениями или наоборот. Если блок Pi удовлетворяет условию избирательности, то сумма любого подмножества минтермов в Pi может быть реализована путем умножения (использования схем И) выходов Fj на некоторую переменную Xj или Xj или константу О или 1.

0 0 10 LO 1 1 I

примера 6.1 удовлетворяет этому условию. Рассмотрим теперь способ разбиения, при котором блоки удовлетворяют этому условию.

Пусть Л -матрица sXi. представляющая блок разбиения, и пусть i-я строка матрицы Л будет обозначена как а; = = {ciiu cii2, Clin), где ац=0 или 1. Каждая строка матрицы Л может рассматриваться как -мерный вектор, состоящий из нулей и единиц. Если vn - (Vhi, .. , г'йп) является любым другим п-мерным вектором, состоящим из нулей и единиц, то можно определить другую матрицу размера sX В = А, где i-я строка матрицы В определяется как Ь; = (Ьц, Ьй, bin), а bij = Vhj ф aij. Таким образом, если

и v, = (0110).

Если матрица Л удовлетворяет условию избирательности, то матрица В также удовлетворяет этому условию. (Это следует из того факта, что добавление к каждой строке матрицы Л просто выполняет операцию обращения тех столбцов матрицы Л, которые соответствуют единицам в v.) Если мы можем создать один блок, представленный матрицей Л, то другой блок может быть получен из равенства В = Л ф у^. Остальные блоки могут быть получены подобным же образом путем использования различных п-мерных векторов. Несмотря на то что все блоки, полученные этим методом, будут удовлетворять условию

п переменных. Мй представляем этот блок матрицей s Xв которой каждая строка соответствует минтерму. Элементом t-й строки и /-ГО столбца будет О или 1 в зависимости от того, представлена переменная Xj без дополнений или с дополнениями в i-M минтерме. Можно показать [26,30], что условие избирательности может быть удовлетворено блоком в том и только том случае, если его матрица такова, что для любого целого q, 1 9:2 - 2, некоторый столбец матрицы (или обратный код некоторого столбца) является двоичным кодом q. Матрица

п о о п

избирательности, они могут не оказаться непересекающимися. Так, если матрицы А и В будут определены, как ранее, и мы определим Б' = Л 0 Vm, где v = (10 00), то

ГО О О П

О

1 -i

обе матрицы и В и В' содержат вектор (1 1 1 1).

Для того чтобы использовать эту процедуру, порождающую непересекающиеся матрицы, удовлетворяющие условию избирательности, определим специальную начальную матрицу А*, которая удовлетворяет условию избирательности и к тому же задает векторы таким образом, что

v, ©a*=5v©aj для тф k.

Пусть число переменных п будет таким, что 2- - 1 п 2 -1, а s-e=2. Следующая процедура может быть использована для определения таких двух матриц Л* и V, что множество матриц УгфЛ* расчленяет множество 2 п-мерных векторов на 2 -непересекающихся подмножества, каждое из которых содержит 5 = 2 векторов. Пусть Is-i является тождественной матрицей размером (s-l)X(s-1), т.е. такая матрица, элементы i-й строки и /-го столбца которой равны 1, если i = /, и равны О в противном случае, и пусть t/s-i является матрицей размером (s - 1) X (2~-s), все столбцы которой отличны друг от друга и в которой столбец i содержит ki единиц, 2kis-l. Тогда Л* определяется как матрица s X , имеющая следующую структуру:

О

О

о

о

Последняя строка и правый (п -2*-1)-й столбец матрицы Л* являются нулевыми. Если п = 7 и 2 - - 17<:2* - 1, то S = 4 и г = 2.

1 О 0;0 1 1 1 1 oil О 1 1 ill 1 О 1

О О

о о

о;о о

о

в этом случае нет необходимости в нулевых столбцах. Однако если 7 15, то S = 4, а нулевой столбец должен быть добавлен к правой части матрицы. Если, например, п - 9, то матрица будет иметь два нулевых столбца.

1 0 1 0 0 0 0

а вектор v е V должен удовлетворять условиям © 0,3 = О и Vi\ ф гг - 0. что влечет за собой vn = Vi - Viz- Поскольку это должны быть нули или единицы и нет ограничений на оставшиеся компоненты м, то существуют 2 X = 2 векторов, удовлетворяющих ограничению. Такие векторы образуют разбиение на 32 блока по четыре минтерм а в блоке.

Если бы п = 9, то единственным отличием в результате было бы то, что матрицы Л* и G имели бы два добавочных нулевых столбца. Это привело бы к разбиению на 2 блоков по четыре минтерма в блоке.

Лемма 6.2. Если V; е F и v, е 1/, то Vj©Vj е V.

п

Доказательство. Если Vj е F, то Yj Vigkm = 0. где 1 :< г.

п

Подобным образом если VjV, то Imgkm - , ikr.

Следовательно, Y /mФ in) gkm = 0, 1 < fe < r, и Vj © Vy e F.

m = l

Лемма 6.1. Определенная ранее матрица А* удовлетворяет условию избирательности.

Доказательство. Предоставляется читателю в качестве упражнения.

Матрица Л* порождает один блок разбиения. Остальные блоки будут получаться с помощью задания векторов v, и их добавления к матрице Л* для создания Вг- = Л'фУг. Для доказательства того, что эти блоки являются непересекающимися, необходимо ограничить эти векторы таким образом, чтобы

Vi©aft=5v;©a.

Множество векторов V, которое удовлетворяет этому ограничению, определяется следующим образом: пусть Н - матрица rX(s-1)> причем столбец i матрицы является двоичным кодом i для 1 г^5- 1. Пусть G является матрицей гУп, полученной прибавлением нулевых п -s + 1 столбцов к Я. Иначе, G = [H\0]. Теперь V является матрицей, удовлетворяющей условию i/-G = [0] по арифметическому модулю 2, где G - транспонированная матрица G. Иначе, Vi = {viu и^, fin) является строкой V в том и только в том случае, если

п k = \

При S = 4 и г = 2

0 1 1 О О О ОТ

Теорема 6.1. Если А* и V таковы, что определено выше, и V/, V/sF, а Ей, а^еЛ*, то а^фу =5 aevy.

Доказательство. Предположим ф V; = ф v,-. Тогда айфа = Vj©V/е 1/ в соответствии с леммой 6.1. Поскольку aj.a являются строками матрицы Л*, k,ms. Если k, ms - 1, то (а^.фа; ) имеют 1 только в k-u и т-м столбцах среди первых S - 1 столбцов. Так как первые s- 1 столбцы матрицы G представляют различные числа, то должна существовать строка gf; матрицы G, содержащая 1 в столбце й и О в столбце т или наоборот. Тогда

Z (Щр Ф Vjp) gip = Е (c!ftp Ф а^р) gtp ф О р= р=1

и (Vj©v/)el/, если m = s, а^ = (0, О, ..., 0) иайфа^ = аА, Следовательно, у^фУу^У, что является противоречием.

Можно показать, что матрица V имеет 2 - строк. Из теоремы 6.1 следует, что матрицы I/ и Л* могут использоваться для разбиения множества 2 минтермов на 2 - непересекающихся блоков по 5 = 2 минтермов в блоке. Для случая п - 1 с использованием этого разбиения УЛМ может быть реализован на семь переменных с 39 выводами для входных сигналов. УЛМ Яу - Танга на семь переменных требует 2 + 6 = 70 выводов для входных сигналов.

Если 5 не является степенью двух, для получения желаемого разбиения приведенная процедура может быть модифицирована следующим образом. Пусть г -\\o2s\, где \х\ является наименьшим целым, большим или равным х. Процедура порождает разбиение, состоящее из 2 - блоков размером 2°\ Общее число минтермов, включаемых в блоки, равно 2 ° ° < 2 . Рассмотренная выше модификация процедуры может быть использована для определения меньших блоков и для покрытия оставшихся минтермов [28].

6.1.4. УЛМ С СОЕДИНЕНИЯМИ МЕЖДУ ВЫВОДАМИ

Число переменных, требуемых УЛМ п-порядка, может быть уменьшено еще в большей степени путем осуществления связей между некоторыми выводами в добавление к обеспечению пара-фазных входов. Следующий метод построения УЛМ шестого порядка может быть обобщен на УЛМ п-порядка [37].

Любая функция шести переменных может быть выражена как

fiXuXz, Xe)=X3XiX5X6foOOo{X\,X2)+ ... +X3XiX5X6fnn(.Xi, Х2).

Если В является УЛМ пятого порядка, то любая функция шести переменных может быть реализована путем соединения соответ-

ствующих функций двух переменных ХиХгС выводами Zu Zie (рис. 6.4). Если цепь, обозначенная через А, реализует десять нетривиальных функций двух переменных, то любая функция шести переменных может быть реализована путем соединения выводов Уг.....Ую или Xi, х\, лгг, Xz, О или 1 с выводами

1, .... ZlQ.

Этот метод может быть обобщен на реализацию УЛМ большего числа переменных. Например, УЛМ двенадцатого порядка может быть реализован с использованием трехвходовых подсхем

rCj ajj Xg

Hi Уг ho h Ч

Рис. 6.4. УЛМ шестого порядка с соединениями между выводами.

А И УЛМ В на 10 переменных. Цепь А будет иметь три входных и - (2 X 3 + 2) = 248 выходных сигналов. УЛМ В на 10 переменных будет иметь 28-f 9 = 521 вход. Общее число выводов в таком УЛМ, исключая выводы для выходных сигналов, будет 248 -f 3 -Ь 521 = 772 по сравнению с 2 -f 11 = 2059, требуемых для УЛМ десятого порядка с одним парафазным входом, рассмотренным ранее. УЛМ -порядка, использующий цепь А на г входов и УЛМ В с п - r-fl входным сигналом, потребует = г -f 2* -f 2 - - 2г -f - 1 вывода. Естественно, что для любого г может быть выбрано таким образом, чтобы минимизировать Л^.

Метод разбиения множества всех минтермов, используемый для канонической реализации УЛМ с парафазными входами, рассмотренный ранее, может быть модифицирован для случая /= {0,1,1, Хх, Xz, Xz, Хп, Хп, gl, gz, gs]- Условие избирательности разбиения будет зависеть от множества вспомогательных функций {gl, gz, gs]- УЛМ также реализует эти вспомогательные функции, так как любые функции п переменных могут быть реализованы путем их соединения со входами Zi, i > п.

Для выбора вспомогательных функций пока не существует каких-либо известных систематических методов использования

О

Используя условие избирательности, определенное ранее, мы видим, что г^ножество минтермов, представленных второй и третьей строками (а также множество, представленное первой и четвертой строками), не может быть выбрано без вспомогательных функций, поскольку не существует столбца с кодом 0 110 (или его обратным кодом). Все остальные подмножества минтермов могут быть выбраны. Однако желаемый столбец может быть создан путем сложения (по модулю 2) первых двух столбцов. Следовательно, если Xi @х2 и Xi@x2 доступны в качестве вспомогательных функций, то могут быть выбраны любые подмножества минтермов. Остальные блоки разбиения могут быть получены путем вычисления Л* ф v, v е У, где множество векторов V выбрано так, как показано ранее, для того чтобы гарантировать непересекаемость блоков.

Общее число выводов в УЛМ шестого порядка может быть определено следующим образом: 6 выводов для основных входных сигналов, 16 выводов для выборки множества минтермов каждого из 16 блоков и 2 вывода для вспомогательных выходов Xl @ х2 и Xl @ х2. Общее число выводов в УЛМ шестого порядка, таким образом, равно 24 (исключая вывод для выходного сигнала). УЛМ десятого порядка с 228 выводами может быть получен при использовании аналогичного метода [27]. Подобная же техника использована Паттом [25] для получения УЛМ девятого порядка со 125 выводами и УЛМ десятого порядка с 225 выводами.

6.1.5. ГРАНИЧНЫЕ ЗНАЧЕНИЯ ЧИСЛА ВЫВОДОВ

Нижняя граница числа выводов, требуемых в УЛМ п-го порядка с одинарными или парафазными входами, может быть определена на основе рассмотрения числа различных комбина-

ИЛИ определения оптимальных разбиений. Однако если сконструирован один блок разбиения, удовлетворяющий условию избирательности множества вспомогательных функций, то остальные блоки могут быть построены на основе ранее рассмотренного метода.

Преперата [27] показал, каким образом могут быть использованы функции Xi@Xj и Xi@Xj в качестве вспомогательных. Рассмотрим следующую матрицу, которая определяет блок разбиения множества минтермов щести переменных:

гО О О О О От

О

logs (2ft-1-2) H-Iog2(ft-f 1)

Уменьшение граничного значения числа выводов может быть получено путем применения конструктивного метода с использованием разбиений, рассмотренного ранее. Число выводов для входных сигналов может быть минимизировано путем минимизации числа блоков при разбиении. Это требует максимизации числа минтермов в блоке. Блок с s строками должен иметь по крайней мере (1/2) (2* - 2) столбцов, так что любое целое число в интервале 1 2 - 2 представляется некоторым столбцом или его обратным кодом. Таким образом,

п>1(2-2), 2 <2п + 2,

s < log2 (2п + 2) = 1 + log2 {п + 1).

Следовательно, /[2 /(1 +log2(n-b 1))], где f -число блоков разбиения. Нижняя граница числа выводов m для входных сигналов, требуемых для УЛМ на п переменных, задается выражением

14-1оГ(п+1)-

Для больших п эта нижняя граница достигает общей оценки нижней границы, вычисленной ранее,

ционных функций и переменных и числа различных вариантов соединения входов. Пусть число выводов для входных сигналов в УЛМ равно m и пусть УЛМ имеет два указанных выше парафаз-ных выхода. Общее число функций л переменных равно 2 . Поскольку получаются как функции, так и их дополнения, то только половина этих функций должна получаться на одном выводе выхода УЛМ. Если предполагается наличие парафазных входов, то каждый из т выводов для входных сигналов может быть соединен с любой входной переменной, ее дополнением, нулевой или единичной шиной. Таким образом, число способов соединения каждого вывода равно 2п + 2, а общее число способов со-бщинения входных сигналов с т выводами равно (2п4-2) . Для того чтобы можно было реализовать все функции п переменных, число т должно удовлетворять неравенству

{2п + 2Г > 2(2 -1).

Следовательно,

mlog2(2n + 2)>2 -l, 2 1 2 - 1

Рис. 6.5. Граничные значения числа выводов УЛМ. с - УЛМ -ГО порядка с одинарными входами; б - УЛМ я-го порядка с одним парафазным входом; в - УЛМ п-го порядка с парафазными входами; г - УЛМ /г-го порядка с соединениями между выводами.