НО любое из этих двух дополнительных ограничений означает, что /(2,1) =f(3,1) и f(l, 1) =f(4,1). Следовательно, /-цепь (14/1, 23/1) не может быть исключена, и поэтому мы не можем определить какую-либо двоичную функцию f(Q, /) на М, которая была бы функцией обратной связи. Однако таблица состояний М' (рис. 5.39) является эквивалентной М (в предположении, что выходные функции подходящим образом определены) и может быть реализована с использованием функции f{Q, I) в качестве функции обратной связи, как показано на рисунке, /-цепь генерируется одним или двумя циклами состояний из диаграммы состояний. Для таблицы М, приведенной на рис. 5.38, /-цепь (12/0) генерируется одиночным циклом состояний (1/0, 2/0), тогда как /-цепь (12/1, 34/1) генерируется двумя циклами (1/1, 3/1) и (2/1, 4/1). Таблица М' (рис. 5.39) получена путем расширения таблицы М таким образом, чтобы расширить цикл состояния (1/0, 2/0) из М до цикла (1/0, 270, Г/О, 2/0). При большем увеличении длины цикла /-цепи могут быть исключены за счет бинарной функции f. Это может выполняться систематически в целях получения бинарных значений функции обратной связи таблицы М', эквивалентной любой таблице М [4].

5.6.3. ИСПОЛЬЗОВАНИЕ ВЫХОДНОЙ ФУНКЦИИ В КАЧЕСТВЕ ФУНКЦИИ ОБРАТНОЙ СВЯЗИ

Разработанные и описанные в предыдущем разделе методы могут быть также применимы для реализации таблицы состояний М, использующей, если это возможно, свою выходную функцию Z в качестве функции обратной связи. Если импликационный граф М, использующий функцию Z как функцию обратной связи, не содержит контуров, то по лемме 5.18 таблица М может быть реализована с использованием своей выходной функции Б качестве функции обратной связи. Однако если импликационный граф М имеет /-цепи и функция Z является частично неопределенной, то представляется возможным использовать расширение таблицы состояний для того, чтобы исключить /-цепи, что приводит в результате к таблице М', эквивалентной М в отношении выходной функции Z. Следовательно, Z. (9., /) =

= Zj (, /) Б УИ только в том случае, если функция Zj (qi, Im) является неопределенной в М.

Рис. 5.39. Эквивалентная таблица состояний с бинарной функцией обратной связи, пример 5.17.

Тест-граф для последовательностной функции с выходной функцией Z состоит из узла для каждой пары отличных друг от друга состояний из М и дуги, помеченной 1а, идущей от узла к узлу (q-p,qr), если N{qi,Ia) =Чр, N(qjJa)=qr, или наоборот и Z{qi, 1а)= Z{qj,Ia)- Тест-граф для М идентичен импликационному графу М с функцией Z в качестве функции обратной связи в том случае, если функция Z является полностью определенной.

Теорема 5.4. Последовательностный автомат М может быть реализован с использованием своей выходной функции в качестве функции обратной связи тогда и только тогда, когда его тест-граф не- содержит контуров.

Доказательство. Необходимость. Предположим, что тест-граф содержит контур. Тогда имеется последовательность входных сигналов, которая переводит М из состояния qi в qi к из состояния qj, (/ Ф i) в q с той же самой полностью определенной выходной последовательностью. Для любого автомата М', эквивалентного М, одна и та же входная последовательность (или входная последовательность, повторенная несколько раз) будет переводить М т q. в q и из q. в q с идентичными выходными последовательностями. Следовательно, тест-граф для М' содержит контур и, таким образом, М' не может быть реализован с использованием своей выходной функции в качестве функции обратной связи.

Достаточность. Доказательство требует более подробного объяснения процесса расширения таблицы состояний [4] и поэтому не может быть включено в данную работу. Основной поо-цесс иллюстрируется примером 5.18.

Пример 5.18. Тест-граф из таблицы состояний М, представленной на рис. 5.40, а, использующий выходную функцию в качестве функции обратной связи, показан на рис. 5.40,6. Пунктирными линиями указаны дуги, которые могут присутствовать (а могут и не присутствовать) в данное время, в зависимости от того, как проводится определение неопределенных ранее выходов^ Для исключения /-цепи (14/0) мы определяем Z(4,0) = = Z(1,0)= 1. Аналогичным образом, /-цепь (23/1) может быть исключена с помощью определения 2(2, 1) = Z(3, 1) = 1. Это полностью определяет Z и приводит в результате к импликационному графу, показанному на рис. 5.40, в.

Для того чтобы исключить /-цепь (12/1, 23/0), расширим таблицу таким образом, чтобы образовалась цепь (2/1, 3/0), так как выход Z для перехода 2/1 является неопределенным. (Порождающая цепь (1/1,2/0) не будет расширена, так как она не содержит переходов с неопределенным выходом Z). Расширенной цепью является цепь- (3/0, 271,370,2/1). Результирующая таблица и импликационный граф показаны на рис. 5.41,

р

О

. --Мм

у

Г*® ©

о

6

Рис. 5.40. Таблица состояний (а); тест-граф (б); тест-граф после определения z из примера 5.18 (в).

а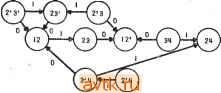

22 )*- 33

©00

Рис. 5.41. Расширенная таблица состояний (а); импликационный граф, пример 5.18 (б). . т

Комбиноцион-

тгтестя цепь

Рис. 5.42. Реализация обратной связи в виде сдвигового регистра.

Можно легко показать, что не любой автомат реализуется с помощью такого регистра. Рассмотрим таблицу М с тремя входными столбцами /ь /г, /з и состоянием qu таким, что N(quli), N{quh) и N{quh) все отличаются друг от друга. Если М реализуется с помощью сдвигового регистра с обратной связью, то для любого кода, присвоенного qu цепь, показанная на рис. 5.42, может перейти в одно из трех возможных последующих состояний. Но из рис. 5.42 очевидно, что последующие состояния, связанные с любым кодом, могут отличаться только Б г/1 и, следовательно, для любого состояния может быть только два различных следующих состояния. Ниже будет показано, что существуют также автоматы с двумя входными столбцами, которые не реализуются с помощью сдвиговых регистров с обратной СВЯЗЬК),

Поскольку здесь отсутствуют /-цепи и наиболее длинное звено имеет четвертый порядок, то пять последовательных значений Z и входной сигнал определяют текущее состояние N1 (которое является эквивалентным М) и М' может быть реализована с Z в качестве функции обратной связи. (Заметим, что если Л^(3,0) = 2, то три последовательных значения Z и входной сигнал определят текущее состояние М'.)

5.6.4. РЕА.ЛИЗАЦИЯ ОБРАТНОЙ СВЯЗИ В ВИДЕ СДВИГОВОГО РЕГИСТРА

В этом разделе рассматривается задача реализации заданной таблицы состояний в виде цепи, показанной на рис. 5.42. Такая реализация будет рассматриваться как реализация в виде сдвигового регистра с обратной связью. В отличие от реализаций, описанных выше, на вход поступает только текущий входной сигнал.

Лемма 5.19. Не все таблицы состояний с двумя столбцами могут быть реализованы с помощью сдвиговых регистров с обратной связью.

Доказательство, Рассмотрим таблицу М, приведенную на рис. 5.43. Заметим, что каждое состояние имеет два различных между собой следующих состояния, каждое из которых равняется текущему состоянию. Теперь .допустим, что М реализуется с помощью сдвигового регистра с обратной связью, причем сдвиговый регистр имеет длину п разрядов. Рассмотрим код (О, О, О,..., 0). Из рассмотрения цепи, изображенной на рис. 5.42, видно, что кодами возможного следующего состояния, связанными с этим кодом, являются (О, О, О,..., 0) и (1,0, О, О,..., 0). Если код, содержащий все нули кода, присвоен состоянию 1 (или 2, или 3), то одно из возможных следующих состояний для 1 (или 2, или 3) должно быть 1 (или 2, или 3). Таким образом, этот код не может быть связан с произвольно выбранным со-стоянием. Теперь рассмотрим код (О, 0,0,... Рис. 5.43. Табли-..., О, 1). С этим кодом предположительно ца. состояний, не можно связывать следующие состояния, имею- реализуемая с по-

/л г, rv г\\ /1 п л Г1\ IT мощью сдвиговых

щие коды (О, О, О,..., 0) и (1,0, О,..., 0). Но регистров с обрат-код, содержащий все нули, связан не с любым ной связью, произвольно выбранным состоянием. Следовательно, код (О, О, ...,1) действителен только для одного возможного следующего состояния и поэтому код (0,0,0,...,!) также не может быть связан с поризвольно выбранным состоянием. Повторяя последовательно аналогичные рассуждения, можно показать, что существует такой код, который мог бы быть присвоен любому состоянию, и, следовательно, таблица М не реализуется с помощью сдвиговых регистров с обратной связью.

Если мы ограничиваемся единственным кодом на состояние, то это упрощает получение некоторых необходимых условий для реализуемости с помощью сдвиговых регистров с обратной связью. Применительно к рис. 5.42 переменная yi определяет разбиение Гу, содержащее два блока. Определим R{n) следующим образом. При заданном разбиении л, Я{л) является наименьшим разбиением, таким, что если qi = qj{n) и существуют входы 1а, h, такие, что N{qi,Ia) = qm. N{qj,Ib) = qn, тогда qm = qn{R{n)). Теперь следующая лемма предоставляет нам возможность проверить заданное разбиение Ху, для того, чтобы определить, когда оно может быть использовано для порождения реализации в виде сдвигового регистра с обратной связью при однозначном кодировании.

Лемма 5.20. Двухблоковое разбиение л состояний из таблицы М при однозначном кодировании может быть использовано для реализации цепи в виде сдвигового регистра с обратной связью тогда и только тогда, когда Л] lTf=iP(jti) =0 для

некоторого конечного k, где Р* (яО = R (Р'~ (л,)) и R (лО = R (лх).

Доказательство. Необходимость. Если переменная yi определяет Л1, то у2 определяет разбиение л такое, что Л2Р(л1). (Выполните в качестве упражнения.) Аналогичным образом, г/з определяет разбиение Лз, такое, что ЛзР(л2). Повторяя эту процедуру, получаем yt, которое определяет разбиение Яг Р'~ (Я]). Следовательно, для кодирования состояний должно

быть справедливо Лх Yli=iR(щ) =

Достаточность. Если Лх - разбиение, содержащее два блока, то тогда, например, имеются Р (яО, R{ni) и т. д. Таким образом, MHOHtecTBo разбиений {я1, Р'(я1), i - l, k) может быть использовано для того, чтобы определить кодирование состояний. Допустим, что Я1 имеет блоки Bq, Bi, и определим переменную г/ присвоением кода yi = 0 этим состояниям в Bq и кода yi - 1 этим состояниям в В^. Теперь R (я имеет два блока Bq и В\, таких, что для любого е В^, q е В^, N [q, /) е Bq и (9, /) е В[ (или наоборот) для всех входов Если закодировать у^ так, чтобы все элементы из Во имели г/2 = О и все элементы из Bj имели у^- \ (или наоборот),

то У2 = г/1- Повторяя эту основную процедуру для /?( i), г=2, , получаем кодирование состояний, которое приводит к реализации в виде сдвигового регистра с обратной связью. Комбинационная цепь, реализующая функцию возбуждения, может быть получена из У-матрицы.

Таким образом, мы имеем тест для того, чтобы определить, может ли быть использовано разбиение Я] при однозначном кодировании для получения реализации в виде сдвигового регистра с обратной связью.

Лемма 5.21. Двухблоковое разбиение Я1 для состояний из таблицы М при однозначном кодировании может быть использовано для получения реализации в виде сдвигового регистра с обратной связью из М тогда и только тогда, когда а) N {qi, /J ф N {qt, h) (щ), если {qi, /J Ф N {qi, 1), б) qi==qf (я,), если N {qi, = N (q h).

Доказательство: a) Предположим, что N {qi, /J = N {qj, 7,) (Я1). Тогда Af(9j,/a) = Af(9t,/ft)(Р^)(я1)) для всех k. Следовательно, Я| ni =Р'(я,) =5 О и согласно лемме 5.20 ЯJ не порождает реализацию в виде сдвигового регистра с обратной связью.

б) Предположим, что qi ф qj (щ). Тогда из цепи, показанной на рис. 5.42, следует, что N {qi, /J и N{qj, I ) отличаются в у2, так как qi и q, отличаются в г/,. Это противоречит однозначному кодированию состояний, если N{qi, Ia)~N{qj, /J.

Пример 5.19. Сделаем попытку при однозначном кодировании состояний найти реализацию в виде сдвигового регистра с обратной связью для таблицы приведенной на рис. 5.44. Из леммы 5.21 следует, что порождающее разбиение л должно удовлетворять следующим ограничениям. 2=56(зт), 3=75(зт), 1=2(л), 4 = 5(зт). Разбиениями, содержащими два блока, удовлетворяющими этим ограничениям, являются только Л1 = (1245,36), и гт2==(123,456). Имеем Р (гп) = (2356, 14), Р^{л1) = /. Следовательно, jti не порождает реализацию в виде сдвигового регистра с обратной связью. С другуой стороны, Н{Л2) = = (126,345), P2(j2) = (246, 135). Следовательно, Л2 порождает такую реализацию, так как гт2-Р(зт2) (лг) = 0. Если мы присвоим код yi = О состояниям 1,2,3, то затем присвоим код 2 = 0 состояниям 1, 2, 6 (так как блок Во= 123 из Я2 отображается в блок Во = 126 из Н{л2)) и г/з = О состояниям 2, 4,6.

Полное кодирование состояний показано ниже.

Рис. 5.44. Таблица состояний из примера 5.19.

Ух У2 Уз

2 3 4 5 6

О О 1 1 1 О

О

о

Затем из У-матрицы, приведенной на рис. 5.45, получается комбинационная цепь, реализующая функцию возбуждения. Следующее состояние определяется такими уравнениямиз

Yl = хуз + ху2Уз + хууз -f- г/,2. У2-==Уи

Уз == У2-

Рис. 5.45. У-матрица при реализации обратной связи с помощью сдвигового регистра, пример 5.19.

Рис. 5.46. Таблица состояний из примера 5.20.

кодов для некоторых состояний. Ограничения из леммы 5.21 должны быть удовлетворены посредством выбора щ так, чтобы

1-Ш=1Ы = 0.

Пример 5.20. Для таблицы, приведенной на рис. 5.46, разбиение п, которое может породить при однозначном кодировании реализацию в виде сдвигового регистра с обратной связью, должно удовлетворять следующим ограничениям: 1фЗ{п), 25(я), 2=56(jt), 1=54(я), 1=5=6(jt), 2=3=4(я). Разбиением, которое удовлетворяет этим ограничениям, является только Л1= (156,234). Если R{n) ограничено разбиением, то R{ni)=: = (134,256) и R(л\) = 1. Следовательно, Jti не порождает при однозначном кодировании реализацию в виде сдвигового регистра с обратной связью, т. е. реализация отсутствует. Однако если R(n) не ограничивается разбиением, то /?(я;) = (134,256) и R(ni) = (1236,1245). В этом случае ni-R{ni)-Rim) = 0.

Таким образом, п\ порождает реализацию таких регистров посредством следующего не полностью определенного однознач-

Уравнения для Кг и Уз ясно указывают, 4to возможна реализация в виде сдвигового регистра.

Если устранить ограничение о том, что R(n) есть разбиение, то лемма 5.20 все еще является достаточной для реализации в виде сдвигового регистра с обратной связью и это предоставляет нам возможность найти некоторые такие реализации в виде сдвиговых регистров, которые требуют присвоения многих

Реализации последовательностиыи автоматов 343 НОГО кодирования состояний:

Комбинационная цепь получается из У-матрицы, показанной на рис. 5.47.

к, = X, 2 Уг + Хг у, \з + х, д: Уг + ji У] >2 h Уг = У, Уз = Уг

Рис. 5.47. У-матрица при реализации обратной связи с помощью сдвигового регистра, пример 5.20.

Рис. 5.48. Таблица состояний из примера 5.21.

Однако если R{n) не ограничивается разбиением, то лемма 5.20 не дает необходимых условий реализации с помощью сдвигового регистра с обратной связью, что иллюстрируется следующим примером.

Пример 5.21. Для таблицы, показанной на рис. 5.48, не имеется разбиения, которое удовлетворяет ограничениям леммы 5,21, а) и б), и, следовательно, не имеется реализации в виде сдвигового регистра с обратной связью при однозначном кодировании. Разбиениями, которые допускают ограничения из леммы 5.21, а), являются Jti=(14,235) и Л2= (13,245), R{ni)-l,

3 4 5

Рассмотрим это кодирование состояний и сравним его с кодированием состояний № 2, генерируемым яг, R{n), R{n),

Кодирование состояний № 2

У\ У2 Уз 10 0-

2 10 1

3 0 1-

4 11-

5 1-0

Частичное кодирование № 2 согласуется с кодированием № 1, где бы первое из них ни было определено. Однако кодирование состояний № 2 не является достоверным кодированием, гак как некоторые коды присваиваются более чем одному со> стоянию. Например, состояния 4 и 5 оба имеют код 110. Кодирование состояний № 1 для сдвигового регистра может быть получено из кодирования № 2 путем добавления переменной yi (не полностью определенной), а идентификация некоторых неопределенных состояний приводит, вообще говоря, к многозначному (а не полностью однозначному) кодированию состояний. Это делается следующим образом.

Допустим, что какой-либо из кодов, присвоенных состоянию 2 в кодировании состояний № 2, должен быть выбран, как для этого состояния, при улучшенном кодировании. Так как Л/(2, 0) = = N{2,1) =5, если код 101- присваивается состоянию 2 npi

R{n2) = (125,345), РЦп2) = (1345,1234) и ЯЦп2) = I. Таким образом, ни Яь ни яг не удовлетворяют условию леммы 5.20. Однако имеется кодирование состояний № 1, которое дает возможность при многозначном кодировании получить реализацию с помощью сдвигового регистра, в котором yi определяется яг.

Кодирование состояний № 1