1-1-1

Рис. 5.29. Обобщенная реализация, не имеющая обратных связей.

на рис. 5.29, где С{ являются комбинационными цепями, а

X -число входов. Для этой цепи Цт,. =0 для у У2, J/fc

в целях определения правильного кодирования состояний.

Ху, >т{1), Ху, >т{хуХ Ху >т(т^, Ху,) = т(ху,) = (I) и вообще

Ху.тЧГ). Следовательно, если Дт. =0, то т^(/) = 0.

Комбинационная логическая непь

Рис, 5,30. Цепь,: не имеющая обратных связей.

Достаточность. Допустим, что №)(/)= О для таблицы А. Тогда для любой пары состояний <?, и и любой входной последовательности x длиной k N{qi,X) =N(qj,\). Следовательно, k последующих входов являются достаточными для того, чтобы определить следующее состояние и, следовательно, выход А. Отсюда следует, что А может быть реализована цепью без обратной связи, показанной на рис. 5.30.

деления событий или таблицы определения автомата. Состояние определения автомата представляет собой функцию конечного числа предшествующих входов. Число требуемых для определения состояния предшествующих входов назьшается степенью определения события.

Лемма 5.16. Таблица состояний А может быть реализована без обратной связи (при использовании D-триггеров в качестве элементов памяти) тогда и только тогда, когда т'(1) =0 для некоторого конечного k, где m(l) ~т{гФ-{1)) для всех k>\ и т>(/) =т{1).

Доказательство. Необходимость. Допустим, что А может быть реализована без обратной связи. Большинство реализаций, не имеющих обратной связи, обычно такие же, как это показано

Пример 5.14. Для таблицы, представленной на рис. 5.31, а, /п(/) = (123,4), /п2(/) = (12, 3, 4), тЦ1) = 0.

Следовательно, три последних входа определяют текущее состояние, и автомат может быть реализован без обратной связи.

о

О О

1 1 о о 1 1 о о 1 1

о

о о 1 1 1 1 о о о о 1 1 1 1 о о

2 3 3 4 4 4 4 4 4 4 4 3 3 2 1

О 1 О

о 1 1 1 1 о о о о 1 1 о о

Рис. 5.31. Таблица состояний из примера 5.14 (а); Z как функция х, Xi

Хъ Хз (б).

Таблица, представленная на рис. 5.31,6, определяет текущее состояние q как функцию (комбинационную) трех предшествующих входов, а выход г-как функцию текущего и предыдущих

ноя логическая цепь

Рис. 5.32. Реализация, не имеющая обратных связей.

входов. Текущий вход обозначается х, а вход при t - i соответственно Xi.

Автомат, который может быть реализован без обратной связи, показан на рис. 5.32. Комбинационная цепь, вычисляемая на основе таблицы, представленной на рис. 5.31,6, определяется согласно

Z = XXXz + XXi -f XXiX.

5.6.2. РЕАЛИЗЛЦИИ С ОДНИМ КОНТУРОМ ОБРАТНОЙ СВЯЗИ

При реализации последовательностной функции, использующей элементы задержки в качестве памяти, индекс обратной связи цепи представляет собой минимальное число ветвей, которые должны быть рассечены для осуществления прерывания всех замкнутых контуров. Вообще говоря, различные реализации одной и и той же последовательностной функции могут иметь различные индексы обратной связи.

В этом разделе будет рассматриваться реализация последовательностной цепи с наименьшим возможным индексом обратной связи для произвольной (синхронной) таблицы состояний.

*{д}-гН1]---р[1}

Комбинационная логическая цепь

Рис. 5.33. Последовательностная цепь с функцией обратной связи f.

По результатам предыдущего раздела можно определить, может ли таблица быть реализована с нулевым индексом обратной связи. Теперь докажем, что любая таблица состояний, которая не может быть реализована таким образом, может быть реализована с единичным индексом обратной связи канонической цепью, показанной на рис. 5.33, где / представляет собой бинарную функцию. (На этом рисунке каждая входная линия, представляемая х, подается на сдвиговый регистр из п задержек.)

Теорема 5.4. Любая (конечная) таблица состояний может быть реализована как синхронная последовательностная цепь с единичным индексом обратной связи.

Доказательство. Предположим, что М - таблица, которая должна быть реализована, содержит р состояний. Поскольку мы попытаемся реализовать М с одним контуром обратной связи, мы должны передать обратно информацию о состоянии М с помощью последовательности т разрядов, где tn [log2p]. Таким образом, мы можем передать обратно новую информацию о состоянии М через каждые т единиц времени. Однако

1 mil w 1

Комбинационная логическая цепь

Рис. 5.34. Каноническая реализация с одним контуром обратной связи.

привести цепь в такое положение, при котором состояние первой (левой) половины f-сдвигового регистра определяет состояние М на время t - т, а последние (по отношению к времени t - т) т входных сигналов запоминаются в первой половине х-сдвигового регистра. Эта информация является достаточной для того, чтобы определить состояние М на момент времени / и выход М. Для следующих т единиц времени, пока коды состояния к моменту t - т сдвигаются во вторую (правую) половину /-регистра, входные состояния запоминаются, а т разрядов, которые единственным образом определяют состояние М на момент времени t, вырабатываются комбинационной цепью С и подаются в первую половину f-регистра, по одному разряду за определенный интервал времени. (Для того чтобы выполнить эту процедуру, необходимо знать местоположение разрядов, ко-

ПО истечении некоторого промежутка йремени мы можем запомнить псе последующие входы. Эта входная информация позволит сформулировать соответствующий выходной сигнал, дающий информацию о следующем состоянии в течение данного интервала времени.

Рассмотрим цепь, показанную на рис. 5.34. Предположим, что некоторым способом в течение интервала времени t можно

) Состояние qi из таблицы М является переходным, если qi не появляется в качестве содержимого следующего состояния в М или qi появляется в качестве содержимого следующего состояния только в строках, предста^-/!яющих переходные состояния.

торые определяют состояние М на момент времени t - т, по мере того, как они сдвигаются, и по мере того, как сдвигается новое кодовое слово. Затем к моменту времени t -\- т необходимо запомнить код, который определяет состояние М на момент времени t, в первой половине f-регистра и последние т входов запомнить в первой половине х-сдвигового регистра, возвращая, таким образом, цепь к ситуации, аналогичной той, с которой начинался ее запуск. Одним из тех кодов, который может быть использован в этой процедуре, является код, при котором каждому состоянию <?,-, t=l, р, ставится в соответствие код длиной т = р \, состоящий из i единиц, следом за которыми идут т - i нулей. Кодовое слово состояния вначале сдвигается нулями. Отсюда положение этого кодового слова в сдвиговом регистре единственным образом определяется последовательностью из т разрядов, из которых левые старшие i разрядов равны единице, а следующие m - i разрядов равны нулю. Если в некоторый момент времени кодовое слово состояния начинается в -разряде f-регистра, то 1) разрядов следующего кодового слова состояния уже были поданы и f принимает значение следующего разряда в этом кодовом слове, как это определяется текущим кодовым словом состояния в разрядах от <? до + и последними значениями [q + т) входов, которые запомнились в разрядах от 1 до {q -т т) регистра х. Определение местополон<ения кодового слова и значения следующего разряда этого слова производится с помощью текущего кодового слова состояния в разрядах от до [q + т) и последними

--т)-значениями входов, которые запомнились в разрядах от 1 до {q -\- т) регистра х. Определение местоположения кодового слова и значения следующего разряда, который должен быть передан по цепи обратной связи, может потребовать использования сложной комбинационной функции.

Для любого непереходного') состояния qi имеются состояние qj и входная последовательность X длиной т, которая будет переводить М из qj в <?,-. При установке цепи в начальное состояние qi код для q, запоминается в первой половине f-регистра, а входная последовательность Х ,- сдвигается в первую половину х-регистр а. Все другие регистры устанавливаются в нуль. При установке цепи в переходное состояние(7 мы запоминаем код для q\ в регистре Т и устанавливаем все другие регистры в^ нуль. В течение следующих т единиц времени код для q подается в f-регистр по одному разряду за один такт

путем определения f = Тт (т-й разряд из т), и нули сдвигаются в Г-регистр.

Код, использованный при доказательстве теоремы 5.4, оказывается не очень эффективным. Действительно, могут быть выбраны коды, для которых т аппроксимирует Floggpl при больших значениях р. Конструктивное доказательство теоремы 5.4 дает каноническую реализацию с одним контуром обратной связи для любой таблицы. Однако для большинства таблиц могут быть найдены значительно более экономичные реализации.

Лемма 5j7. Таблица состояний М может быть реализована с использованием функций f(Q,/)) для М в качестве функции обратной связи тогда и только тогда, когда текущее состояние М определяется последними -значениями входа и функцией f(q,i) для некоторого конечного п.

Доказательство. Аналогично доказательству леммы 5.16 (выполните в качестве упражнения).

Если таблица состояний М имеет функцию f{q,l), которая удовлетворяет условиям теоремы 5.4, то М может быть реализована цепью, показанной на рис. 5.34. Поскольку обрыв ветви, помеченной f, будет исключать все замкнутые ветви, то f может быть названа функцией обратной связи для цепи, и если количество отличных друг от друга значений в диапазоне f равняется k (т. е., / является -значной функцией), то индекс обратной связи этой цепи может быть меньшим или равным [logal, где [х\ является наименьшим целым х.

Теперь рассмотрим задачу определения функции обратной связи для заданной таблицы состояний. Импликационный граф таблицы состояний М для функции f(q,i) состоит из

1) узла для каждой пары различимых между собой состояний qi и qj {i <; /) автомата М,

2) дуг, определенных следующим образом.

Положим, что f{qm,lh) представляет собой значения функции /, когда текущим состоянием является qm, а входом - ih-Тогда если N{qi,ia) = qp и N{qj,ia) = qr qp и f{qi,ia) и f(Q}, la) не определяются по другому, то имеется направленная дуга, помеченная / , от узла (<?г, <?j) к узлу {qp,qr), и аналогично, если N(qi, / ) = <?г и Л/(<?,-, / ) = <?р.

Импликационный граф М для полностью неопределенной функции f{q,i) будем называть универсальным импликационным графом. М. Таким образом, этот граф будет иметь дугу из iQuQi) к (<?р,<?г), помеченную / , если N{qi,ia) = qp, N{qj,ia) = = qr или N{qi, h) = <?r, (<?j. h) - qv

) Функция j(Q,I) зависит от состояния и входа Af,

Контур порядка k является замкнутым направленным графом, состоящим из k дуг (не обязательно отличающихся друг от друга). Если при движении по графу траектория не проходит через какой-нибудь узел больше чем один раз, то такой контур называют элементарным. Контур импликационного графа будем иногда называть /-цепью.

Звено порядка k является совокупностью k отличных друг от друга дуг и проходящих через k + 1 разных узлов точно один раз (считая узлы исходной и конечной части траектории).

/-цепь, состоящая из узлов (в последовательности (ti, /О;

/2), . (ffe/ft)) и дуг, помеченных (в той же самой последовательности) If (от (fVi)). h--ih будет обозначаться

{hhlij hhlh---> kkh Звено будет обозначаться аналогично, но правая скобка должна быть заменена квадратной скобкой.

Пример 5.15. На рис. 5.35, а показаны таблица состояний и функция обратной связи f(Q,I). Содержимым таблицы является следующее состояние и функция обратной связи. Импликационный граф показан на рис. 5.35, б.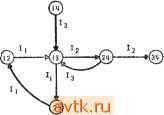

Рис. 5.35. Таблица состояний и функция обратной связи (а); импликационный

граф (б).

Лемма 5.18. Таблица состояний М может быть реализована с использованием функции f{Q,I) как функция обратной связи тогда и только тогда, когда импликационный граф М для(С,/) не имеет элементарных цепей.

Доказательство. Необходимость. Предположим, что импликационный граф имеет элементарную цепь порядка k (iJJIt

hhlh, hhlh соответствии с леммой 5.17 если f{Q,I)

является обратной функцией для М, то должно быть некоторое конечное п, такое, что текущее состояние М зависит только от последних п значений входов и функции /. Но для всех п > О

ti, h, It, It, It, .... It,, It It, ha,

a последними n значениями функции f{Q,I) являются

f {ii,It,), f{ik, It, f{h. It,), !{ia ha,).

Тогда из определения импликационного графа следует, что если начальное состояние было н или /ь то текущее состояние могло быть г'д^, или ]а,+у Следовательно, по лемме 5.17 f{Q,I) не является для М функцией обратной связи.

Достаточность. Допустим, что на импликационном графе отсутствуют элементарные цепи и что наиболее длинное звено имеет порядок k. Допустим также, что для некоторой последовательности k предыдущих входов и значений функции f{Q,I) текущее состояние могло быть Qi или для i 4= / Тогда для любого входа / либо f{qi, Im)¥=f(qj, Im), либо N(qi, Im) = = N{qj,Im) или, кроме того, импликационный граф функции f{Q,I) на М должен иметь звено порядка k-\-l. Поэтому k+ 1 последовательных предыдущих значений входа и функции f(Q,/) определяют текущее состояние М и, следовательно, по лемме 5.17 функция f(Q,I) является для М функцией обратной связи.

Следствие 5.2. Сокращенная таблица состояний М может быть реализована с нулевым индексом обратной связи тогда и только тогда, когда на универсальном импликационном графе для М отсутствуют элементарные цепи.

Импликационный граф может быть полезным при определении функций обратной связи следующим образом. Процедура 5.3

1. Строим универсальный импликационный граф для заданной таблицы состояний М.

2. Если на таком графе отсутствуют элементарные цепи, то определяем функцию f(Q,I) таким образом, чтобы устранить выбранные дуги и, следовательно, элементарные цепи. Дуга из узла (qi, qj), помеченная / , удаляется с помощью надлежащего выбора f{qi,Ia) и fiqj,Ia). Если f является бинарной функцией, то это эквивалентно f{qi,Ia) = f{qj,Ia).

3. Повторяем шаг 2 до тех пор, пока все (элементарные) цепи не будут удалены из графа.

Пример 5.16. Задана таблица состояний, представленная на рис. 5.36, с. Универсальный импликационный граф показан на

п ~ aik + й2, где й! О и О Ог < . Допустим, что последними п входами являются

повторяется ai раз последние а% входов

о

Рис. 5.36. Таблица состояний из примера 5.16 (а); универсальный имглика-

ционный граф (б).

И б. Поскольку наиболее длинное звено импликационного графа имеет единичный порядок, два последовательных значения f и X определят текущее состояние М, как показано на рис. 5.37, в. Функция обратной связи может быть вычислена в виде

f{t)x(t)x(t-l)x{t-2)f(t-2) + x{t)x(t-l)x{t-2) +

+ x{t)x{t-l)f{t-l)-\-x{i~l)f{t-l).

Однако процедуру 5.3 не всегда можно использовать для реализации последовательностной функции с обратной связью, имеющей единичный индекс.

Пример 5.17. Задана таблица состояний М, показанная на рис. 5.38. Универсальный импликационный граф показан на рис. 5.38, б.

Вначале ограничим функцию f(Q,/) так, чтобы исключить /-цепи единичного порядка, например, следующим образом: f(l,0) =:f(2,0); /(3,0) =f (4,0); f (1, 1) = f (3,1); f (2,1) = = f(4,1). Для исключения /-цепи (12/1,34/1) следует ограничить / таким образом, чтобы /(1,1) = f{2, 1) или f{3, 1) = f(.4, 1),

рис. 5.36, б. Устраним все элементарные цепи из-за следующих ограничений на функцию /:

f==(l, 0) = f (2, 0); fi2, l) = f (3, 1); f (2, 0)=f (4. 0).

Для того чтобы уменьшить длину наиболее длинного звена, установим f(3,1) = f(4,1). Вообще говоря, уменьшение числа ветвей импликационного графа будет приводить к увеличению неопределенности f{t) и Z{t), являющихся отображением выхода М, как функции от предыдущих значений выходов и значений f. Поэтому примем f{l, 1) = f{4, 1). Результирующая функция обратной связи и импликационный граф показаны на рис. 5.37, а

(g) ©

x{t - 2) x{t-l) f{t - 2) f(t - i) Текущее состояние

О О О

о о о о о

о о о о

о о I 1 1 1 о о о о 1 1 1 1 о о

о I 1 о о I 1 о о 1 I о о 1 1 о

3 4 1

Рис 5.37. Функция обратной связи (а); импликационный граф (б); состояние как функция предыдущих значений [ и х, пример 5.16 (в).

С1ч1 из)

Рис. 5.38. Таблица состояний из примера 5.17 (о); универсальный импликационный граф (б).