Рис. 5.5. Таблица состояний и не полностью определенное однозначное кодирование.

Применяя теорему 5.1, можно заключить, что не имеется такого однозначного кодирования для таблицы состояний, при котором некоторая переменная состояний является независимой от всех других переменных состояния. Однако при показанном на рисунке многозначном кодировании состояний (где состояние 4 имеет два кода 011 и 111), следующее значение состояния Yi зависит только от г/i.

Структурное упрощение, получаемое при таком кодировании, не было очевидным при рассматриваемых разбиениях. Для того чтобы систематически раскрывать такую структуру, необходимо расширить нашу алгебру разбиений до алгебры системных множеств.

Системное множество л на множестве S является совокупностью Вь Вг, ..., Bi из S, таким, чтоУгВ = 5 и BiBj для i ф /. Таким образом, разница между разбиением и системным множеством заключается только в том, что к указанным подмножествам Bj не предъявляются требования непересекаемости. Разбиение является особым случаем системного множества, а алгебра системных множеств в основном подобна алгебре

5 3 АЛГЕБРА СИСТЕМНЫХ МНОЖЕСТВ

ПРИ МНОГОЗНАЧНОМ КОДИРОВАНИИ СОСТОЯНИЙ

В то время как алгебра разбиений может быть использована для получения однозначного кодирования состояний с уменьшенной зависимостью (если это возможно), эта алгебра не всегда адекватна задаче получения реализаций с уменьшенной зависимостью, использующих многозначное кодирование состояний. Например, не имеется двух блоков разбиения со свойством подстановки для таблицы состояний, показанной на рис. 5.5.

разбиений. Определения О и 1 являются неизменными, а отношения и - являются простыми расширениями определения для разбиений.

Представляется удобным выделить два различных класса многозначного кодирования состояний. К первому классу относится множество кодов, присвоенных любому состоянию, которое может быть идентифицировано единственным кодом с некоторыми, возможно неопределенными, переменными, как показано на рис. 5.5. Будем рассматривать этот тип присваивания как не полностью определенное однозначное кодирование и сохраним выражение многозначного кодирования состояний при присваиваниях кодов, в которых некоторым состояниям присвоен более чем один код и которые не могут быть выражены как не полностью определенное однозначное кодирование. Например, такое кодирование с двумя переменными и тремя состояниями имеет код 00, присвоенный состоянию 1, код И, присвоенный состоянию 2, и коды 01 и 10, присвоенные состоянию 3.

В то время как полностью определенная переменная состояний соответствует двум блокам разбиения, не полностью определенная переменная состояний при однозначном кодировании соответствует двум блокам системного множества, в которых если состояние qi является неопределенным в переменной г/j, то qi появляется в обоих блоках Ху.. Ранее доказанные теоремы

остаются справедливыми для не полностью определенного однозначного кодирования, когда разбиения заменяются системными множествами. При этом представление о паре разбиения заменяется парой множеств при неизменных остальных определениях. Если не делается специальной оговорки,то рассмотренная ранее уменьшенная зависимость будет применяться к полностью определенным и не полностью определенным однозначным кодированиям состояний.

Для того чтобы найти реализации с уменьшенной зависимостью, необходимо проанализировать алгебраическую структуру данного автомата с тем, чтобы установить системные множества (разбиения являются их частным случаем) со свойством подстановки и пары множеств (или пары разбиений). (Для автомата с 2* состояниями, если мы хотим использовать кодирование состояний только с /г-переменными, необходимо ограничивать себя разбиениями.) Следующие леммы упрощают задачу нахождения таких системных множеств. Исключая оговоренные случаи, эти леммы являются справедливыми, когда задача ограничивается использованием разбиений.

Суммой двух системных множеств является наименьшее системное множество, большее или равное каждому из них. Формально заданные два системных множества щ и зтг, определен-

ные на множестве 5 как сумма ni + 3x2, являются таким системным множеством, что

а) зх, + 3X2>3Xi,

б) ЗХ] + Я2 2,

в) для любого другого системного множества щ, такого, что зхг>зх, и я,->Я2, имеет место

Следующая лемма, которая является аналогичной лемме 5.1, приводит к процедуре получения суммы двух системных множеств. Заметим, что эта лемма не является справедливой, если Я1,Я2 и jii +Я2 являются разбисниями.

Лемма 5.3а. Если щ и яг являются двумя системными множествами, определенными на множестве S, и qu q, то qi - = qjii + Я2) тогда и только тогда, когда

а) qi = qi(ni), или

б) 9, = 9j(3X2).

Доказательство. Аналогично лемме 5.1.

Таким образом, сумма двух системных множеств, определенная на множестве S, является системным множеством, содержащим все блоки т и П2, исключая блоки, которые содержатся в других блоках.

Следующая лемма может быть использована для получения суммы двух разбиений, когда сумма должна ограничиваться разбиением.

Лемма 5.36. Если щ и яг являются двумя разбиениями, определенными на множестве S, и qu qjS и если Я] + яг является разбиением, то qt = qj{ni + яг) тогда и только тогда, когда

а) qt = q] (щ или Я2) (т. е. q = q (щ) или qi = q, (щ),

б) существует такая последовательность q, Qk > Qk Qki

что

QiQkXi или я), Pkm = (я, или я,) к m < г - 1,

qk = Ql{i или я).

Доказательство. Выполните в качестве упражнения. Пример 5.4. Положим, Я1 = (12,34, 56), яг = (13,24, 56) и яз= (1,2,34,56).

я, я, == (1, 2, 3, 4, 56) = Я4; Я] Яз = Яз; Я2 Яз = я, Яг = Я4.

Интерпретируя зхь зхг и пз как системные множества, получаем

Я1 + зх2 = (12, 13, 24, 56) = 3X5, Я1 + Яз = (12, 34, 56)= я Я2 + Яз = (13, 24, 34, 56) = Яб.

Если зхг + щ является разбиением i, j = 1, 2, 3, то + Я2 = (1234, 56) = 3x7, я,+ 3x3 = (12, 34, 56) = я Я2 + Яз = (1234, 56) = Я7.

Частичное упорядочение яь яг и яз и их произведения и суммы, интерпретируемые как системные множества, показаны на рис. 5.6, а. Если они являются разбиениями, то представляющая их решетка показана на рис. 5.6, б. В обоих случаях m-Uj

Яг, Uj 3ti + Я^-.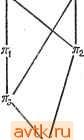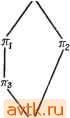

Рис. 5.6. Решетка из системных множеств (а); решетка из разбиений (б).

Поскольку пары множеств (и разбиений) являются полезными при построении кодов состояний с уменьшенной зависимостью, целесообразно рассмотреть проблему генерации пар множеств для заданной таблицы состояний. Приводимые рассуждения будут применимы к парам разбиения, так же как и к парам множеств, за исключением особых случ,аев.

Следующие две леммы показывают, как пары множеств могут быть определены из других пар множеств.

Лемма 5.4. Положим, что яь яг, Яз, Я4 являются системными множествами, определенными на множестве состояний S автомата М,

а) Если ЯзЯа и Р(я1, щ), то Р(я1, Яз).

б) Если Я4<Я1 и Р(я1, Яг), то Р{Щ,П2). Доказательство, а) Допустим, что Яз > Яг и Р(я1,Я2), но

(я1, Яз) не является парой множеств. Тогда должно существовать такое множество состояний А, что А(щ) (Л содержится в некотором блоке щ), N {А, Ik) {2) {N {А, Ik) содержится в некотором блоке Яг) для всех и для некоторого входа N (Л, 1т) не содержится в любом блоке Я3. Но это является невозможным, так как ЯзЯг, т. е. имеется противоречие. Следовательно, Р (яг, Яз).

в) Аналогично а). Выполните в качестве упражнения. Лемма 5.5. Положим, что яь яг, яз, Я4 являются системными

множествами, определенными на множестве состояний автомата М.

а) Если Р (я1, Яг) и Р (%, щ), то Р (я1 Яз, Яг Я4).

б) Если Р (Я], Яг) и Р (яз, Я4), то Р (я1 + Яд, Яг + Я4), за исключением случаев, когда М является не полностью определенным, а Я1, Яг, Яз, Я4, Я] + з и Яг-1-Я4 должны быть ограничены разбиениями.

Доказательство, а) Допустим, что Р (я Яг) и Р (яз, Я4), но (Я] Яз, Яг Я4) не является парой множеств. Тогда должно существовать такое множество состояний Л, что Л(я1-Яз) и (Л, Ik) не содержится в любом блоке Яг Я4 для некоторого входа Ik- Следовательно, N (Л, Ik) не содержится в каком-либо блоке Яг или N (Л, Ik) не содержится в любом блоке Я4. Однако, если Л (Я] Яз), то Л (я,) и Л(яз), и так как Р(я1, Яг) и Р(я з, Я4), N (Л, Ik) (3Х2) и N (Л, Ik) (3Х4), то получается противоречие. Следовательно, Р (я1 Яз, Яг Я4).

б) Аналогично, а). Выполните в качестве упражнения.

Часть б) леммы 5.5 не является справедливой, если Я] -Ь щ и Яг + Я4 должны быть разбиениями для не полностью определенных таблиц состояний. Рассмотрим таблицу, представленную на рис. 5.7. Если я, = (12,34), Я2 = (14,23), Яз = (13,24), Я4 = (1,23,4), тогда Р(я1,Я2) и Р(яз, Я4). Однако я,+ Яз = / = = (1234), а Яг+ Я4 = (14,23) и (я, + Яз, ЯгЯ4) не является парой разбиения. Однако для полностью определенных автоматов лемма остается справедливой при ограничении на разбиения. (Выполните в качестве упражнения.)

Будет полезным неформально ввести представление об информации о системном множестве. Системное множество яь определенное на множестве элементов S, может трактоваться как представляющее некоторую информацию о конкретном элементе из S в том смысле, что знание блока из я представляет знание элемента из S в пределах подмножества 5. Таким образом, если я= (123,345), то информация, представленная в я,

определяет конкретный элемент из 5 в возможном множестве {1,2,3} или множестве {3,4,5}. Алгебра множеств может быть затем использована для представления о потоке информации. А именно, для заданного автомата М, если зХ] и яг являются системными множествами со свойствами Р(щ,П2), то информация о текущем состоянии М, представленная посредством щ, и знание входа являются достаточными для вычисления информации, представляемой щ, о следующем состоянии М. Таким образом, для таблицы, показанной на рис. 5.8, так как Р(яь яг), где п\- (12,345) и Я2 = (123,45), если текущим состоянием является блок By = (12) из яь а входом является О, то следующим состоянием является блок fig = (45) из яг-

о I

о 1

2 3 4 5

4 5 I

Рнс. 5.7- Не полностью определенная таблица состояний.

Рис. 5.8. Таблица состояний.

Использование представления об информации, как следует из леммы 5.4а, приводит к тому, что если информация, заключенная в Пи является достаточной для определения информации, заключенной в яг, то при увеличении количества информации о текущем состоянии (т.е. Я4 яО мы можем еще определить информацию о следующем состоянии, заключенную в Я2. Аналогичным образом, лемма 5.46 означает, что мы можем также вычислить меньшую информацию о следующем состоянии (т. е. Яз Яг).

Для заданного автомата и системного множества я является естественным определить наибольшее количество информации о следующем состоянии, которое может быть получено из я, обозначаемом в терминах системного множества посредством т{я). Аналогично наименьшее количество информации о текущем состоянии, которое требуется для вычисления информации о следующем состоянии, представленном системным множеством я, может быть определено в тех же терминах, как М(я).

Формально для системного множества я, определенного на множестве состояний Q таблицы А,т{п) является таким системным множеством, что Р(п, т(я)), и если т является любым

другим системным множеством, которое обладает свойством Р(п,т), тот<};т(я).

Аналогично М{п) является таким системным множеством, определенном на таблице А, что Р(М{л),п) и если т' является любым системным множеством, которое обладает свойством Р(х',п), то т'>>М(л). Покажем теперь, что т{п) и М{п) являются единственными.

Лемма 5.6. Для системного множества л, определенного на множестве состояний Q автомата М, т{л) и М{п) являются единственными.

Доказательство. Предположим, что существуют два системных множества ti, Tg, таких, что Titg, TzTj, Р {п, ti) и Р (л, Тг), и для любого Tj, такого, что Р(л, т,), <); т Т; <]: Tj. По лемме 5.5а Р(л л, т, Tj). Если TjTj и тгт], то Tj < Ti и Т1Т2 < Т2, что противоречит допущению о и Tg. Следовательно, т(л) является единственным.

Доказательство для М (л) является аналогичным и оставлено в качестве упражнения.

Для системного множества л, определенного на множестве состояний Q автомата А, для каждого блока В, из л и каждого входного столбца из А существует блок из т(л), такой, что N{Bi,Ij)Bk. Следовательно, блоки из т(л) являются множествами N{Bi,Ij) для всех i и /, которые не содержатся в любом другом блоке. Если некоторый элемент из Q не содержится в любом из этих блоков, то это состояние один раз появляется в блоке из т(л).

Аналогично каждый блок В, из М(п) является таким, что N{Bi,Ij) Вп, где Bfe - блок системного множества л, а Ij - любой входной столбец. Кроме того, М(л) является наибольшим системным множеством, обладающим этим свойством. Определяя два состояния и qj как совместимые {qi ~ qj), если N(qk,Ik) = N{qj,Ik) (л) для всех 1, М{л) является множеством максимальных совместимостей, определяемых посредством соотношений совместимости.

Пример 5.5. Рассмотрим автомат, показанный на рис. 5.9, и системное множество л=(15,34,2). Системное множество т(л) состоит из блоков, соответствующих множествам содержимого следующего состояния из (15) и (34). Аналогично М(л), определяемое совместимыми парами, показано на графике, где Qi ~ qj, если N{qi,Ik) = N{qj,Iu) (л) для всех h.

Системными множествами являются

m (л) = (13, 25, 34), Л1(л)=(145, 2, 3).

Если m{ji) и М{п) являются разбиениями, то

т(я) = (134, 25) и М(я) = (145, 2, 3).

Если п является разбиением, а таблица состояний является полностью определенной, то М{л) будет разбиением. В этом случае легко вычислить М{п) без использования графика пар,

так как если qi qj и qt qk, то qu qj и qk могут быть все расположены в одном и том же блоке из М{п). Однако если л не является разбиением или если таблица состояний не является полностью определенной, то такое утверждение не будет истинным. При не полностью определенных таблицах, если М(я) должно быть ограничено разбиением, то М(п) может не быть единственным (см. упражнение 5.7).

Лемма 5.7. Положим, что ли П2 являются двумя системными множествами, определенными на множестве состояний Q автомата А. Тогда если Щ^2, ТО m(jxj)m(n2) и M(ni)

<М(Я2).

Доказательство. Выполните в качестве упражнения.

Важным специальным классом множества пар является пара Mm. Пара множества {щ, nz) является Mm парой тогда и только тогда, когда л;1 = М(л;2) и n2=:m(ni). Задавая первоначальное системное множество я, можно получить пару Mm следующим образом. Вначале вычислим т(я), а затем М(/п (я)), образуя пару множества {М{т{п)), т{п). В то же время можно было вычислить М(л), а затем т(М(я)), получая пару множества (М(л;), т(М(я))). Следующая лемма показывает, что оба эти вычисления приводят в результате к парам Mm.

Лемма 5.8. Если заданы автомат А и системное множество т, определенное на множестве состояний Q из А, то

а) /п(М(т(я))) = т(я),

б) М(т(М(я))) = М(я).

(Так как не возникает опасности в двойственном истолковании результатов, мы будем опускать многократные скобки.)

Рис. 5.9. Таблица состояний и выделение пар для определения М (15, 34, 2).

Доказательство, а) При определении m и М мы получаем следующие выражения:

РКт(я)), (1)

Р(Мт(я), т(я)), (2)

P(Mm(jt), тМт{п)). (3)

Из определения М и выражений (1) и (2) следует, что Mm (я), а на основе леммы 5.7

m (я) < тМт (я). (4)

Аналогично из определения т и выражений (2) и (3) следует, что

тМт (я) < m (я). (5)

Но из выражений (4) и (5) т(я) = тМт(я), и (Mm(я), т(я)) является Mm парой.

б) доказывается аналогично а). Выполните в качестве упражнения-

Следующая лемма показывает, как множество пар Mm может быть использовано для представления всех пар множеств для заданного автомата.

Лемма 5.9. Если задана любая пара множества (я тц), определенная на состояниях автомата А, то существует Mm пара (tj, Тг), такая, что Я1Т5, а ngTj.

Доказательство. Рассмотрим пару множества (т: Тг), где Г1=М(т(я1)), 1:2 = т(я1), которая по лемме 5.8 является Mm парой. Так как Р(я1, Я2), то Я2т(я1) = Т2. Кроме того, Р(я т(я1)) подразумевает, что Я] Мт(я1) =1:,.

Для заданного автомата А с множеством состояний Q разбиение, в котором состояния да и дъ находятся в одном и том же блоке, а все другие состояния находятся в индивидуальных блоках, обозначается как Паь- Если Q содержит п элементов, то

имеются таких разбиений. Системное множество т(яаь)

создается по правилам N{ga,Ik) =К{дъ,1ь), {т{лаь)) для всех Ik. Если А содержит k входных столбцов, то m (паь) будет иметь самое большое k блоков с двумя элементами, а все другие блоки будут содержать один элемент. Таким образом, для каждого Ягз можно сформировать Mm пару (Мт(яг^), т(ягз)). Из этих Mm пар можно получить дополнительно Mm пар на основе следующей леммы.

Лемма 5.10. Для двух системных множеств яь Я2, определенных на множестве состояний, автомата .А, т{л\ -(- Яг) = т(я1)-1--\-т{п2), исключая случай, когда А является не полностью

определенным, а щ, лг и + П2 должны сводиться к разбиениям.

Доказательство. Р{щ,т{щ)) и P(jx2, mCrtg)). Следовательно, исходя из леммы 5.56, Р(я1 + л;2, m (я,)-f т(я,)), и поэтому (на основе определения т)

т (я, -f Л2) < (я,) + т (Я2). (1)

Но так как я, -f- Я2 Я; исходя из леммы 5.7, то т {щ -f Я2) т(я5). Аналогичным образом, m (я]-f Яг) m (лг)- Отсюда

т {щ + Яа) m (лО -+- т {щ)- (2)

Следовательно, из (1) и (2)

т (Л] Л2) = /п ( [) -f- m (Л2).

Лемма 5.10 не является справедливой для не полностью определенных таблиц, если все системные множества сводятся к разбиениям. Рассмотрим таблицу, представленную на рис. 5.10 (такую же, как и на рис. 5.7), и положим П1= (12,3,4), Л2= (13,2,4). Тогда ограничение т(л) должно быть разбиением т(л1) = (14, 2, 3), т(л2)=0; Л1+Я2 = = (123, 4) и т(л1 + лг) = (134, 2) Ф Ф т(п\) --т(л2).

Как следует из леммы 5.10, все суммы т-системных множеств являются также т-системными множествами. Используя все возможные суммы из системных множеств т(лаь) для всех пар состояний qa, qb. Рис. 5.10. Не полностью МОЖНО получить все Mm пары (ль лг), в определенная таблица Которых лг ограничивается тем, что не состояний. должно содержать блоков, имеющих более

двух элементов. Для того чтобы извлечь Mm пар без этого ограничения, полезно представить системное множество л, определенное как совместимое с множествами элементов в том же самом блоке л. Тогда можно определить такое системное множество С(л), что элементы 171, qz, qh находятся в том же самом блоке из С (л) тогда и только тогда,

когда каждая из пар элементов находится в одном и том

же блоке л. Таким образом, если л = (12,23, 13,34), то С(л) = = (123,234). Аналогичным образом, мы определим С~(л) как системное множество, блоки которого содержат не более двух элементов, каждый из которых является таким, что qa = = ь(С'-(л)) тогда и только тогда, когда qa = qb{n). Таким образом, если л = (123, 24, 34), то С-(л) = (12, 13, 24, 34) и С(л) = (123,234). Если л является разбиением, то С(л) = л.