Рис. 4.62. К упражнению 4.10.

4.10. Для каждой из таблиц, приведенных на рис. 4.62, найдите все существенные риски сбоя и rf-трио, а также укажите, в какие переменные состояний в предполагаемых кодированиях состояний должны быть введены

4.7. Найдите однозначное ОВП-кодирование с минимальным числом переменных для каждой из таблиц переходов, показанных на рис. 4.60.

4.8. Для каждой из следующих комбинационных функций получите свободные от риска сбоя реализации суммы произведений и произведения сумм.

а) / [xi, Х2, Хз, Xi) = 22 о- mi, пц, от,5

б) f (xi, Х2, лгз) = X з- 4 mj.

4.9. Для комбинационной функции

/ = (xi, Х2, Хз, Xi) = о- г, Из, mi, mg, me, тг, mi2, mis, m,e. Имеет ли реализация суммы произведений

/ = XiXi + Х1Х3 + XzXi + X2XS

какие-либо риски сбоя при одиночных изменениях входных сигналов? Что означает необходимость свободной от риска сбоя реализации, содержащей все простые импликанты?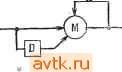

Рис. 4.63. Модели инерционных задержек.

4.12. а) Цепь, показанная на рис. 4.64, а, предлагается в качестве блока задероюек на переменные с тремя состояниями, который гиожет быть использован для* реализации цепей с одиночным элементом задержки для определенных типов кодирования состояния, где М является мажоритарным логическим элементом. Для каких типов кодирования состояний меняет быть использован этот блок задержек?

б) Повторите для цепи, показанной на рис. 4.64,6, г,а.е Bi = СК,- -f- Ctji + + yiVi.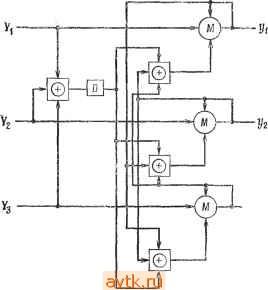

~Уз

элементы задержки для обеспечения необходимого функционирования при одиночных изменениях входных переменных.

4.11. Цепи, представленные на рис. 4.63, предполагаются в качестве моделей инерционных задержек, где М является мажоритарным логическим элементом. Рассмотрите классы входных сигналов, при которых они будут работать.

©J

Рис. 4.64. Реализации блоков задержки на три переменные, упражнение 4.12.

4.13. а) При допущении о том, что параметры не зависят от времени, сократите таблицу переходов, приведенную на рис. 4.65, а.

Ь) Покажите, что таблица на рис. 4.65,6 эквивалентна таблице на рис. 4.65, а при условии, что параметры не зависят от времени.

Рис. 4.65. К упражнению 4.13.

в) Предложите процедуру сокращения таблицы переходов при условии, что параметры не зависят от времени.

4.14. Цепь, показанная на рис. 4.66, б, представляет попытку реализовать таблицу переходов, приведенную на рис. 4.66, а. Определите, существуют ли обстоятельства, при которых конечное поведение цепи не может быть преобразовано в таблицу переходов. Затем опишите их и укажите исправления. Допустите, что только один вход может изменяться одновременно и что имеется достаточно времени между последующими входными изменениями. Будет ли цепь работать правильно, если элемент инерционной задержки заменяется на элемент чистой задерн4ки? (Задержки лннни не ограничиваются по отношению к задержкам логических элементов.)

Х2-1уГ-

Инерционная тка

Рнс 166 к упражнению 4.14.

Рис. 4.67. К упражнению 4.16.

Асинхронные последовательностные цепя 289

4.15. Рассмотрите двухуровневые реализации, соответствующие булевым выражениям

а) xi(xi-\-X2);

б) XiKi + XiXi.

В каждом случае определите, имеются ли какие-либо динамические риски сбоя. Что вы можете сказать о риске сбоя при возможности дистрибутивного выбора?

4.16. Кодирова11ие, показанное на рис. 4.67, является универсальным кодированием с восемью состояниями, использующим 25о = 6 переменных состояния. Покажите, что не требуется перехода, который совершался бы более двух раз. Покажите, как это может быть обобщено на случай 25о переменных состояний, двухкратного перехода при универсальном кодировании состояний для всех So.

Глава 5 СТРУКТУРНО ПРОСТЫЕ РЕАЛИЗАЦИИ ПОСЛЕДОВАТЕЛЬНОСТНЫХ АВТОМАТОВ

5.1. ВВЕДЕНИЕ

Различные реализации одного и того же последовательност-ного автомата, полученные на основе различных методов кодирования, могут очень отличаться по своей сложности. Например, если используются Л-триггеры, то для реализации синхронной таблицы состояний, представленной на рис. 5.1, а и использующей кодирование 2, требуется значительно меньшее число входных логических элементов, чем для реализации, использующей кодирование 1. Первая из реализаций является также

Кодирование 1

Кодирование Z

Рис. 5.1. Две реализации таблицы состояний.

менее сложной в том отношении, что переменные состояний в уравнениях, описывающих следующее состояние, не зависят от некоторых из этих переменных. Будем рассматривать это свойство как уменьшенную зависимость. Кодирование с уменьшенными зависимостями будет, вообще говоря, приводить к структурно простым реализациям последовательностных автоматов.

Поскольку количество отличающихся друг от друга кодирований состояний, использующих минимальное число переменных состояния, возрастает как (2° )!/(log2n)! для автомата с п состояниями [21], имеющиеся методы выбора хорошего кодирования состояний не являются приемлемыми, за исключением очень небольших автоматов. Поэтому мы будем исследовать алгебраические свойства автоматов для того, чтобы эффектив-

НО способствовать получению кодирования состояний, которые будут приводить к реализации с уменьшенной зависимостью. Вначале рассмотрим случай синхронного автомата.

5.2. ПОЛНОСТЬЮ ОПРЕДЕЛЕННЫЕ ОДНОЗНАЧНЫЕ КОДИРОВАНИЯ И АЛГЕБРА РАЗБИЕНИЯ

Разбиение я множества объектов S является такой совокупностью подмножеств Bi, 62, из S (обозначаемое как п = {Ви в2, Bi)), что Bi и Bj = 5 и П 5,- = Ф, если i ф \, где Ф является пустым множеством.

Для того чтобы исследовать алгебраические свойства последовательностных автоматов, полезно рассмотреть переменные состояний при кодировании состояний и их отношение к теории разбиения. При полностью определенном однозначном кодировании состояний для автомата А каждая переменная состояний определяет два блока разбиения Хуг на множестве состояний А при котором каждое состояние, имеющее уг = 0, находится в одном блоке, а каждое состояние, имеющее = принадлежит другому блоку.

При кодировании состояний, показанном на рис. 5.1,б,Ту, = = (1234,56), Tj = (1256,34), Tj == (135,246), где различные блоки разбиения разделяются запятыми, а состояния в блоке группируются вместе без каких-либо разделяющих символов.

Разбиение, в котором каждый блок имеет один член из 5, является 0-разбиением. Разбиение, в котором все члены из S находятся в одном блоке, является 1-разбиением. 0-разбиение и 1-разбиение будут рассматриваться как тривиальное разбиение. Все другие разбиения являются нетривиальными.

Пример 5.1. Положим, 5 = {1, 2, 3, 4, 5}; (12,345) является нетривиальным разбиением; (1,2,3,4, 5) является 0-разбиением; (12345) является 1-разбиением; (12,34) не является разбиением S, так как S не находится в каком-либо блоке разбиения; (12, 123,45) не является разбиением 5, так как 1 и 2 находятся более чем .в одном блоке.

Для разбиения эх, определенного на множестве 5, если два элемента Qi, qj находятся в одном и том же блоке п, будем обозначать это как qi = q/ (п). Аналогично, если множество А элементов содержится в некотором блоке л, будем обозначать это посредством Л (эх). Для двух разбиений щ, зхг эХ] ==3X2 тогда и только тогда, когда каждый блок из щ является идентичным

) Поскольку большинство результатов -получено -применительно к. разбиениям, которые определены на других наборах, мы будем использовать обобщенный символ S, понимая под этим, что S = Q для разбиений,: .определенных на состояниях автомата. .

(1,23)

(123)

(12,3)

(13,2)

блоку ИЗ щ И наоборот. Для двух разбиений Я], Яг, определенных на одном и том же множестве S, щ П2 тогда и только тогда, когда каждый блок из щ содержится в блоке из (будем говорить, что является большим, чем щ, а щ является меньшим, чем Лг, если Лущ и зх, ф П2). Это отношение определяет частичное упорядочение разбиений, определенных на множестве S. Такое частичное упорядочение может быть изображено в виде решетчатой структуры, как показано на рис. 5.2 для S = {1,2,3}. Произведение двух разбиений

является наибольшим разбиением, меньшим или равным каждому из них. Формально произведение щ и щ, обозначаемое как щ щ, является разбиением, таким, что

а) щ П2щ,

б) Я] Яг Яг,

в) если для любого другого раз-(1,2,3 биения

Рис. 5.2. Решетка разбиений. щ И я Яг, ТО я Я1 Яг.

Произведение нескольких разбиений Ti, Тг, т„ обозна-

чается Г1 и равняется ((((tj Тг) Тз) ...) т„). Легко видеть, t=i

что операция умножения является коммутативной и ассоциативной

Лемма 5.1. Если щ и Яг являются двумя разбиениями, определенными на множестве S, а и Qj являются двумя элементами из S, то Qi - Qj (Я1 Яг) тогда и только тогда, когда qt = = 9/Ы и 9г = 9/(я2).

Доказательство. Необходимость. Предположим, что qi = = 9у(Я1-Я2), но qi¥qi{ni) (или qtФq]{щ)) Тогда Я1-ЯгЯ1 (или Я1-Я2Я2), что противоречит определению Я] Яг.

Достаточность. Предположим, что qi = qj (Я]) и qi=q] (яг), но qj ф q/ini Яг). Тогда определим я следующим образом: все состояния в блоках Я: Яг, содержащих qi или q], комбинируются в один блок из я; все другие блоки из я являются идентичными блоками Я] Яг. Тогда если Я1-Яг<Я1, Яг, то яЯ] и яЯг (выполните в качестве упражнения), а я> > Я] Яг. Это противоречит определению щ щ, и, следовательно, лемма доказана.

Как следствие из леммы 5.1 произведение Я] и Яг может быть выполнено посредством взятия пересечения каждого блока из Я] с каждым блоком из Яг. Например, если Я1 = {12, 345} и П2 = {124,35}, то Я1 Яг = {12,35,4).

Дху. =0. В случае, если Д О, то имеются два таких

i = l

состояния qi и qj, что

И, следовательно, qi и qj имеют один и тот же код в г/ г/2, , п, то является некорректным кодированием состояний.

Задавая разбиение п, определенное на множестве состояний Q автоматом М, положим, что 5; = {j, г^, , 9; .} является блоком из л. Тогда

является множеством содержимого следующих состояний из всех состояний в Bi для входа . Упорядоченная пара разбиений (зХ], ЗХ2) определенная на множестве состояний Q, является упорядоченной парой для М, обозначаемой Р {щ, 3X2), тогда и только тогда, когда для каждого блока Bj из зх и каждого входа Ik существует блок Bi из 3x2, такой, что N (Bi, Ik) В/-Если ЗХ] = ЗХ2 (т. е. Р (3x1,3x2)), то 3Xi обладает свойством подстановки (СП), обозначаемым как S (я,).

Пример 5.2. Для таблицы, представленной на рис. 5.3, Q = = {1,2,3,4}. Рассмотрим разбиения (13,2,4) и (14,23). /V(13,0)=23, а iV(13, 1)=14. Следовательно, Р[13,2,4), (14,23)], т.е. (13,2,4) и (14,23) образуют пару разбиения. Аналогично положим (12,34) = (Bi,B2). iV(Bi,0) = В2; iV(Bi, 1) = = Bi; iV(B2,0)=2crBi; Л/(В2, 1)=B2. Следовательно, 5(12,34); т.е. разбиение (12,34) обладает свойством подстановки.

Следующие лемма и теорема связывают методику пар разбиения с однозначным кодированием состояний, имеющим уменьшенную зависимость.

Лемма 5.2. При заданном корректном однозначном кодировании состояний с переменными г/i, г/2, , Уп на состояниях Q из таблицы состояний М Уц, (значение следующего состояния Уи) является независимым от yj (и допущении, что задержки реализуются на D-триггерах в качестве элементов памяти).

) За исключением случаев, где имеет место явное определение ситуаций, мы предполагаем, что всюду в этой главе задержки на D-триггерах используются в качестве элементов памяти.

Корректное однозначное кодирование состояний с переменными г/ У2, , Уп на множестве состояний Q генерирует множество из двух блоков разбиения Ху, Ху, Ху, таких, что

Рис. 5.3. Таблица состояний из Рис. 5.4. Таблица состояний и кодиро-примера 5.2. вание с уменьшенной зависимостью.

Теорема 5.1. Для заданной таблицы состояний М при однозначном кодировании состояний на множестве переменных А = == {Уи У2, , Ук] и реализации М, использующей кодирование состояний, переменная состояний Yi зависит от соответствующего подмножества Aj из А тогда и только тогда, когда

Р( Л. у т^йЛ , 3 Yi зависит только от у, тогда и только тог-

да, когда Р{ху., Ту.) (т. е. 5(ту.)).

Доказательство. Непосредственно следует из леммы 5.2.

Пример 5.3. Таблица состояний, кодирование состояний и разбиение Ту 5(ту,), показаны на рис. 5.4. Следовательно, Y\ зависит только от у и как это предсказывается теоремой 5.1. Значение следующего состояния j/i задается посредством Y\ - = xyi + xyi.

соответствующая цепь возбуждения является независимой от i/j), тогда и только тогда, когда Р Ху., ty.

Доказательство. Необходимость. Предположим, что является независимым от у/ и выражение .П.ч^г/;, не

является истинным. Тогда должны существовать два состояния Qi и Qp и вход /т, такие, что qi = qp{tyi) для всех ij и N (Qi, Ifn) ф N {qj, Im) (т^г^). Но тогда Y не может быть независимым от У1, что является противоречием.

Достаточность. Предположим, что Р П Ту., Tj,j,j. Тогда

для любых двух состояний qi и qj, таких, что qi - qj{y, для всех имеет место N {q, 1) = {qj, / ) {у^)- Следовательно, Yk может быть определено из входов и переменных yi, 1ф].