Уо являются

Fl == %2 + г/1 (Ш, Тг = ху1 + у2 {хух).

На рис. 4.52 показана реализация этих уравнений без введенных элементов задержки. Заметим, что мы должны использовать логический элемент ИЛИ для реализации Z\ и логический элемент НЕ-И для реализации Z2 в отличие от обшей

x X

>

Рис. 4.52. Реализация цепей без элементов задержки, использующая специальные схемы.

формы, показанной на рис. 4.50. Это упрощение стало возможным потому, что как Zi, так и Z2 содержит только один терм и нет необходимости в явном дополнении входных переменных.

4.9. ЛОГИЧЕСКИЕ ЭЛЕМЕНТЫ

С НЕОГРАНИЧЕННЫМИ ЗАДЕРЛКАМИ

Различные модели асинхронных цепей были предложены Мюллером и Бартки [17]. Предполагается, что в ветвях цепи отсутствуют паразитные задержки, а границы значений паразитных задержек, связанных с логическими элементами, неизвестны, хотя и считается, что они положительны и конечны. Эти допущения оказываются полезными при исследовании поведения цепей, в которых задержки логических элементов могут изменяться в неограниченно широком диапазоне. Цепи, поведение которых не зависит от значений паразитных задержек, называются независимыми от скорости цепями.

При допущении об отсутствии ограничений на время задержки, вызываемой логическими элементами, невозможно определить требуемый при основном режиме функционирования интервал между последующими изменениями входных переменных. Следовательно, необходимо, чтобы сама цепь генерировала сигнал для указания своей готовности к получению следующего входного сигнала. Было предложено несколько способов проектирования цепей, которые генерируют такие сигналы готовности

(завершения), для того чтобы функционировать в условиях указанной неопределенности задержки, вносимой логическими элементами [2, 8, 16]. Ниже в общих чертах будет изложен один из этих методов [2].

Детектор завершения

Цепи с сигналами завершения

На рис. 4.53 показана общая модель цепей с сигналами завершения. Подсхема, названная логической цепью, может реализовать комбинационную или последовательностную функцию. Детектор завершения генерирует сигнал завершения, когда выходы логической цепи достигли устойчивого состояния. Входы и выходы кодируются таким образом, чтобы устойчивые состояния могли быть определены детектором завершения. Получая

сигнал завершения, источник генерирует на входе следующий код, поступающий в логическую цепь. Необходимость связи между входом логической цепи и детектором завершения будет объяснена ниже.

Одним из кодов, которые могут быть использованы в цепях, генерирующих сигналы завершения, является автосинхронный код. В этом коде каждая двоичная входная или выходная переменная представляется двумя переменными, которые должны указывать друг другу о завершении. А именно ЛГ] = О представлется как Хп = О, Хю = 1, а xi = I представляется как лгц = 1, лгю = 0. Переходы между двумя кодовыми словами всегда совершаются через промежуточное нулевое состояние, в котором все переменные состояния обращаются в 0. Например, две переменные хи х^, которые изменяются от 01 до 10, должны быть представлены четырьмя переменными лгц, лгю, Xz\, Хго, подвергающимися переходам

Рис. 4.53. Цепь с сигналами завер шения

ОНО-> 0000-

1001.

Логическая цепь должна быть спроектирована таким образом, чтобы она выдавала выходное кодовое слово только тогда, когда получается входное кодовое слово. Выход из промежуточного нулевого состояния может произойти единовременно либо по мере изменения переменных состояний. Переход в промежуточное нулевое состояние определяется по наличию всех нулей на входах и выходах. Цикл работы цепи должен быть следующим: источник посылает кодовое слово в цепь, которая генерирует соответствующее выходное кодовое слово. Проверяя этот выход, детектор завершения генерирует сигнал завершения, который заставляет источник генерировать

о 10 1 0 1

0 1 1 о I о

1 о О 1 10 1 0 10 0 1

Рис. 4.54. Таблица истинности для функции у = xi@ Х2, закодированной

в автосинхронном коде.

хронного кода, получаем частичную таблицу истинности, представленную на рис. 4.54. Так как хц и Хго не могут быть оба одновременно равны 1 при i = 1, 2, то можно обрабатывать такие входные комбинации без особых забот. Другие комбинации могут быть пройдены в процессе переходов, и как уи так

Рис. 4.55. Карты Карнау для автосинхронных функций.

И уо присваивается значение О, как показано на картах Карнау, приведенных на рис. 4.55. Таким образом, цепь будет выдавать на выходе кодовое слово только после того, как входы завершат свой переход к кодовому слову. Две выходные функции могут быть реализованы в следующей двухуровневой форме суммы произведения:

У1 -ХцХ^о + Х10Х21,

Уй-ХцХгх -\-ХюЛГго-

Реализация этих функций и детектора завершения показана на рис. 4.56. Детектор завершения имеет два выхода, помеченных S и С. Значение S = 1 указывает, что было установлено

нулевое состояние. Цепь реагирует на вход в промежуточное нулевое состояние, вырабатывая сигнал выхода этого состояния. После этого детектор завершения генерирует отличный от других сигнал завершения, по получении которого источник выдает следующее кодовое слово.

Пример 4.25. Допустим, что реализуемая функция должна быть у = Х2. Кодируя вход и выход с помощью автосин-

нулевое состояние, что в свою очередь послужило причиной выдачи источником следующего кодового слова. Аналогичным образом, значение С = 1 указывает, что было определено кодовое слово, что заставляет источник генерировать сигнал перехода в нулевое состояние. Заметим, что детектор, сигнализирующий о переходе в нулевое состояние, присоединяется к выходам логической цепи, так же как к ее выходам, что обсуждалось ранее. Если детектор присоединяется только к выходам

Рис. 4.56. Реализация автосинхрониых функций и детектора завершения.

цепи, то может быть выработан преждевременный сигнал завершения, который, в свою очередь может послужить причиной того, что источник изменит свое состояние до того, как цепь завершит свою реакцию на предшествующий переход.

Если с помощью этого метода реализуется функция с многими выходами, то детектор выходного кодового слова необходимо модифицировать, связывая каждую пару выходов с логическим элементом ИЛИ и соединяя все выходы элементов ИЛИ со схемой И. Вместо автосинхронного кода для кодирования входов и выходов могут быть использованы коды т/п {т изп), где т переменных из полного числа п переменных являются 1 для любого кодового слова.

Этот метод может быть также модифицирован для реализации последовательностных цепей при допущениях об отсутствии определенных границ для величины времени запаздывания логических элементов. Как и в случае комбинационных цепей, предполагается, что требуются входы и выходы, отличающиеся для кодовых слов (автосинхронных или т/п) и для промежу-

точных нулевых состояний. Если последовательностная цепь идентифицируется с помощью таблицы переходов, то мы дополняем эту таблицу введением столбца промежуточного нулевого состояния (как и в случае реализации цепей с многократным изменением входов, который обсуждался ранее). Столбец промежуточного нулевого состояния содержит только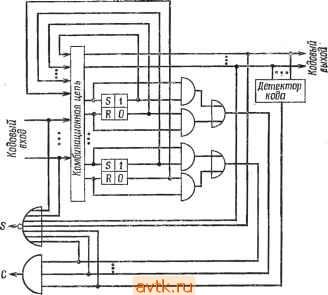

Рис 4.57. Реализация последовательностной цепи, использующая сигнал завершения.

устойчивые состояния, но теперь определение выходов в столбце промежуточного нулевого состояния производится таким образом, чтобы выход из него не зависел от состояний. Все переходы состояний происходят тогда, когда состояния входов изменяются от положений, соответствующих промежуточному нулевому состоянию, к положению, соответствующему надлежащему кодовому слову.

На рис. 4.57 показан этот метод реализации последовательностной функции. Для каждой переменной состояния используется триггер. Когда в цепи имеет место переход в промежуточное нулевое состояние, все триггеры функций возбуждения находятся в нулевом состоянии. Если входом является кодовое слово, все триггеры цепи, реализующей функцию возбуждения, находятся в состоянии О независимо от того, находились ли они уже в желаемых состояниях или нет. В этой схеме каждый триггер должен быть в таком состоянии, в котором он возбуж-

дается, когда цепь завершает реакцию на переход от промежуточного нулевого состояния к кодовому слову. В дополнение к этому выходы цепи должны быть кодовыми словами. Реакция на переход от кодового слова к промежуточному нулевому состоянию завершается, когда входы, выходы и состояние триггеров цепи возбуждения все являются нулями.

Кодирование состояний для этого типа реализации должно быть ОВП-кодированием, один из вариантов которого был предложен Лю. Этот вид кодирования обладает тем свойством, что все неустойчивые состояния приводят к одному и тому же устойчивому состоянию в любом столбце и само устойчивое состояние выделяется из всех других состояний в этом столбце за счет подмножества переменных состояния. В результате триггерные функции возбуждения могут быть реализованы в виде суммы произведений таким образом, что не более чем одна импликанта функции изменяется к 1 в течение любого перехода, предотвращая тем самым преждевременную генерацию сигналов завершения. Если две или более импликанты функции переходят в 1 в течение перехода, то вырабатывается сигнал завершения после того, как первая из них перейдет в 1, и прежде чем цепь завершит реакцию на входной переход. Это может привести к тому, что источник изменит свои выходы прежде, чем цепь придет в устойчивое состояние, что в свою очередь приведет к неправильному ее функционированию.

При проектировании сложных схем удобно строить их путем соединения модулей, реализующих простейшие функции. Такие соединения модулей допустимы между модулями, генерирующими сигналы завершения. Если выходы модуля А соединяются с модулем В, то сигналы завершения, генерируемые модулем б, возвращаются по цепи обратной связи к модулю А. Модули должны быть спроектированы таким образом, чтобы выходы модуля А не изменялись до тех пор, пока модуль В не завершит реакцию на предшествующий выход А. Это может быть достигнуто путем соединения элементов памяти (таких, как триггеры) с выходами. Обсуждавшийся выше основной подход к проектированию комбинационных и последовательностных цепей может быть модифицирован для того, чтобы обеспечить запоминание на выходе в пределах каждого модуля. Более сложные схемы могут быть реализованы за счет соединений спроектированных таким способом модулей как для комбинационных, так и для последовательностных цепей.

БИБЛИОГРАФИЯ И КОММЕНТАРИИ

Модель асинхронных последовательностных автоматов и цепей и использование таблиц переходов предложены Хаффма-ном [10], который также получил универсальное 2So- 1. коди-

ЛИТЕРАТУРА

1. Armstrong D. В., Friedman А. D., Мепоп Р. R., Realization of Asynchronous Sequential Circuits Without Inserted Delay Elements, IEEE Trans. Computer, vol. C-17, pp. 129-134, February 1968.

2. Armstrong D. В., Friedman A. D., Menon P. R., Design of Asynchronous Circuits Assuming Unbounded Gate Delays, IEEE Trans. Computers vol C-18, pp. 1110-1120, December 1969.

3. Breuer M. A., Harrison R. L., Procedures for Eliminating Static and Dynamic Hazards in Test Generation, IEEE Trans. Computers, vol. C-23 pp. 1069-1078, October 1974.

4. Eichelberger E. В., Hazard Detection in Combinational and Sequential Switching Circuits, Proc. Fifth Annual Symposium on Switching Circuit Theory and Logical Design, pp. 111-120, 1964, Also IBM J. of Res. & Dev., pp. 90-99, 1965.

5. Fantauzzi G., An Algebraic Model for the Analysis of Circuits, IEEE Trans. Computers, vol. C-23, pp. 576-581, June 1974.

рование состояний [И]. Условия основного режима функционирования были формально определены Мак-Класки [15]. Проблема сокращения таблицы состояний для синхронных автоматов рассматривалась Паулем и Ангером [18], а для асинхронных автоматов Ангером [23]. Универсальное кодирование с помощью множества разделяемых строк для 8 и 12 состояний было предложено Саусером [19]. Кашеф и Макхи [12] разработали относительный класс кодирования, называемый кодами с дополнительной проверкой на четность. Универсальное ОВП-кодирование состояний предложено Хэммингом [9]. Лю [13] и Трэйси [21] разработали процедуры для получения однозначного ОВП-кодирования, а Фридман, Грэхэм и Ульман [6] указали на границы универсальных ОВП-кодирований, а также рассмотрели многозначные ОВП-кодирования. Влияние риска сбоев, их предотвращение и определение были рассмотрены Ангером [22] и Айшельбергером [4]. Девятизначная алгебра для определения динамических рисков сбоя была разработана Фантоци [5]. Аналогичная, но менее формализованная процедура была предложена Бреуром и Гаррисоном [3].

Реализация цепей с одновременным изменением входных цепей была выполнена Фридманом и Меноном [7], а учет неограниченных изменений входных сигналов был выполнен Ангером [24]. Армстронг, Фридман и Менон [2] рассматривали модель, в которой задержки линии были меньше, чем задержки логических элементов, а также модель линии с неограниченной задержкой. Модель задержки, не имеющей ограничений, была разработана Мюллером и Бартки [17]. Методы конструирования были разработаны Миллером [16] и Хэммелом [8]. Использование авгосинхронных кодов при проектировании асинхронных цепей было впервые предложено Симсом и Греем [20].

УПРАЖНЕНИЯ

4.1. Рассмотрите таблицу переходов, представленную на рис. 4.58. Содержимое N (2,01) обозначено как А. Охарактеризуйте таблицу как таблицу с однократным изменением выхода, с многократным изменением выхода, нормального режима, основного режима и т. д., если а) А - I, б) А - 2, в) Л == 3, г) Л = 4.

6. Friedman А. D., Graham R. L., Ulman J. D., Universal Single Transition Time Asynchronous State Assignments, IEEE Trans. Computers, vol C-18 pp 541-547, June 1969.

7. Friedman A. D., Menon P. R., Synthesis of Asynchronous Sequential Circuits with Multiple-Input Changes, IEEE Trans. Computers, vol. C-17, pp. 559-566, June 1968.

8. Hummel D., Ideas on Asynchronous Freedback Networks, Proc. Fifth Annual Symposium on Switcliing Circuit Theory and Logical Design, pp. 4- II, 1964.

9. Hamming R. W., Error Detecting and Correcting Codes, BSTJ, vol. 29, pp. 147-160, April 1950.

10. Huffman D. A., The Synthesis of Sequential Switching Circuits, 1. Franklin Inst, vol. 257, pp. 161-190, March 1954, pp. 275-303, April 1954.

11. Huffman D. A., A Study of Memory Requirements of Sequential Switching Circuits, Technical Report № 293, Research Laboratory of Electronics, MIT, Cambridge, Mass., 1955.

12. Kashef R. S., McGhee R. В., Augmented Parity Check Codes for Encoding of Asynchronous Sequential Machines, IEEE Trans. Computers, vol. C-22, pp. 891-896, October 1973.

13. Liu C. N., A State Variable Assignment Procedure for Asynchronous Sequential Switching Circuits, 1. ACM, vol. 10, pp. 209-215, April 1963.

14. Mago G., Realization Methods for Asynchronous Sequential Circuits. IEEE Trans. Computers, vol. C-20, pp. 290-297, March 1971.

15. McCluskey E. J., Fundamental Mode and Pulse Mode Sequential Circuits, Proc. IFIP Congress, Munich, Germany, North Amsterdam Publishing Company, Amsterdam, pp. 725-730, 1962.

16. Miller R. E., Switching Theory, vol. 2, Wiley, New York, 1965.

17. Muller D. E., Bartky W. S., A Theory of Asynchronous Circuits, Proc, of an International Symp. on the Theory of Switching, vol. 29, Annals of the Computation Laboratory of Harvard Univ., Harvard Univ. Press, pp. 204-243, 1959.

18. Paull M. C, Unger S. H., Minimizing the Number of States in Incompletely Specified Sequential Switching Functions, IRE Trans. Elec. Computers, vol. EC-8, pp. 356-367, September 1959.

19. Saucier G., Ecodings for Asynchronous Sequential Networks, IEEE Trans. Elec. Computers, vol. EC-16, pp. 365-369. June 1967.

20. Sims J. C, Gray H. J., Design Criteria for Autosynchronous Circuits, Proc. Eastern Joint Сотр. Conf., pp. 94-99, December 1958.

21. Tracey J. H., Internal State Assignments for Asynchronous Sequential Machines, IEEE Trans. Elec. Computers, vol. EC-15, pp. 551-560, August 1966.

22. Unger S. H., Hazards and Delays in Asynchronous Sequential Switching Circuits, IRE. Trans. Circuit Tlieory, vol. CT-6, pp. 12-25, March 1959.

23. Unger S. H., Asynchronous Sequential Circuits, Wiey Interscience, New York, 1969.

24. Unger S. H., Asynchronous Sequential Switching Circuits with Unrestricted Input Changes, IEEE Trans. Computers, vol. C-20, pp. 1437-1444, December 1971.

Рис. 4.58. К упражнению 4.1.

б) цепь, в которой начиная с устойчивого состояния 1 при Xi - Х2 = О и Z - О изменение значения выхода происходит только тогда, когда значения !Ci изменяются последовательно 3 раза или значения изменяются последовательно 2 раза. Затем сократите примитивную таблицу таким образом, чтобы минимизировать количество состояний.

4.3. Рассмотрите булево выражение

/ = {XiXz + XjXs) (Xl {Xi + Xs) + XlXsXtXs)

и соответствующую комбинационную цепь.

а) Имеет ли цепь какие-либо статические риски сбоя при однократных изменениях переменных?

Рнс. 4.59. К упран^пению 4.3.

б) Имеет ли цепь какие-либо динамические риски сбоя?

в) Найдите свободную от риска сбоя реализацию суммы произведений для функции, представленной на рис. 4.59.

4.4. Для Канадой из таблиц состояний, представленных на рис. 4.60, определите, если возможно, однозначное кодирование состояний, в котором

4.2. Сконструируйте примитивную таблицу переходов для асинхронной цепи, которая функционирует как:

а) цепь, которая имеет два двоичных входа лг] и jc2 и один двоичный выход z, причем во время любого перехода может изменяться только одна входная переменная;

каждый переход требует только одного изменения переменной состояния при допущении однократного изменения входной переменной.

Рис. 4.60. К упражнениям 4.4 и 4.7.

4.5. Используя кодирование переменных состояния, указанное на рис. 4.14, для таблицы переходов, приведенной на рис. 4.13, определите У-матрицу.

4.6. Для таблиц переходов, представленных на рис. 4.61, найдите

Рис. 4.61. К упражнению 4.6.

а) кодирование состояний с минимальным числом переменных, используя множество связанных строк,

б) кодирование состояний с минимальным числом переменных, используя множество разделяемых строк.