X, X

Рис. 4.9. Сокращение таблицы переходов с параметрами, зависящими от

времени.

Расширенная таблица может быть сокращена и сведена к таблице переходов, показанной на рис. 4.9,6, которая эквивалентна таблице на рис. 4.9, а при условии зависимости параметров от времени. Допущение, что длительность конкретного состояния выхода пропорциональна количеству последовательных внутренних состояний, в течение которых получаются выходы, может быть проверено исходя из того, что, когда имеют место многократные изменения выходов, относительные величины продолжительности изменений для этих обеих таблиц переходов также являются одинаковыми.

Заметим, что переходное состояние 2 из таблицы на рис. 4.9, а заменяется состояниями 6, 7 и 8, а само состояние 2 может быть исключено и, следовательно, не перекрывается каким-либо состоянием в сокращенной таблице.

Если делается предположение, что параметры не зависят от времени, то определение совместимости должно быть модифицировано таким образом, чтобы не учитывались длительность и моменты получения выходных состояний. Например, последовательности 010, 00110 и 0001000 должны рассматриваться как существенно эквивалентные. Говорят, что два состояния и q, являются В-совместимыми, если для каждого входа выходная последовательность, генерируемая автоматом в состоянии qt, является существенно эквивалентной выходной последовательности, генерируемой автоматом в состоянии qj (или может быть сделана существенно эквивалентной с помощью введения надлежащим образом выбранных определений не определенных состояний выходов), а устойчивые состояния, достигаемые в обоих случаях, также являются В-совместимыми. Процедура сокращения таблицы переходов МИВ при допущении, что параметры не зависят от времени, состоит из расширения таблицы, как это выполняется в случае зависимости ее параметров от времени, и использовании В-совместимости для сокращения расширенной таблицы. Однако эта процедура не всегда может привести к минимальному решению при интерпретации независимости параметров от времени (см. упражнение 4.13).

Пример 4.4. В расширенной таблице переходов, показанной на рис. 4.9, б, состояния 1 и 6 являются В-совместимыми в дополнение к состояниям, которые были найдены как совместимые в примере 4.3. Хотя они имеют различное следующее состояние в столбце 01, оба они достигают одного и того же устойчивого состояния, обозначенного 3, при котором вырабатывается выходная последовательность 10. Поскольку для обоих состояний конечное состояние является одним и тем же, множество состояний не подразумевается. Следовательно, таблица переходов.

Приведенная на рис. 4.9, а, может быть сокращена до таблицы с тремя устойчивыми состояниями (рис. 4.10) при условии, что параметры не зависят от времени.

x, .V,

Рис. 4.10. Сокращенная таблица переходов с параметрами, не зависящими

от времейи.

4.4. КОДИРОВАНИЕ СОСТОЯНИЙ

На рис. 4.11 показана общая модель асинхронных последовательностных цепей [10], которая в дальнейшем будет использоваться в большинстве рассуждений, приводимых в этой главе. Модель аналогична модели для синхронных цепей, за исключением того, что здесь отсутствуют тактовые сигналы. В синхронных цепях тактируемые D-триггеры могут быть моделированы элементами задержки. В асинхронных цепях элементы задержки могут быть использованы в контурах обратной связи, но нельзя сделать допущения о том, что величины задержек одинаковы. Внутреннее состояние цепи представляется переменными состояния Уи а значения переменных следующего состояния обозначаются через У г= 1, 2, п. Переменные Хи Хт И Zu Zu представляют соответственно вход и выход цепи.

Первый шаг при проектировании асинхронной последовательности цепи, реализующей заданную таблицу переходов, состоит в том, чтобы представить внутренние состояния в виде комбинаций значений двоичных переменных состояний. Эт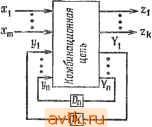

Рис. 4.11. Модель асинхронных последовательностных цепей.

) Заметим, что значения выходов опущены в таблице переходов. В остальной части главы значения выходов будут опускаться из таблиц переходов всюду, где интересующие нас проблемы касаются только поведения состояний. Мы будем предполагать, что такие таблицы переходов являются сокращец-цьши.

процедура является так называемой задачей присваивания кодов или просто кодированием асинхронных состояний и отличается от аналогичной процедуры для синхронных цепей в нескольких аспектах.

Для синхронного автомата необходимое количество переменных состояния равно riog2 nl = So и достаточно для представления п состояний, а кодирование может быть сделано произвольным образом без учета воздействия соответствующей операции, пока не будет закодировано более чем одно состояние, хотя структурная сложность реализации будет зависить от того, как проведено кодирование. Для асинхронной таблицы переходов должны быть удовлетворены дополнительные ограничения и So переменных состояния уже не является достаточным.

Рассмотрим таблицу переходов'), кодирование состояний А, а также их реализацию, показанную на рис. 4.12. Допустим, что цепь была устойчива в состоянии 2 (представленном yi = О, 2=1) при входном сигнале х=1. При переходе из этого состояния, когда X изменяет значение выхода от 1 до О, логический элемент G2 начнет переходить в состояние 1, а обе переменные Yi и Уг начнут изменять свои значения. Если у2 перейдет в состояние О прежде, чем yi перейдет в состояние 1, то логический элемент G2 начнет переходить в состояние О, а пере- менная г/i может колебаться или даже стать устойчивой при У1 =0 вместо f/i = 1, если связанная с G4 задержка оказывается достаточно большой. Аналогичные процессы происходят и в том случае, когда сначала изменяется yi. В результате подобных изменений цепь может проходить через состояние 1, представленное у1 = у2~ О, если сначала изменяется г/г, или через состояние 4, представленное yi= у2-\, если сначала изменяется У\.

Однако оба эти состояния приводят к состоянию 1 в столбце О таблицы переходов, а не к правильному следующему состоянию 3, которое было бы достигнуто, если бы у\ и г/2 изменялись одновременно. Таким образом, достигаемое окончательное состояние будет зависеть от относительных величин имеющихся в цепи побочных задержек. На практике устойчивое состояние может быть неопределенным или цепь может колебаться, что обусловлено изложенными выше факторами. Подобное затруднение не встречается в синхронных цепях, поскольку тактовый импульс не дает возможности изменяться переменным состояния, которые использовались при выработке возбуждений,

до тех пор, пока они не станут устойчивыми, эффективно гарантируя тем самым, что их изменение произойдет одновременно.

Когда две или более переменных изменяются в течение перехода, то говорят, что имеет место состязание между изменяющимися переменными. В таблице, приведенной на рис. 4.12,

Кодиртше А

Кедирвтие В

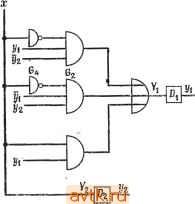Рис. 4.12. Таблица переходов и кодирование состояний (в); реализация таблицы переходов (б).

переменные состояния t/i и при кодировании А вовлекаются в состязание при переходе от состояния 2 к состоянию 3, а также при переходе от состояния 4 к состоянию 1. Если достигаемое окончательное состояние зависит от порядка изменений, как в этом случае, то говорят, что состязание является критическим. В противном случае оно является некритическим.

При кодировании В для той же таблицы переходов все переходы между состояниями отличаются точно на одно состояние

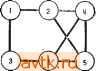а б

Рис. 4.13. Таблица переходов (а); граф переходов для этой таблицы (б).

каждому СОСТОЯНИЮ присвивался только один код. Такое при-свивание кода называется однозначным кодированием. Однако не всегда возможно однозначное кодирование так, чтобы все переходы происходили между смежными кодами состояний.

Рассмотрим таблицу переходов, представленную на рис. 4.13, а.

Ненаправленный граф, показанный на рис. 4.13,6, имеет узлы, соответствующие состояниям таблицы переходов. Он имеет ребро между двумя узлами тогда и только тогда, когда имеется непосредственный переход между двумя состояниями. Этот граф, который мы будем называть графом смежности таблицы переходов, показывает состояния, коды которых должны быть смежными. Из рассмотрения графа смежности видно, что коды состояний 2, 4 и 5 должны быть смежными между собой, как и коды состояний 4, 5 и 6, для того, чтобы осуществились все переходы состояний при изменении только одной переменной состоящая. Однако иметь три таких двоичных кода, в которых

переменных (смежные состояния). Такое кодирование свободно от состязаний и, следовательно, подходит для асинхронной таблицы переходов. Свободное от состязаний кодирование является достаточным, но не необходимым условием для должного функционирования цепи, как это будет показано позже.

Комбинация значений состояния переменных, используемая для представления состояния цепи, называется кодом состояния. При рассмотренных до сих пор присваиваниях кода

каждая пара этих кодов отличалась бы точно на 1 бит, невозможно. Отсюда следует, что для таблицы переходов, представленной на рис. 4.13, а, не существует такого однозначного кодирования состояния, при котором все переходы осуществлялись бы между смежными состояниями.

Для преодоления трудности, с которой мы встретились в вы-щеприведенном примере, могут применяться различные методы. В одном из таких методов разрешаются переходы между несмежными состояниями. В том случае, когда в течение перехода должны изменяться две или более переменных состояния, они могут изменяться либо одновременно, если не создают критического состязания, либо в некотором заранее предписанном порядке. В другом методе используется больше одного элемента кода на состояние. В этом случае можно получить такое кодирование состояний, чтобы переходы к другим состояниям происходили только между смежными состояниями. Более эффективные многозначные кодирования (использующие более одного кода на состояние) могут быть получены, если допускаются некритические состязания.

4.4.1. КОДИРОВАНИЕ С ПОМОЩЬЮ МНОЖЕСТВА СВЯЗАННЫХ СТРОК

Один из методов получения такого кодирования, при котором любой переход может быть сделан с помощью последовательности изменений одной переменной, состоит в том, что присваивается множество кодов /?, каждой строке (состоянию) qi таблицы переходов. Множество кодов (точек), присвоенных строке таблицы переходов, называется множеством строк. Если любой член множества строк может быть получен из любого другого члена того же самого множества с помощью последовательности изменений одной переменной без прохода через какую-либо точку, которая не принадлежит этому множеству, то множество кодов называется множеством связанных строк. Говорят, что два множества связанных строк Ri и Rj должны быть межконтурными, если имеется некоторый код в Ri, который является смежным с некоторым кодом в Rj. Для того чтобы использовать кодирование с помощью множества связанных строк применительно к таблице переходов, множества строк, присвае-мые состояниям, между которыми имеются переходы, должны быть межконтурными. Допустим, что Ri и Rj являются межконтурным множеством строк, присваиваемых состояниям qi и qj соответственно. Переход от qi к qj осуществляется вначале выполнением последовательности переходов внутри Ri до тех пор, пока не будет достигнута точка, смежная с некоторой точкой в Rj, а затем выполняется переход к точке в Rj. Межконтурный

Рис. 4.14. Кодирование состояний с помощью множества связанных строк.

совершаться к коду 1011 (другому коду для состояния 6) посредством изменения г/4. Затем будет изменяться уз к О для того, чтобы достигнуть состояния 4, представленного кодом 1001. Теперь если входные сигналы изменяются на 01, то достигается состояние 5, представленное кодом 1111, через код 1101, который входит в множество строк, присваиваемых состоянию 4. Этот переход показан пунктирными стрелками на рис. 4.14.

При кодировании, показанном на рис. 4.14, любой переход к новому состоянию в таблице переходов, представленной на рис. 4.13, может быть сделан самое большее за два шага. Максимальное число шагов, требуемое для перехода к любому состоянию при использовании конкретного кодирования состояния, рассматривается как время перехода при кодировании. Таким образом, кодирование состояний из примера 4.5 имеет время перехода, равное 2. Время перехода при кодировании определяется минимальным временем между изменениями входных сигналов и скоростью функционирования последовательностной цепи (предполагается работа в основном режиме).

характер Rj и Rj гарантирует, что это всегда может быть сделано.

Пример 4.5. Кодирование с помощью мнолества связанных строк для таблицы переходов, приведенной на рис. 4.13, показано на карте Карнау и в таблице, представленной на рис. 4.14. Стрелки указывают, как выполняются два перехода. Если цепь является устойчивой в состоянии 6, представленном кодом 1010 на рис. 4.14, а, и входах 11, то первый щаг перехода будет

Использование кодирования с помощью множества связанных строк с минимальным числом переменных требует весьма тщательного анализа. Следующий пример показывает, как может быть получено кодирование для заданной таблицы переходов.

Пример 4.6. На рис. 4.15, а и б показаны таблица переходов и требуемые условия смежности, которые должны быть удовлетворены с помощью различного множества строк. Поскольку имеется щесть состояний, необходимы по крайней мере три переменные при любом кодировании состояний. Вначале присвоим произвольный код, скажем ООО, состоянию 2, которое имеет наи-больщее число смежностей. Любая точка в -кубе имеет только k точек, смежных с данной. Так как для состояния 2 необходимы четыре смежных состояния, то кодирование только тремя переменными является недостаточным для этого состояния. Если присвоить второй код, смежный с первым, то два кода вместе дадут четыре смежные точки, которые могут быть присвоены состояниям 1, 3, 4 и 6. Одно возможное кодирование для состояния 2 и четырех смежных с ним состояний показано на рис. 4.15, в.

Теперь состояние 5 должно быть смежным с состояниями 1, 3 и 4, а также требует присвоения кода 110 для этого состояния и кода 111 для состояния 3. Таким образом, должно быть сформировано множество связанных строк для состояния 3. Проверяя таблицу переходов, можно убедиться, что все требуемые условия смежности были удовлетворены. Полное кодирование состояний показано на рис. 4.15, г. Поскольку кодирование требовало только трех переменных состояний, оно происходило с минимальным числом переменных. Процесс поиска не всегда происходит столь гладко. На рис. 4.15, (Э показано другое кодирование для состояния 2 и смежных с ним четырех состояний. Так как состояние 5 должно быть смежно с состояниями 1, 3 и 4, то оба неиспользованных кода должны быть присвоены состоянию 5. Однако требование, чтобы состояние Збыло смежным с состояниями 2 и 6, не может быть удовлетворено и не представляется возможным получить кодирование множеством строк с тремя переменными. Другое удовлетворительное решение по кодированию с помощью множества связанных строк представлено на рис. 4.15, е.

Иногда можно модифицировать таблицу переходов таким образом, чтобы уменьшить число условий смежности, которые должны быть удовлетворены, и число переменных состояний, требуемых при кодировании состояний с помощью множества связанных строк. Рассмотрим таблицу переходов с однократным изменением выхода, в которой N(q{, Ij) =N{qk, Ij) = qm.

в

>2

г

Рис. 4.15. Получение кодирования состояний с помощью множества связанных строк.

где <7т не равняется qi или qu. Если модифицировать таблицу, выполняя N{qi,Ij) = qk, оставляя при этом N{qh,Ij) = qm, то в поведении автомата не произойдет изменения, за исключением того, что переход qx-в столбце Ij заменяется на переход