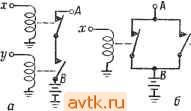о о о

У JX XJ jy.

Рис 1 3. Реленио-контактные цепи

переменная л:,- может ассоциироваться с контактом, который замыкается при Х{- 1, а переменная Xj - с контактом, который замыкается при Xj = 0. Физически это соответствует возбуждению реле булевыми переменными в порядке, обеспечивающем реализацию булевых функций. Контакты реле, соответствующие основным переменным (лг), считаются нормально разомкнутыми (т. е. размыкаются, когда переменные равны 0), а контакты, соответствующие дополнительным переменным (xf), считаются нормально замкнутыми (т. е. размыкаются, когда переменная равна 1).

При последовательном соединении двух контактов контур будет замкнут только в том случае, когда оба контакта замкнуты. Это условие описывается выражением х^хг, где Хи лгг -переменные, соответствующие рассматриваемым контактам. Параллельное соединение тех же контактов описывается выражением *1 + х2, так как контур между рассматриваемыми зажимами замкнут, если замкнут хотя бы один из них.

На рис. 1.3, е и г показаны контактные цепи, реализующие выражения ху и х-\- у соответственно. Функции принимают значение 1 только в том случае, когда контур между зажимами Л и В замкнут. При этом предполагается, что контакты приводятся в действие от реле, рабочие обмотки которых показаны на рис. 1.3, а и б. Обычно рабочие обмотки на схемах не

НИЯ булевой алгебры для переключательных цепей и был связан с релейными цепями [17].

Хотя эти цепи уже не используются в ЭВМ, они находят применение в целом ряде цепей управления. Техника проектирования контактных цепей применима и для других типов двунаправленных цепей (в отличие от цепей, построенных на логических элементах, являющихся элементами направленного действия, в этих цепях ток может протекать в обоих направлениях).

Функция, реализуемая контактной цепью, принимает значе-чие 1, если контур между рассматриваемыми зажимами замкнут. При этом предполагается, что коммутация контактов осуществляется под действием входных переменных функции. Так,

) Цепь считается имеющей обратную связь при наличии контура, связывающего выход логического элемента G с его входом (даже если этот контур содержит другие логические элементы).

показываются и контактные цепи изображаются как показано на рис. 1.3, е и г.

Методы анализа и синтеза переключательных цепей, построенных как на логических элементах, так и на реле, аналогичны. Поэтому ниже мы будем рассматривать в основном переключательные цепи, содержащие логические элементы, обращая внимание только на наиболее интересные специальные случаи реализации контактных цепей.

Методы анализа и синтеза контактных цепей могут быть использованы для проектирования некоторых цепей с МОП-транзисторами. При этом комбинационная функция реализуется схемой с выходным полевым транзистором, управляемым другими полевыми транзисторами, включенными по последовательно-параллельной схеме. Выходной транзистор дополняет функцию, реализуемую последовательно-параллельной схемой. Как и в контактных цепях, логические элементы И и ИЛИ реализуются соответственно последовательными и параллельными соединениями.

1.3. КОМБИНАЦИОННЫЕ ЦЕПИ

Переключательная функция со входами х = (лгь лгг, ..., а: ) называется комбинационной функцией, если ее выход z зависит только от текущих значений х. Реализацией комбинационной функции называется комбинационная цепь. В этом разделе мы рассмотрим задачи анализа и синтеза комбинационных цепей.

i.3.1.АНАЛИЗ КОМБИНАЦИОННЫХ ЦЕПЕЙ

Задача анализа комбинационных цепей состоит в нахождении функции, реализованной цепью. Функция может быть представлена в форме булевого выражения либо в форме таблицы, связывающей ее выходные величины с каждой возможной комбинацией входных величин. Такая таблица называется таблицей истинности.

Хотя для реализации комбинационных функций могут быть использованы цепи с обратными связями), ниже рассматриваются только ациклические цепи (т. е. цепи без обратной связи), так как с помощью этих цепей можно реализовать любую комбинационную функцию и, кроме того, они легко поддаются анализу с помощью лемм и теорем двузначной булевой алгебры, рассмотренных в предыдущем разделе.

з-Г

Рис. 1.4. Комбинационная цепь.

полученных выражений с помощью законов булевой алгебры. Для цепи, изображенной на рис. 1.4,

G4 = Сг + Оз = 2 +3 + Х3Х4,

Gg = Gi G4 = Gi -Ь G4 = Х1Х2 + XzXs (% + Х4) =

== Х1Х2 -jr 2X3X4.

Из последнего выражения следует, что выходная переменная представляет собой сумму произведений входных переменных и равна 1 только в том случае, если все переменные, входящие в одно из слагаемых, равны 1. Отсюда следует, что выходная переменная равна 1, если xi = Хг - О или если х2 - Хъ = I, а х4 = 0. Анализ цепи может быть проведен и в обратном порядке, т. е. от выхода к входам.

Значение выходной переменной G5 для любой комбинации входных переменных может быть определено подстановкой входных переменных в ее булево выражение.

Результаты анализа, проведенного этим методом, сводятся в таблицу истинности, которая для рассматриваемой цепи

Процедуру анализа ациклической цепи продемонстрируем на примере цепи, изображенной на рис. 1.4.

Используя для обозначения выходов логических элементов Gi переменные Gi, для логических элементов со входами Xi получим

G, =Xi+ Х2,

G2 = Хгз = 2 4

Gg = 3X4.

Выражение для выходной переменной цепи находится путем вычисления выходов логических элементов G4 и Gs и упрощения

Рис. 1.5. Таблипа истинности для цепи, изображенной на рис. 1.4.

одно из двух значений, то для функции п-переменных таблица истинности должна содержать 2 строк.

1.3.2. СИНТЕЗ КОМБИНАЦИОННЫХ ЦЕПЕЙ

Рассмотрим задачу синтеза комбинационных цепей. При этом будем исходить из того, что логические характеристики комбинационной функции двоичных переменных Ху, Хг, Хп заданы в виде таблицы истинности. Множество 2 возможных значений переменных Хи Хг, Хп образуют п-мерное пространство (или сокращенно п-куб). Для каждого из этих 2 значений переменных, рассматриваемого как точка в п-кубе (п-мерном пространстве), функция / может принимать значение, равное либо 1 {1-точка, или, что то же, точка 1), либо О (О-точка, или, что то же, точка 0), либо быть неопределенной (безразличная точка). Неопределенность выходной переменной для конкретной входной комбинации означает, что эта комбинация никогда не будет иметь место или что выходная переменная может равняться либо О, либо 1.

Говорят, что цепь реализует функцию f, если ее выход равен 1 для каждого входа, соответствующего точке 1, и равен О для каждого входа, соответствующего точке 0. Выход, соответствующий неопределенной точке, может быть равен либо О,

представлена на рис. 1.5. В это?) таблице для каждой возможной комбинации входных переменных предусмотрена отдельная строка. Так как каждая входная переменная может принимать

либо 1- Хотя для некоторой комбинации входных переменных комбинационная функция может быть не определена, цепь, реализующая эту функцию при подаче на ее вход рассматриваемой входной комбинации, в зависимости от способа реализации даст на выходе либо О, либо 1.

На рис. 1.6,0 показана таблица истинности для трех функций fl, f2> fs с входными переменными Xi, Х2, Xs. Неопределенные

X, Xs

Рис. 1.6 Таблица истинности (а) и схемная реализация fi и fi (б).

состояния функций отмечены в таблице знаком - . Цепь на рис. 1.6,6 с выходом F представляет собой реализацию функций h и fs, так как fi{xu Xz, Хз)=Р(х1, Xg, Xs) и fzixu Xs, Хз) = = F{xi, X2, Xs) везде, где /2 определена.-Однако эта цепь не является реализацией функции /з, так как F(0, О, 0) = 0, а f3(0. О, 0)= 1. Вообще одна и та же комбинационная цепь может быть использована для реализации двух комбинационных функций fi и /j, если отсутствует входная точка х^, такая, что fi{h)= 1, а fj{\k) = О или наоборот.

Каждая точка п-куба, определенного переменными {1, Х2, ..., Хп], может быть представлена в виде терма полного >гроизведения, т.е. произведения, содержащего переменные или

ИХ дополнения. Такой терм равен единице только для этой точки и называется минтермом. Строки таблицы истинности удобно обозначать целыми числами, соответствующими данной комбинации, если последняя рассматривается как двоичное число (при условии, что ЛГ] определяет наибольший значащий разряд). Обозначая минтерм, соответствующий строке с индексом i, через rrii, для П = 3 получим /По - Х\Х2Хъ, тз = Х1Х2Х3.

Если задана комбинационная функция то ее простая схемная реализация может быть получена представлением каждой 1-точки соответствующим минтермом и суммированием последних. Такая реализация называется канонической суммой мин-термов. Каждый минтерм реализуется логическим элементом И, на входы которого могут подаваться как х, так и х. Суммирование выполняется с помощью логического элемента ИЛИ.

Рассмотрим другую форму канонической реализации комбинационной функции f. Для этого представим в виде минтермов функцию f: f = S mi, где /о -множество индексов строк, со-

ответствующих точкам О функции / (или точкам 1 функции /). Используя законы Де Моргана, получим для f

f= П Ml,

где Mi = m, представляет собой терм полной суммы, или макс-терм. Он равен нулю только для строки с индексом L Полученная реализация называется каноническим произведением макс-термов. Каждый макстерм реализуется логическим элементом ИЛИ, а произведение макстермов - логическим элементом И.

Пример 1.1. Для функции /1 (рис. 1.6, а) каноническая сумма минтермов равна

/1 = Х1Х2Х3 -\- X1X2XS + 1X23 Ь Х1Х2Х3 = = mi + /Пз -Ь Шб + /П7.

Каноническая сумма минтермов функции f\ равна

fl = X1X2XS + Х1Х2Х3 + Х1Х2Х3 + Х1Х2Х3 = = /По + ms + /П4 + /Пб.

С помощью законов Де Моргана последнее выражение легко преобразовать в каноническое произведение макстермов функции /1

f 1 == (Xl + Х2 + Хз) {Xi + Х2 + Хз) {Xi + Х2 + Хз) {Xi + Х2 + х- =

= Мо-M2-MiM5.

Рассмотренные канонические реализации называются двухступенчатыми, так как максимальное число логических элемен-

f == Х1Х2 -f Х1Х2

Рис. 1.7. Таблица истинности комбинационной функции.

ности на рис. 1.7, после упрощения с помощью законов булевой алгебры может быть представлена только одним минтермом

f = Х1Х2 + Х1Х2 = Xi {Х2 + X2i - Xi- \=Xi.

Рассмотрим задачу получения реализаций комбинационных функций, удовлетворяющих определенным критериям оптимальности. Так как частные критерии осуществимости той или иной реализации зависят от технологии изготовления цифровых цепей, мы остановимся только на двух простых случаях, поддающихся математическому описанию. Это - минимизация числа логических элементов в цепи, включающая выбор из всех цепей с минимальным числом логических элементов цепи с минимальным числом логических входов, и минимизация числа логических входов цепи. Двухступенчатые реализации будем искать в виде суммы произведений, предполагая, что каждому входу соответствуют и переменная Xi, и ее дополнение Xi. Такие входы называются парафазными в отличие от однофазных входов, для которых в качестве входной переменной выступает только основная переменная л:,-. В общем случае получение двухступенчатой реализации произвольной комбинационной функции при наличии только однофазных входов не представляется возможным.

В двухступенчатой реализации в виде суммы произведений (М-ИЛИ) логические элементы И используются для получения

тов, через которые проходит входной сигнал, равно двум (при этом не учитываются инверторы, которые могут оказаться необходимыми для выполнения операции отрицания, т. е. образования дополнительных входов). Так как обычно каждый логический элемент характеризуется запаздыванием, то быстродействие цепи пропорционально числу ступеней. Поэтому двухступенчатые цепи считаются относительно быстродействующими. С помощью основных законов булевой алгебры канонические двухступенчатые реализации могут быть упрощены. Реализации, получаемые в результате такого упрощения, называются минимальными двухступенчатыми реализациями. Например, каноническая сумма минтермов функции, заданной таблицей истин-

) Условие, что импликанта должна покрывать хотя бы одну точку 1, вводится для того, чтобы избежать распространения понятия простой импликанты на случай, ксгда терм-произведение покрывает только неопределенные точки. Такие импликанты, очевидно, не представляют интереса для задач реализации, так как покрытые ими точки могут рассматриваться как точки О, дающие реализации с меньшим числом членов.

произведений литералов (под литералом понимается либо сама переменная Хг, либо ее дополнение Xi). Операция суммирования выполняется с помощью логического элемента ИЛИ, на входы которого поступают произведения, сформированные на выходах элементов И. В отличие от минтермов все литералы не обязательно должны появляться в каждом терм-произведении суммы. Терм-произведение Р, в котором некоторые переменные не появляются, определяет несколько точек в п-кубе. Говорят, что эти точки покрыты Р. Например, для входных переменных х\, Х2, Хг- терм Х1Х3 покрывает две точки xi = 1, лгг = О, лгз = О и xi = 1, А'2 = 1, лгз = О, соответственно обозначенные (1, О, 0) и (1, 1,0). Терм Xl покрывает четыре точки (О, О, 0) (О, О, 1), (О, 1, 0) и (0,1,1). Вообще терм-произведение, содержащий k литералов, покрывает в и-кубе 2 - точек, так как каждый литерал, не содержащийся в этом члене, может быть либо О, либо 1. Иногда говорят, что такой терм представляет {п - к)-куб. В соответствии с этой терминологией минтерм представляет 0-куб.

Говорят, что терм-произведение Р является импликантой функции f, если он покрывает хотя бы одну точку 1 этой функции и ни одна из точек, покрытых Р, не является точкой О этой функции, т.е. импликанта функции покрывает только точки 1 и, возможно, некоторые неопределенные точки. Импликанта Pi функции f называется простой импликантой этой функции, если для любой другой импликанты Рг существует некоторая точка, которая покрыта Pi (но не Р2) Если из простой импликанты вычеркнуть любой литерал, то результирующий терм-произведение уже не будет являться импликантой функции.

Пример 1.2. Рассмотрим функцию /, заданную в виде таблицы истинности, приведенной на рис. 1.8. Терм-произведение Pi=zXiX2 покрывает точки (О, О, 0) и (О, О, 1). Так как для обеих этих точек f = 1, то Р есть импликанта f. Однако Pi не простая импликанта f, так как Р2 = Х\ есть импликанта f и каждая точка, покрытая Pj, также покрыта Рг-

Рассмотрим теперь двухступенчатые реализации вида И-ИЛИ, минимизирующие общее число логических входов цепи.

Лемма 1.9. В минимальной двухступенчатой реализации вида И-ИЛИ комбинационной функции f выход каждого логического элемента И есть терм-произведение, являющийся простой импликантой f.

Рис- 1.8 Таблица истинности для примера 1.2.

реализующим Рг, причем новая цепь также реализует рассматриваемую функцию f.

Следствие 1.1. В минимальной двухступенчатой реализации вида И-ИЛИ комбинационной функции f выход каждого логического элемента И является простой импликантой и каждая точка 1 функции f покрывается хотя бы одной из этих простых импликант.

Доказательство. Предлагается выполнить самостоятельно в виде упражнения.

Из доказанной выше леммы и следствия 1.1 вытекает следующая процедура решения задачи получения минимальной двухступенчатой реализации вида И-ИЛИ функции f.

Процедура 1.1

1. Найти полное множество простых импликант функции f.

2. Из этого множества выбрать подмножество минимальной стоимости, покрывающее все точки 1 этой функции.

Понятие стоимость простой импликанты связано с критерием оптимизации. Так, в задачах минимизации числа логических элементов при схемной реализации комбинационной функции f стоимость каждой простой импликанты с двумя или более литералами принимается равной 1, а стоимость каждой простой импликанты с одним литералом -О (так как для ее реализации не требуется элемент И).

Доказательство. Предположим, что существует минимальная двухступенчатая реализация вида И-ИЛИ функции f и выход G каждого логического элемента представляет собой терм-произведение Р\, не являющийся простой импликантой. Тогда должна существовать другая импликанта Рг, покрывающая все точки, покрытые Ри и имеющая меньшее число литералов, чем Р\. Поэтому логический элемент И, реализующий Pi, может быть заменен логическим элементом И с меньшим числом входов.

) Нанесение меток необходимо для того, чтобы избежать образования терм-произведения, покрывающего только неопределенные точки,

В задачах минимизации общего числа входов логических элементов стоимость простой импликанты принимается равной w{Ph)+ 1, где tiy(Pft) - число литералов Р^, если ш(Рй)= 1. Она складывается из w{Pk) входов логического элемента И, реализующего Ри, и входа логического элемента ИЛИ. Если w{Pfi)~ 1, стоимость Ph равна 1, так как для реализации простой импликанты не требуется логический элемент И. Стоимость множества простых импликант равна сумме стоимостей каждой из них.

С помощью правила ху -f- ху - у, позволяющего исключить литерал х, можно сформировать импликанту, покрывающую две точки 1 (или точку 1 и неопределенную точку), отличающиеся друг от друга только одним литералом х. Последовательное повторение этой операции позволяет получить простые импликанты.

Квайном и Мак-Класки [И, 16] предложена следующая процедура получения простых импликант этим способом. Процедура 1.2

1. Составить таблицу для всех 1-точек и неопределенных точек функции f, разбитых на классы So, Sj, S2, S , где 5, содержит все такие точки с i входными переменнььми, равными 1, и п - i переменными, равными 0. Элемент таблицы, соответствующий минтерму tUi, является бинарным представлением i. Пометить каждую точку для разделения 1-точек и неопределенных точек функции').

2. Сравнить каждый элемент в с каждым элементом Si +1 для всех i, О t п. Для пар, отличающихся только на один литерал Xj, образовать новые импликанты, покрывающие обе точки. Эти импликанты неопределенны для Xj, а оставшиеся переменные сохраняют те же значения, что и в паре комбинируемых термов (строк). Новые импликанты поместить в класс Sl, а термы, использованные для их образования, пометить знаком V - Присвоить каждой новой импликанте метку 1, если хотя бы один из термов, использованных для ее образования, имеет метку 1. Если оба терма, использованных для образования новой импликанты, имеют неопределенные метки (-), то эта же метка присваивается новой импликанте.

3. Повторить шаг 2, используя Sl и St+i для образования S7. Аналогично образовать Sf из S и Sl+i и продолжать эту процедуру до тех пор, пока дальнейшие комбинации окажутся невозможными. При этом неопределенные переменные комбинируемых термов сохраняют неопределенность и во вновь образованных импликантах.