= mimztrismiOOO. Последовательность T-N для ошибки в любом разряде i определяется из импульсной реакции функции Т -. Если Z -импульсная реакция функции, то TN для ошибки в i-M разряде характеризуется величиной О^-(г), где самый левый разряд соответствует t =: 1. Импульсная реакция Т- определяется выражением

х: 1000000000...

Dz: 0001110100...

Dz: 0 1110 10 0 11...

z: 1 1 1 О 1 О О 1 1 I ...

Импульсная реакция представляет собой выходную циклическую последовательность 2=111010011..... Реакция на импульс помехи, появляющейся при t=i, 1 t 7, показана в таблице на рис. 3.49. Заметим, что разряды 5-7 последовательности 7-W в каждом из этих случаев различны. Следовательно, эти три разряда однозначно определяют T~N, которая может быть реализована многовыходовой комбинационной цепью с тремя входами. Сложение по модулю 2 выходов этой цепи с М* позволяет получить М. Например, если M*= 1100101, то последние три разряда показывают (рис. 3.49), что =0011101 и

M = M* + r~iV = 1111000.

Рис. 3.49. Реакция иа пульсы помехи.

Следует отметить, что одна ошибка в выходе кодирующего устройства

может привести к тому, что несколько разрядов М* будут отличаться от М, но они также исправляются этим методом.

3.4. РЕГУЛЯРНЫЕ ВЫРАЖЕНИЯ

Проблема нахождения функции, реализованной таблицей состояния и нахождения таблицы состояния, соответствующей словесному описанию функции, иногда может быть эффективно решена с помощью регулярных функций. Регулярной функцией называется представление множества последовательностей. Говорят, что для последовательностного автомата М с одним двоичным выходом Z входная последовательность принимается М В указанном исходном состоянии, если автомат формирует

о 1

Рис 3.50 Две таблицы состояний

Рис. 3j51. Таблица состояний с множеством сигналов Ф

ИЗ бесконечного множества последовательностей перемежающихся нулей и единиц, начинающихся с нуля и кончающихся единицей.

Возможно, что множество сигналов S автоматов не содержит последовательностей, т. е. отсутствует входная последовательность, которая, будучи приложена к автомату в заданном исходном состоянии, даст на выходе 1. Например, множество сигналов таблицы состояний на рис. 3.51 в исходном состоянии 2 - пустое и обозначается как Sz - Ф.

Для автомата, приведенного на рис. 3.51, с исходным состоянием 1 выход равен 1 при отсутствии входа. Этот случай может трактоваться как наличие входной последовательности % длиной 0. Для автомата, показанного на рис. 3.51, в исходном состоянии 1 множество сигналов равно Si = {?,}. Важно заметить разницу между пустым множеством сигналов Ф и последовательностью длиной 0. Пустое множество не содержит никаких последовательностей, включая X.

Множество последовательностей, принятых конечными последовательностными автоматами, может быть представлено регулярными выражениями. Множество последовательностей, представленных регулярными выражениями, называется регу-лярны.и множеством. Регулярное множество для входного алфавита / рекурсивно определяется следующими правилами:

ВЫХОД z== 1 для последнего входа этой последовательности. Входная последовательность, принимаемая М в исходном состоянии 9о. называется последовательностью сигналов М для исходного состояния 9о- Множество всех последовательностей сигналов автомата М называется его множеством сигналов. Автомат, имеющий более одного двоичного выхода, обладает множеством сигналов, ассоциированным с каждым выходом. Для таблицы состояний Ml, приведенной на рис. 3.50, а с исходным состоянием 1 множество сигналов равно S = {1,01}. Множество сигналов для таблицы на рис. 3.50, б в исходном состоянии I состоит

1. Если f е /, то i - регулярное выражение и /? = г представляет собой входную последовательность i.

2. Если А а В являются регулярными выражениями, то A\j В есть регулярное выражение, которое представляет все входные последовательности, представленные А или В.

3. Если Лив являются регулярными выражениями, то д.В = {ху\х^А, уеВ} есть регулярное выражение, представляющее множество последовательностей, сформированных каскадным включением каждой входной последовательности х в А, следующей перед каждой входной последовательностью у в В. Для удобства А-В будем ниже записывать в виде (А) (В) или, если Л и В - единственные символы, просто в виде АВ.

4. Если Л -регулярное выражение, то Л*=:?илиЛ-Ли и Л-Л-Л и ... - также регулярное выражение.

Пример 3.25. Для входного алфавита {О, 1}, R = 0*1 [О U и 1(0)*!]* - регулярное выражение. Входная последовательность 001011 представляется R как 10 и 1. Однако входная последовательность 11 не представляется R. Регулярное выражение (0U1)* представляет все входные последовательности, включая К, а регулярное выражение (О U 1)(0LJ 1)* -все входные последовательности, исключая К.

Регулярное выражение может быть использовано как промежуточный щаг при выводе таблицы состояний по словесному описанию проблемы. Рассмотрим, например, вывод таблицы состояний, которая образует выход 1 для любой последовательности, содержащей нечетное число единиц и не содержащей нулей. Регулярное выражение R, определяющее это множество последовательностей, равно R - \ (И)*. Множество входных последовательностей, не содержащее трех последовательных нулей, представляется выражением /? = [1* (01 U 001) *] *. Иногда регулярное выражение вывести нелегко. Например, множество R последовательностей, не содержащих подпоследовательностей нулей нечетной длины или подпоследовательностей единиц четной длины, равно

/? = [1 (11)* 00 (00)*]* и [00 (00)* 1 (11)1* и 1 (11)*.

Алгоритмы для вывода регулярного выражения из словесного описания последовательностного автомата отсутствуют. Выражения, приведенные выше, были сконструированы исходя из того, что выражениями представляется каждая желаемая последовательность сигналов. Таким образом, для представления одного и того же множества последовательностей можно получить различные регулярные выражения. Однако, когда регулярное выражение выведено, таблица состояний конечного автомата с множеством последовательностей R может быть

построена по любому из этих регулярных выражений. Если два выражения эквивалентны, то эквивалентны и таблицы состояний, построенные на их основе.

3.4.1. ВЫВОД ТАБЛИЦЫ СОСТОЯНИЙ ИЗ РЕГУЛЯРНОГО ВЫРАЖЕНИЯ

Если задано регулярное выражение R, то можно построить таблицу состояний для функции, которая генерирует на выходе 1 из заданного исходного состояния тогда и только тогда, когда входная последовательность X е /?. Эта процедура иллюстрируется для выражения R = [1 *0(1 U 01)]*.

Обозначим различные точки последовательности различными буквами:

= s[iA(icUoW

Состояние автомата М будет соответствовать буквенным индексам R. Входная последовательность Хе/? должна перевести М из исходного состояния S в конечное состояние С или Е. Если X - префикс входной последовательности в R, то X должен перевести М из S в А, В, С, D или Е в зависимости от положения R, соответствующего X. Наконец, если X - не префикс любой из последовательностей в R, то ни одна из последовательностей с X в качестве префикса не образует выход!. Мы достигнем этого, потребовав, чтобы последовательность X перевела автомат М в состояние Т, называемое ловушкой. Автомат, попавший в это состояние, не может его оставить, и все последовательные выходы равны 0. Состояние Т не соответствует ни одному из буквенных индексов в R, но каждое из остальных состояний будет соответствовать одному из этих индексов. Для регулярного выражения в нашем примере входная последовательность должна перевести автомат М из исходного состояния 5 в В, а входная последовательность 011 -в ловушку Т.

Таблица состояний автомата Мура, которая принимает регулярное множество, представленное регулярным выражением R, может быть построена с помощью буквенных индексов R. Исходное состояние автомата соответствует индексу S в этом выражении. Так как KR, то выход, ассоциированный с состоянием S, равен 1. Из индексов в регулярном выражении следует, что состояние, ассоциированное с индексами С и Е, должно также иметь выход 1, а все другие состояния должны иметь выходы 0.

Элементы следующего состояния в таблице состояний теперь могут быть охарактеризованы с помощью индексов в регулярном выражении. Обозначив состояния индексами в регулярном выражении, получим N{S,0) = B и N(8,1) - А. Входные по-

S АЕ BE CD В Т

Рис. 3.52. Таблица состояний, соответствующая данному регулярному выражению R.

Рис. 3.53. Таблигш состояний, соответствующая регулярному выражению R.

Для рассмотренного выше регулярного выражения R мы имели возможность проиндексировать каждое положение, так что если входная последовательность x была префиксом последовательности, представленной R, то x однозначно определяет последовательность индексов. Это свойство делает возможным построить таблицу состояний с состоянием, соответствующим каждому индексу в регулярном выражении. Однако не всегда удается получить таблицу состояний таким способом.

Рассмотрим регулярное выражение

/? = о(ои 1)* 1U0*. Индексируя R как указано выше, получим = 5 0л(ОвиуМ^ио;,.

Если начать с индекса S и входа О, следующий индекс в регулярном выражении может быть А или Е. В таблице состояний это может быть представлено состоянием, соответствующим и Л и £ (обозначено АЕ) и характеризующим N{S, 0) = АЕ. Так как в R нет последовательности, начинающейся со входа 1, то N{S, I) = Г -ловушка. Из регулярного выражения следует, что входная последовательность 00 может вести к положениям

следовательности 00 и 10 переводят автомат в состояния D и В соответственно. Следовательно, {В, 0) - D, а N (Л, 0) ~ В. Оставшиеся элементы в таблице состояний заполняются аналогично, давая таблицу состояний, приведенную на рис. 3.52. Заметим, что N{D,0) = Г -ловушка, так как последовательность, начинающаяся с ООО, не может быть представлена регулярным выражением R.

oU i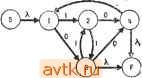

Рис. 3.54. Таблица состояний (а); граф перехода состояний (б).

приведен на рис. 3.54,6. Ветви, обозначенные через X, идут от 5 к узлу, соответствующему исходному узлу автомата, и от всех состояний, формирующих выход 1, к узлу F. (Для автомата Мили, переход от состояния qi, вход Ij, результирующийся в получении выхода 1, должен быть представлен двумя ветвями, обозначенными Ij, от qi к N {qi, Ij) и от qi к F.)

В или Е. Это требует, чтобы N(AE,0) - BE. Вообще если состояние соответствует множеству индексов в регулярном выражении, то следующее состояние для любого входа соответствует множеству индексов следующих положений в этом выражении. Таблица состояний автомата, принимающего последовательности, представленные R, приведена на рис. 3.53. Положения с индексами S, D и Е должны иметь выходы 1. Следовательно, состояния S, АЕ, BE и CD имеют в таблице состояний выходы ].

Любое регулярное выражение, которое может быть индексировано k символами (включая S), может быть реализовано последовательностным автоматом с максимум 2- + 1 состояниями. Состояния соответствуют исходному состоянию S, ловушке Т и 2- - 1 непустым подмножеством k - 1 символов. Этот автомат может быть упрощен. Аналогичным образом можно вывести автомат Мили, соответствующий регулярному выражению R. Однако если Я е i?, то автомата Мили, соответствующего R, не существует.

3.4.2. ВЫВОД РЕГУЛЯРНОГО ВЫРАЖЕНИЯ ИЗ ТАБЛИЦЫ СОСТОЯНИЙ

Теперь опишем метод вывода регулярного выражения из таблицы состояний автомата Мура, используя в качестве примера таблицу на рис. 3.54, а. Граф перехода, соответствующий заданной таблице состояний с дополнительными узлами S я F,

Рис. 3.55. Упрощенный граф перехода состояний.

F, осталось неизменным. Если привести граф к виду, показанному на рис. 3.55, то множество последовательностей, принятое

автоматом, имеет вид RiRzRs-

Основное правило для упрощения этого графа -исключение узлов - показано на рис. 3.56. Мы исключаем узел Ns из графа на рис. 3.56, а и изменяем обозначение ветвей как показано на рис. 3.56,6. Легко проверить, что множество последовательно-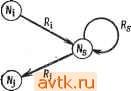

о

Рис. 3.56. Основное упрощение путем исключения узла

стей, определенных переходами между любой парой состояний (отличных от As), осталось неизменным. Вообще если в исходном графе имеется ветвь Ru направленная от Л^ к Ns, ветвь R, направленная от Ns к i?,-, и замкнутый контур Rs на узле Ns, то упрощенный граф содержит ветвь, направленную от Л^г к Nj и обозначенную RiRsR,-- Отметим, что Л^,- может быть идентичен Л^г. При этом в графе появится замкнутый контур на узле Nu обозначенный RiRIRj. Если узел Rs не имеет замкнутого контура, то ветвь от Л^г к Nj будет обозначена RiRj.

На рис. 3.56,6 показано, как узел Ns может быть исключен из графа на рис. 3.56, а. Эта основная процедура упрощения (исключение узла) может применяться последовательно до тех пор, пока граф не примет вид, показанный на рис. 3.56,6.

Легко видеть, что все входные последовательности, дающие последний выход, равный I, соответствуют путям от 5 к F, и каждый такой путь соответствует одной из таких последовательностей. Каждая ветвь имеет индекс, который представляет собой регулярное выражение. Теперь упростим граф так, чтобы множество последовательностей, определенных путями от S к

Применение упрощающей процедуры к графу на рис. 3.54, б, повторенному на рис. 3.57, а дает последовательный ряд упрощений, показанный на рис. 3.57, б, в и г, заключающихся в по-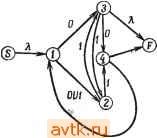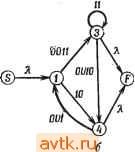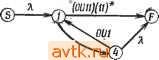

wu(omi)(iif(ouw)

(ouii)lifuwuiouiiXu)*(Daw} - Ч [юи(оШ1)(иГ(оию)](ои1)

в г

Рис. 3.57. Упрощение графа перехода состояний.

следовательном исключении узлов 2, 3 и 4. Результирующее регулярное выражение имеет вид

/?=([1ои(оии)(11)* (ouio)](oui)r [{oun)(iiruiou

U(oun)(nr(ouio)].

При различном порядке исключения узлов получаются различные, но эквивалентные регулярные выражения. Эквивалентность двух регулярных выражений или таблиц состояний, соответствующих этим выражениям, может быть продемонстрирована с помощью алгебраических преобразований.

Мы показали, как построить таблицу состояний по заданному регулярному выражению и как вывести регулярное выражение, представляющее последовательности, принятые последовательностным автоматом, из его таблицы состояний. Из этого следует, что множество последовательностей, принятых конечным последовательностным автоматом, является регулярным множеством.

В гл. 1 было указано, что существуют последовательностные функции, не реализуемые конечными автоматами. Последова-

тельности, для которых такие функции дают выход 1, не могут быть представлены регулярными выражениями, так как функции не могут быть реализованы конечными автоматами.

БИБЛИОГРАФИЯ И КОММЕНТАРИИ

Основной материал по минимизации состояний для неполностью определенных таблиц взят у Паулла и Унгера [15]. Гинзбург [7] показал, что величина наибольшего максимального несовместимого множества представляет собой нижнюю границу числа состояний. Грасселли и Люссио [9] ввели понятие классов простых совместимых множеств, а Унгер [18] описал технику упрощения некоторых импликационных графов. Кобхэм и др. [3] показали, что эта проблема может быть сформулирована как задача целочисленного линейного программирования. Грасселли и Люссио [8] рассмотрели проблему сокращения числа столбцов таблицы состояний. Мур [14] ввел понятия экспериментов с по-следовательностными автоматами. Хороший материал по этому вопросу привел Гилл [6]. Хенни [10] и Фридман и Менон [5] разработали процедуры для вывода относительно эффективных тестовых последовательностей. Материал, связанный с отсутствием потерь информации, впервые изложен Хаффманом [11]. Эвен [4] рассмотрел конечные автоматы без потери информации. Основной материал по линейным автоматам также получен благодаря Хаффману [12]. Петерсон и Вельдон [16] рассмотрели применение этих автоматов для исправления ошибок. Материал по регулярным выражениям взят у Бржозовского и Мак-Класки [2]. Кроме того, в главе имеются ссылки на Мак-Наутона и Ямаду [13] и обзор Бржозовского [1].

ЛИТЕРАТУРА

1. Brzozowski J. А., А Survey of Regular Expressions and Their Applications, IRE Trans. Electronic Computers, vol. EC-11, pp. 324-335, June 1962.

2. Brzozowski J. A., McCluskey E. J., Signal Flow Graphs and Regular Expressions, IRE Trans. Electronic Computers, vol. EC-12, pp. 67-76, April 1963.

3. Cobham A., Fridshal R., North J. H., An Application of Linear Programming: to the Minimization of Boolen Functions, Proc. Second Annual Symp. on Switching Theory and Logical Design, 1961.

4. Even S., On Information Lossless Automata of Finite Order, IEEE Trans. Electronic Computers, vol. EC-14, pp. 561-569, August 1965.

5. Friedman A. D., Menon P. R., Fault Detection in Digital Circuits, Prentice-Hall Inc., Englewood Cliffs, N. J., 1971.

6. Gill A., Introduction to the Theory of Finite State Machines, McGraw-Hill, New York, 1962; имеется русский перевод: Гилл А., Линейные последовательные машины, изд-во Наука , 1974.

7. Ginsburg S., On the Reduction of Superfluous States in a Sequential Machine, /. Assoc. Сотр. Mach., vol. 6, pp. 259-282, April 1959.

8. Grasselli A., Luccio F., A Method for Combined Rowcolumn reduction of flow tables, Proc. 7th Annual Symposium on Switching and Automat? Theory, September 1966.

1 2 3 4 5 6 Рис. 3.58. К упражнению 3.1.

3.2. Найдите минимальные таблицы состояний, эквивалентные каждой из следующих полностью определенных таблиц.

9. Grasselli А., Luccio F., A Method for Minimizing the Number of Internal States in Incompletely Specified Sequential Networks, IEEE Trans. Electronic Computers, vol. EC-14, pp. 350-359, June 1965.

10. Hennie F. C, Fault-Detecting Experiments for Sequential Circuit, Proc. Fifth Annual Symp. Switching Circuit Theory and Logical Design, pp. 95- 110, 1964.

11. Huffamn D. A., Canonical Forms for Information-Lossless Finite State Logical Machines, Sequential Machines - Selected Papers, E. F. Moore (Ed.), Addison Wesley, Reading, Mass., 1964.

12. Huffman D. A., The Synthesis of Linear Sequential Coding Networks, in Information Theory, Colin Cherry (Ed.), Academic Press, New York, N. Y., 1956.

13. McNaughton R., Yamada H., Regular Expressions and State Graphs for Automata, IRE Trans. Electronic Computers, vol. EC-9, pp. 39-47, March 1960.

14. Moare E. F., Gedanken-experiments on Sequential Machines, Automata Studies, Princeton Univ. Press, Princeton, N. J., pp. 129-153, 1956.

15. PauU M. C, Unger S. H., Minimizing the Number of States in Incompletely Specified Sequential Functions, IRE Trans. Electronic Computers, v l. EC-8, pp. 356-367, September 1959.

16. Peterson W. W., Weldong E. J., Error Correcting Codes, Second Edition, MIT Press and J. Wiley & Sons, Cambridge, Mass., 1972; имеется русский перевод: Петерсон У., элдон Э., Коды, исправляющие ошибки, изд-во Мир , М., 1976.

17. Unger S. Н., Simplification of State Tables, AIEE Fall Meeting, Chicago, October 1960.

18. Unger S. H., Flowtable Simplification - Some Useful Aids, IEEE Trans. Electronic Computers, Vol. EC-14, pp. 472-475, June 1965.

УПРАЖНЕНИЯ

3.1. Для диаграммы nap, изображенной на рис. 3.58, найдите все максимальные совместимые множества.