(б) Чтобы реализовать цепь с передаточной функцией Г = 1 + j £) -j- заметим, что ао = ai == 014 = 1 и аг = аз = 0. Цепь, изображенная на рис. 3.42, получена из канонического представления (рис. 3.40) путем вычеркивания связей и сумматоров по модулю 2 везде, где а, = 0.

Рис 3.42. Цепь без обратной связи к примеру 3.18 (б).

Передаточные функции также удобно использовать для анализа и синтеза линейных цепей с обратными-связями. Если дана линейная цепь с переменными состояния и выходами, определяемыми уравнениями

п к

п к

то каждый выход Zi может быть представлен как линейная функция входов X, предыдущих значений х и предыдущих значений Zi. Для линейной цепи с одним входом, одной переменной состояния и одним выходом

У = ал; + рг/. (1)

z = yx-\-6y. (2)

Применяя оператор D к уравнению (1), получим

= г/ = aDx -f Dy. Следовательно, у-\- Dy = aDx,

у 1 -f PD Подставляя в уравнение (2), получим

= +

2(l-f р/)) = ул:(1+р/)) + баДл;, - -z-\-Dz==-yx-yDx.-\-baDx,

2 == + yP -f ба Ол; -f р Dz.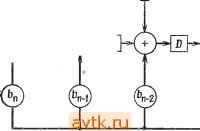

э © ®

Рис. 3.43. Каноническая линейная последовательностная цепь с обратной

связью.

влением по выходу можно изучать, рассматривая каждый выход в отдельности, а цепи с объединением по входу - с помощью принципа суперпозиции.

Последовательностная линейная цепь с одним входом и одним выходом имеет следующую передаточную функцию:

7 - g До + Д'Д + ДгД^ 4- 4- апР -

где Ui, bi = 0, 1.

Для цепи, показанной на рис. 3.43,

z = aoX + yi = а^х -f D (ajx -f b,z -f t/g) ... =

= aoX+DGiX+D2G2;+... + ITax + Db, + Dbz + ... + D%z.

Передаточная функция равна

2 flp -f а.Д -Ь АгД' 4- 4- fl P

Следовательно, эта цепь является каноническим представлением линейной последовательностной цепи с одним выходом и одним входом. (Заметим, что каноническое представление такой цепи без обратной связи соответствует частному случаю = Q

Если линейная цепь имеет k переменных состояния, то будет одновременно k линейных уравнений, аналогичных (1), которые могут быть решены для получения уравнений для переменных состояний в терминах входов х и их предыдущих значений. Затем каждый выход Zi можно выразить как линейную функцию входов X, их предыдущих значений и предыдущих значений выхода Zi. Оставшуюся часть этого раздела мы посвятим рассмотрению цепей с одним входом и одним выходом. Цепи с развет-

Рис. 3.44. Линейная последовательностная цепь.

Некоторые передаточные функции могут не соответствовать физически реализуемым цепям. Например, если Т = z/x - = (D -f- 1)/D, то Dz - {D -\- \ )х == Dx + X. Следовательно, значение 2 в момент t - 1 зависит от величины х в момент t. Такую цепь реализовать невозможно, так как в физической цепи значения z не могут зависеть от будущих значений х.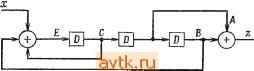

Рис. 3.45. Линейная последовательностная цепь к примеру 3.19.

Передаточная функция Т = Pi(D)/P2{D), где Pi{D) и PziD) -полиномы от D, физически реализуемы, если минимальная ненулевая степень D в PziD) не превышает минимальной степени D в Pi (D).

Если выход цепи С с передаточной функцией Т - = Pi(D)/P2 D) является входом цепи С с передаточной функцией Т' = PD)IPi{D), то передаточная функция сложной цепи равна произведению Т-Т' (предлагается доказать в качестве упражнения). Если Рз(Д) = Р2() и P4(D) = Р,(D), то Т-Т' = 1. Следовательно, выход сложного автомата равен входу (если оба физически реализуемы), и говорят, что Т' - инверсия Т, что обозначается как Т-.

Передаточная функция данной цепи легко выводится, что иллюстрируется следующим примером.

для всех i.) Если дана передаточная функция двоичной линейной функции, цепь, реализующая эту функцию, может быть вы-зедена из канонической реализации. Таким образом, если Т =

= (D2+ 1)/(D3 + D+ 1), то G3 = Gl = 0, G2 = G0=1, Ьз =

- fej = 1, Ьг = О, ai = bi - О для i 4. Реализация канонической цепи с этими значениями щ и bi показана на рис. 3.44.

Таким образом.

C + DC + DC = Dx {ГЙ + D+l)

zDC + rfC.

Dx , Dx

Z пз L г) L 1 1

D + D+l D + D+l

D + D+l

Передаточные функции цепей с несколькими двоичными входами и/или выходами выводятся аналогично.

Другой важной характеристикой функции в теории линейных систем является ее импульсная реакция. Импульсная реакция линейной двоичной цепи с одним входом и одним выходом определяется как выходная последовательность, формируемая как реакция на входную последовательность 100 ... О при предположении, что выходы всех задержек в начале равны 0. Импульсная реакция цепи может быть получена непосредственно из передаточной функции. Для цепи без обратной связи с одним входом передаточная функция имеет вид

Т = oo-v -f а, Dx + 2 + ... -f akD\

что соответствует цепи, показанной на рис. 3.40. Импульсная реакция для этой цепи равна aoaiUz ... Gfe iGfeOO ... 0.

Для цепи, изображенной на рис. 3.41, импульсная реакция равна

адОга^ОО ... = 00101000 ... 0.

В общем виде передаточная функция двоичной линейной последовательностной цепи имеет вид

Пример 3.19. Для цепи, показанной на рис. 3.45,

2 = Л + В = Л + ОЛ = DC + DC = 1>2£ + №

Е = С + В + х.

Следовательно,

C = DE = DC-\-DB + Dx==DC-\-DC-\-Dx,

СI = щ -f Z b/Q- /, < n,

Ck= Z b,C,i, k>n.

Заметим, что символы C, k> n определяют периодическую установившуюся реакцию.

Импульсная реакция может быть получена непосредственно из передаточной функции, что иллюстрируется следующим примером.

Пример 3.20. Пусть передаточная функция цепи равна

Следовательно,

{D+\)x = {D + D+l)z,

Полагая, что все предыдущие значения х и z равны О, импульсная реакция получается в виде суммы отдельных членов в последовательностях х, Dx, De и Dz, где Z)2: равно О в течение первых двух импульсов, а Dz = О в течение первых трех импульсов.

x 100000000000000

Dx 001000000000000

0 0 0 1 0 0 1 0 1 1 1 0 0 1 0

Dz 001001011100101

z 100101110010111

Входная последовательность х задана строкой 1, Dx выводится из x. Первые два выхода теперь можно получить как сумму л; -f D4 -f Dz -f Dz. Первый выход можно использовать для получения третьего значения Dz и четвертого значения Dz. Процесс повторяется до получения импульсной реакции, которая представляет собой циклическую последовательность 1110010 с периодом 7.

Теорема 3.2. Реакция линейной последовательностной цепи на произвольную входную последовательность aoOjO? ...

что соответствует канонической цепи на рис. 3.43. Импульсная реакция h этой канонической цепи определяется последовательностью символов CoCiC2C3 ... С„, где

Со == Go,

Ci = a, -f 6iCo,

C2 = G2 + b2Co + &lCi,

Сз = а +ЬзСо + Ь2С, + 6,С2, i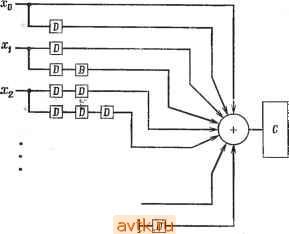

-т-ШНИ-----Ш

I-ГБМо!-----[D

Рис. 3.46. Цепь для доказательства теоре.мы 3-2.

го она генерирует импульс, задерживаемый i. Следовательно, если Xi = ai, то z = aD (h). Если входная комбинация (оо, Qi, ..., а„) подается на входы (xq, х\, ... то на входе С появится последовательность aoai ... a ООО ....

Если цепь С линейна, то вся цепь также линейна и выходная реакция на любую входную комбинацию (ас Oi, о„), приложенную к ней, идентична выходу С для входной последовательности aoUi ... а„0 ... О, приложенной к С. Пусть H{Xq, Хи Хп)-функция, реализованная всей цепью. Так как цепь линейна, то

Я(ао, Gl.....а„) = Я(аоО, .... 0) + Я(0, Gi 0)+

+ ... +Я(0, О, G ) = =aoh-aiD(h)+ ... +а„0 (/г) =

=-ZaiD4h).

... а„00 ... О может быть выражена в терминах импульсной реакции h как

где D{h) есть h, задержанная блоками i, D°{h)- h.

Доказательство. Рассмотрим цепь, показанную на рис. 3.46, и предположим, что все выходы задержек первоначально равны 0. Эта цепь в ответ на вход х{ = а, генерирует входную последовательность для С, равную 00 ... О 00 ..., т. е. если Ci= 1,

Из теоремы 3.2 следует, что реакция линейной цепи на любую входную последовательность может быть получена из ее импульсной реакции, которая в свою очередь может быть определена из ее передаточной функции.

Пример 3.21. Определим реакцию цепи в примере 3.20 на входную последовательность 1101. Передаточная функция цепи равна Т = {D-\-\)I(D-\-1), а ее импульсная реакция h показана ниже. Из теоремы 3.2 следует, что реакция на входную последовательность 1101 равна h 4-Dh-\-Dh. Эти последовательности и выходная последовательность имеют вид

h: 1001011100101110010111

Dh: О 1 О О 1 О I I 1 О О 1 О I 1 1 О О 1 О 1 1

Dh: 0001001011 10010.1 110010

z: 1100111001011100101110

Импульсная реакция цепи со сложной передаточной функцией Т может быть иногда выражена в терминах импульсных реакций подфункций Т.

Лемма 3.13. Если h - импульсная реакция цепи с передаточ-

п

ной функцией Т, то цепь с передаточной функцией Т = YTi имеет импульсную реакцию

i = \

Доказательство. Предлагается выполнить в качестве упражнения.

Теорема 3.2 и лемма 3.13 используются для вывода передаточной функции по заданной импульсной реакции.

Пример 3.22. Пусть заданная импульсная реакция равна

Л=10001011011 0.

Вспомним, что импульсная реакция h цепи с обратной связью равна hs-\-ht, где ft( - переходная составляющая h, а - периодическая установившаяся составляющая h. Для рассматриваемого случая

К=1 1 О 1 1 О 1 1 О .... /г< = 0101000....

Из леммы 3.13 следует, что если Tt имеет импульсную реакцию ht и Т^ - импульсную реакцию h, то Г = Г, -f имеет импульсную реакцию h = ha-{- ft,. Импульсная реакция

Желаемая итульшй реакция

Рис. 3 47 Линейная система к примеру 3 22.

мени, а Гг-выходную последовательность 11000... в качестве реакции на этот одиночный импульс (рис. 3.47). Следовательно, Ti = 1/ (D + 1), Гг = £> -f 1 и

окончательно

T = Tt + T,D + D +

D+l D + D + D+l

Нулевые последовательности

Реакция линейной цепи на входную последовательность, состоящую из одних нулей, представляет собой выходную последовательность одних нулей. Однако такая выходная последовательность может быть также генерирована другими циклическими входными последовательностями произвольной длины. Входная последовательность, генерирующая выходную последовательность из одних нулей, называется нулевой последовательностью. Как будет видно из дальнейшего, нулевые последовательности полезны при использовании линейных цепей для исправления ошибок.

Нулевая последовательность зависит от исходного состояния элементов запаздывания. Если вначале все запаздывания равны нулю, то последовательность одних нулей называется тривиальной нулевой последовательностью. Для произвольного исходного состояния нулевая последовательность может быть получена из передаточной функции. Если z не зависит от текущего значения д:, то для некоторых исходных конфигураций цепь может не иметь нулевой последовательности.

вызывается автоматом без обратной связи с передаточной функцией Г( = + D. Импульсная реакция состоит из повторяющейся подпоследовательности с периодом 3. Она может создаваться автоматом с передаточрюй функцией Ts = Ti-Tz, где Ti вырабатывает одиночный импульс каждые три интервала вре-

Пример 3.23. (а) Рассмотрим цепь без обратной связи с передаточной функцией r = D3+D2-f 1. Для получения нулевой последовательности положим z = 0. Тогда

zr=D4+ Dx + x = 0 и x = Dx + DH.

Положим вначале, что Dx = Dx - Dx = \. Тогда первый вход X г= £)5х + £)2х = I 4- 1 = 0. При / = 2 Dx = D4 = 1, £)x = О и второй вход также равен 0. Повторяя эту процедуру, получим следующую последовательность:

D4 Dx Dx X

1 1 1000100111

Заметим, что последовательность становится циклической после того, как в ней повторяются начальные условия.

(б) Рассмотрим цепь с обратной связью, передаточная функция которой равна Г = (D2+ 1)/(D3 + D2 + 1). Тогда

z = {D+\)x + EPz + Dh

Для получения нулевой последовательности положим 2 = 0 и решим уравнение

X = D4 + Dz + Dz

относительно х. Так как 2 = 0 для всей последовательности, то мы должны удовлетворить условию Dz = Dz = Dz = 0. Следовательно, для нулевой последовательности х = Dx. При начальных условиях Dx = Dx = Dx = I нулевая последовательность имеет вид 11... 1... .

Полином от Р степени k нельзя упростить, если его нельзя разложить на произведение полиномов степени, меньшей чем k. Если Г -передаточная функция неупрощаемого полинома степени й и не является множеством + 1, 2* - 1, то Г имеет циклическую нулевую последовательность периода 2 - S содержащую все подпоследовательностные длины k, кроме последовательности одних нулей. Такая последовательность называется нулевой последовательностью максимальной длины. Таблицы неупрощаемых полиномов, которые могут быть использованы для образования таких нулевых последовательностей, приведены во многих книгах по теории кодирования [16]. Такие полиномы играют важную роль при применении линейных цепей для исправления ошибок.

Применение линейных цепей для исправления ошибок

Простой пример применения линейных цепей для исправления ошибок приведен на рис. 3.48. Предположим, что сообщение М, состоящее из последовательности битов, кодируется путем

КоВирующее устройство

Канал с Щумвм

Декодирующее устройство

Рис. 3.48. Применение линейных цепей для исправления ошибок.

Пусть декодирующее устройство представляет собой другую линейную цепь с передаточной функцией Т~, где Г- - такая, что = = 1. Обозначив выход декодирующего

устройства через М*, получим

С = ТМ,

C = TM+N

М*= Т-С* = (ГУН -f Af) = -f r~iv.

Следовательно, чтобы правильно декодировать посланное сообщение, нужно путем наблюдения М* найти последовательность r-w.

Мы ограничимся случаем, когда шум приводит к ошибке в одном разряде, т. е. последовательность может содержать самое большее одну 1. Предположим, что М состоит из последовательности г информационных битов, за которыми следуют s нулей (М = rriimz ... tUrO ... 0). Если Af = 00 ... О, то М* = М и последние s разрядов М равны нулю. Чтобы найти из М* правильный выход, определим Т так, чтобы последовательность Af (и, следовательно, T-N) однозначно определялась из s последних разрядов М*. Можно показать [16], что если Т - неупрощае-мый полином степени k, то Г- имеет желаемое свойство, если 8 = киг = 2-1-к.

Пример 3.24. Т = D-\- D - неупрощаемый полином степени 3, Т- - 1/{D + D-\-I). Для исправления одной ошибки общее число разрядов в сообщении М должно быть равно 2 - 1 = 7. Сообщение М будет состоять из четырех информационных битов, за которыми следуют три нуля, т. е. М -

его подачи на вход линейной цепи с передаточной функцией Т. Выход этой цепи представляет собой закодированное сообщение С, которое затем передается по каналу с помехами. Принимаемое сообщение равно С* = С N, где Л^ -ошибки, вызванные наличием помех. Нужно спроектировать кодирующее и декодирующее устройства, такие, чтобы передаваемое сообщение однозначно определялось принимаемым сигналом С*.