шага 1 процедуры 3.5, а нижняя - с помощью шага 2 той же процедуры. Никаких других множеств состояний добавлять не надо, так как все элементы в таблице появились так же, как обозначения строк. Автомат является автоматом типа П относительно выхода Zi, поскольку необходимое условие было удовлетворено на всех шагах процедуры.

Учитывая, что автомат М4 относится к типу П, мы можем однозначно определить входную последовательность, соответствующую любому конечному состоянию и выходной последовательности. Например, выходная последовательность Zi 0000 и конечное состояние 3 формируются при входной последовательности 1110 и исходном состоянии 1 или 2, а выходная последовательность Zi 1100 и конечное состояние 3 - при входной последовательности ОНО и исходном состоянии 3 или 4.

Рассмотрим теперь процедуру идентификации обобщенного автомата без потери информации (тип III) и затем докажем ее справедливость.

Процедура 3.6. Тест для обобщенного автомата без потери информации

1. Построить тестовую таблицу, строки которой представляют отдельные состояния автомата М, а столбцы - множество возможных выходов М. Если текущее состояние равно Qi, а выход- Zj, то элемент в строке qi и столбце Zj характеризует множество возможных следующих состояний.

2. Добавить к тестовой таблице строки, соответствующие множествам состояний, которые явились элементами таблицы, если такие строки уже не существуют. Элемент в строке, соответствующий множеству состояний Qi и выходу z образует множество следующих состояний, если текущее состояние находится в Qi и выход равен г,. Процедура повторяется до тех пор, пока все новые строки не будут добавлены к таблице состояний.

3. Составить перечень множеств состояний М, которые содержат идентичные элементы следующее состояние - выход {N, Z). Если ни одно из состояний М не содержит два (или более) идентичных (Л', Z) -элементов и любое множество состояний М, которое не содержит идентичных (Л', Z)-элементов, не содержится в множестве состояний, полученных в результате шага 1 или 2, то автомат относится к типу III. В противном случае автомат не относится к рассматриваемому типу.

Пример 3.14. Таблица состояний автомата М5 и его тестовая таблица приведены на рис. 3.33. Элемент (3,1) появляется в множестве строк {2, 4}, элемент (4, 1)-в множестве строк {1, 4}. Так как ни одно из этих множеств не содержится в какой-либо строке тестовой таблицы, то автомат М5 относится

О

Рис. 3.33. Таблица состояний (а); тестовая таблица (б).

Рассмотрим декодирование выходной последовательности 00010, сформированной Ms при исходном состоянии 1 и конечном состоянии 2. Из тестовой таблицы следует, что состояние после первого выхода должно быть равно 3 (элемент в строке 1, столбце 2 = 0). Аналогично следующее состояние должно равняться 1 или 2 (элемент в строке 3, столбце 2 = 0). Следующие два состояния могут быть 3 или 4. Информация может быть представлена в виде

Выход: 0 0 0 1 0

Состояние: 1 3 12 34 34 2

Последний вход должен формировать выход О и следующее состояние 2 из состояния 3 или 4. Из таблицы состояний можно найти, что это произойдет только в том случае, если предыдущее состояние было 3 и вход х-1. Теперь последующий переход должен быть из состояния 3 или 4 к состоянию 3 с выходом 1. Из Ms можно сделать вывод, что вход должен быть равен О, а состояние соответственно 4. Продолжая рассуждения аналогичным образом, получим следующую входную последо-чательность: 01001,

К типу iii, т.е. является обобщенным автоматом без потери информации.

Так как автомат Ms относится к типу iii, то можно определить входную последовательность для любой выходной последовательности, обеспеченной известными исходными и конечными состояниями. Тестовая таблица также полезна для декодирования выходной последовательности (т. е. нахождения входной последовательности), возбужденной автоматом типа III для заданных исходного и конечного состояний.

2 3 4

Рис. 3 34. Таблица состояний (а); тестовая таблицу (б).

Лемма 3.11. Последовательностиыи автомат М является обобщенным автоматом без потери информации тогда и только тогда, когда ни одно из состояний не содержит двух или более идентичных элементов и в одном и том же множестве таблицы состояний не содержится двух состояний с одним и тем же (Л^, Z)-элементом (следующее состояние и выход).

Доказательство. Необходимость. Предположим, что (г, Zj) являются элементом следующее состояние - выход состояний Ча И qb, которые находятся в одной и той же тестовой таблице автомата М. Так как qa и qb находятся в одной и той же тестовой таблице, существуют исходное состояние qo и две входные последовательности Хо, Хь которые ведут к состояниям q и qb соответственно с той же самой выходной последовательностью Z. Следовательно, исходное состояние qo, конечное состояние qi и выходная последовательность Zzj не однозначно определяют

Пример 3.15. В таблице состояний Мб (рис. 3.34) элемент (2,0) появляется в множестве строк {1, 3}, а элемент (3, 0)- в множестве строк {1, 4}. Так как множество {1, 3} является строкой тестовой таблицы, то Me не относится к типу III. Выходная последовательность 00010 с исходным состоянием 1 и конечным состоянием 2 может быть образована входной последовательностью 00101 и 11000 и, следовательно, не может быть декодирована однозначно.

входную последовательность, и таблица состояний не является таблицей без потери информации.

Достаточность. Для любой выходной последовательности, заданной исходным состоянием и конечным состоянием, можно получить возможное множество состояний, которое образует каждый выход в выходной последовательности. Каждый из них соответствует множеству состояний в тестовой таблице. Пусть qj представляет собой конечное состояние, а Zi - последний выход последовательности. Тогда из таблицы состояний можно определить возможное множество последующих состояний.

Если условия леммы удовлетворяются, то в одном и том же множестве состояний тестовой таблицы не содержится двух состояний с элементом (г, Zi). Таким образом, последующее состояние, а следовательно и предшествующий вход могут быть определены однозначно. Эту процедуру можно повторять, пока входная последовательность не будет определена полностью.

Для выяснения свойств конечных автоматов без потери информации целесообразно построить импликационный граф автомата без потери информации, представляемого таблицей сос-стояний М. Граф содержит для каждой пары состояний {qi, qj) (qi может быть равно qj) узел, такой, что для некоторого состояния q и входов In, Im, Ih Ф Im N{q, Ih) = qj, N{q, Im = qi и Z(q,Ih)=Z{q,Im).Если граф содержит узел (9i, и N(qilh) = = qra, N{qj, Im) =9n и Z(qi, h) =Z{qj, Im) {In может быть равно h), то от узла {qi, qj) к узлу {qm, qn) проводится дуга.

Пример 3.16. Импликационный граф автомата без потери информации Ms, рассмотренного в примере 3.14, показан на рис. 3.35. Граф для таблицы M (рис. 3.36, а) приведен на рис. 3.36, б.

Лемма 3.12. Таблица представляет собой конечный автомат без потери информации степени k (тип IV) тогда и только тогда, когда ее импликационный граф не имеет циклов и узлов повторяющихся состояний {qj, qj), а самое длинное звено графа равно степени k (т. е. имеет k узлов и /г - 1 дугу).

Доказательство. Если импликационный граф автомата без потери информации содержит узел повторяющихся состояний {qj, qj), то существует исходное состояние qi и выходная последовательность Z, которая может быть сформирована двумя входными последовательностями Xi и Хг, что приводит к одному и тому же конечному состоянию qj. Если автомат находится в состоянии qi, входная последовательность XiX, и ХгХг-, где Xi - любая входная последовательность, формируют одну и ту же выходную последовательность. Следовательно, автомат не относится к типу IV для любого k. Если импликационный граф автомата без потери информации имеет цикл, то существует

Рис. 3.35. Импликационный граф Ms-

ф ©

а

Рис. 3.36. Таблица состояний (а); импликационный граф (б).

любого заданного исходного состояния и выходной последовательности длиной k + 1 эту выходную последовательность невозможно получить с помощью двух входных последовательностей, отличающихся первым входом. Таким образом, первый вход можно всегда определить по исходному состоянию и первым k-\-\ выходам; следовательно, автомат относится к типу IV и имеет порядок k.

Пример 3.17. Из импликационного графа Ms (рис. 3.35) следует, что автомат Ms является конечным автоматом без потери информации порядка 2, так как самое длинное звено имеет порядок 2. Декодирование выходной последовательности 001 при исходном состоянии 3 обнаруживает, что первый вход равен 1. Однако выходная последовательность 00 при исходном состоянии 3 может быть сформирована либо при входной последовательности 00, либо при 10. Из рис. 3.36,6 следует, что автомат M нельзя отнести к типу IV. Выходная последовательность 0111... при исходном состоянии 3 декодирована быть не может.

Интересно найти соотношение между различными типами автоматов без потери информации. По определению автомат типа I эквивалентен автомату типа IV степени О, автоматы типа I и II включают в себя автомат типа III. Таблица Mj

исходное состояние и произвольной длины выходная последовательность, которая может быть образована двумя или более входными последовательностями. Следовательно, автомат М не относится к типу IV. Если самое длинное звено импликационного графа имеет длину т> k, то существует исходное состояние и две различные входные последовательности длиной т-\-\, которые формируют одну и ту же выходную последовательность.

Достаточность. Если самое длинное звено импликационного графа автомата без потери информации имеет порядок fe, то для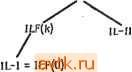

Рис. 3.37. Диаграмма соотношений между автоматами без потерь информации. GIL - обобщенный автомат без потери информации; ILF (k) - автомат без потери информации порядка k; IL-l - автомат без потери информации типа I; /L - II - автомат без потери информации типа II.

если автомат относится к типу I (или типу IV степени 0), то автомат типа IV степени к, который в свою очередь включает этот автомат, есть автомат типа III. Аналогично автомат типа II включает автомат типа III.

Для автомата М типа IV можно определить инверсный автомат М-, входы которого являются выходами автомата М. Если входная последовательность I, приложенная к М, дает на выходе последовательность Z, то М~* формирует выходную последовательность I с некоторым присущим ему запаздыванием, если к нему приложена входная последовательность (см. упражнение 3.24).

3.3.2. ЛИНЕЙНЫЕ ПОСЛЕДОВАТЕЛЬНОСТНЫЕ ЦЕПИ

Другим важным классом цепей являются линейные последовательностные цепи. Эти цепи имеют важное приложение для решения задач кодирования и декодирования данных. Сначала рассмотрим линейные комбинационные цепи, введенные в разд. 2.5.

Функция f(xi, Х2, Хп) называется лнейной, если она может быть представлена в виде

/ {хи Х2, л: ) Go Ф aiXi ф GaX, ф ... ф а^.

соответствует автомату типа I, но не типа II. Таблица Мг, наоборот, представляет собой автомат типа II, но не типа I. Следовательно, Б общем случае автоматы типа I и II несоизмеримы. Таблица Мб соответствует автомату типа III, но не типа II, а таблица М7 -автомату типа III, но не типа IV. Наконец, если таблица М -не автомат типа III, то существует некоторое состояние q и выходная последовательность Z, которые приводят к одному и тому же конечному состоянию для двух разных входных последовательностей, и, следовательно, М не является автоматом типа IV. Эти соотнощения между различными типами автоматов без потери информации можно представить диаграммой, приведенной на рис. 3.37, из которой следует, что

где aj==0,l, О J . Для изложения материала этого раздела удобно другое представление линейных функций. Говорят, что функция f{xi, Х2, .... Хп) линейнй, если она удовлетворяет принципу суперпозиции

f(aiXi, щх., a x ) = a,f (xi, О, О, О, ..., 0) + -

+ O.J (О, Х2, 0. О, ...) -f ... aJ (О, О, ..., О, Хп),

где аг, 1 t /г - константы. Для двоичного случая 1 = 0 или 1 и система счисления имеет модуль 2 (сумма четного числа единиц равна О, сумма нечетного числа единиц равна 1). Следовательно, для двоичных функций линейность включает

fiO, О, .... 0) = 0 и

f {Хи Х2.....х„)=f (X 0.....0) е / (0. Х2,0....) е

ef(0, о, О, Хп).

Если в первом определении Со = 1, то указанные определения могут оказаться несовместимыми. Эта кажущаяся несовместимость может быть разрешена путем выражения функции п переменных в первом определении в виде функции п + I переменных для применяемой суперпозиции. Пусть дополнительная переменная будет xq. Тогда

!(Хо, Хи х Xn) = fiXo, 0,0, 0)ef(0,x О, .... 0)0... е/(0. О, .... Хп),

где f{Xn, О, 0) = Оо (константа). (Заметим, что та же техника используется при анализе линейных систем других типов.) Следовательно, дополнение, по первому определению являющееся линейной функцией, так как х = I @ х, должно быть представлено как функция с двумя входами, а именно 1 и х, чтобы оказаться применимой при использовании принципа суперпозиции. Легко показать, что И и ИЛИ являются нелинейными функциями. Для И на два входа f{xu x2) = XiX2. Однако f{Xn,0)@f{0,X2) = 0®0 = 0¥=f{XuX2), так как Дх Х2)=1 для Xl = Х2 = I. Аналогично логический элемент ИЛИ является нелинейным элементом, так как f(xuX2)=Xi-\-X2, но f(0, Хг)© ®f{xuO)-= Х2®Х1фХ1 + хг.

Линейными являются только комбинационные функции, удовлетворяющие условию

f {Хи Х2, Хп) = aiXi ф OgX, ф ... фа х„,

где Xi = 0,l, 0</<

и Xj® Xi, = XjXk + XjXk.

6 Зак, 841

©

fj.lXf.X2- -Хп)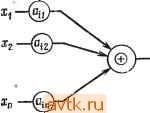

iiix.x. .х„)

= ai,x,@aizXz®-@ai x

Рис. 3.38. Представление линейных ко.мбинационных цепей.

У

©

Операция сложения по модулю 2 коммутативна и ассоциативна. Кроме того, /(х) ф /(Х) = О и Хг = 1 ф Хг.

Последовательностная цепь линейна, если выходная логика и комбинационная логика для функции следующего состояния, использующая D-триггер в качестве элементов памяти, линейны. Такая цепь изображена на рис. 3.39. В остальной части этого раздела мы будем использовать для представления сложения по модулю 2 символ -{- везде, где это не приведет к неправильному пониманию.

Линейная последовательностная цепь с п двоичными входами, k переменными состояния и т двоичными выходами может быть описана следующим множеством уравнений:

Yi = Z iiXj + Z аУ l<i<k,

2i = Z Уц>С1 + Z цУ1, \<i<,m.

Рис. 3.39. Представление линейной последовательностной цепи.

Таким образом, линейная комбинационная цепь может рассматриваться как цепь, составленная только из сумматоров по модулю 2 (рис. 3.38).

п п

/-=1 !>1

п к

Zi = Е yijXi + Е цУ1-/=1 /=1

Если определить оператор запаздывания D так, что Dx{t) = = x{t-\) и Dx{t) = x{t - k), то можно получить аналитическое выражение для выхода линейной последовательностной цепи без обратной связи. Легко показать, что такой оператор линеен. Так как yi = D(Yi), каждую переменную состояния можно выразить через сумму (по модулю 2) входных переменных Хг и входных псременных с запаздыванием DXi. Таким образом,

Используя матрицы-строки для представления входов, состояний и выходов, линейная последовательностная цепь может быть представлена в виде следующих матричных уравнений:

zT = Сх + DyT

где У = [Fl Уг, ..., У^], х = [х^х^, Хп], у = [t/it/s, , Ук1

Z = [2,22, . . . , 2 г], ЛГ - ТраНСПОЗИЦИЯ X,

А = [ац] представляет собой (k X п)-матрицу, В - [Pij] представляет собой {k X )-матрицу, С = [yij] представляет собой (т X п)-матрицу, D = представляет собой (т X )-матрицу.

Поведение линейных последовательностных цепей можно изучить с помощью линейной алгебры. Другим способом исследования таких цепей может служить техника передаточных функций, широко используемая для анализа линейных систем. Мы и воспользуемся этим способом.

Рассмотрим сначала линейные последовательностные цепи без обратных связей. Пусть цепь имеет п входов, k переменных состояния и т выходов. Поскольку в цепи нет обратной связи, переменные состояния могут быть выбраны таким образом, что любая переменная следующего состояния У будет зависеть только от входов и переменных состояния уг, j < i. Такая цепь описывается следующим множеством уравнений:

Ук = kiXi + а^2х2 -f ... + а^пХп = Е а^/Х/,

Рис. 3,40. Каноническая линейная последовательностная цепь без обратной

Передаточная функция Т = zjx, определяющая соотношение между выходом и входом как полином оператора D, имеет вид

Т = = ао + aD + а^ЕР -\- ... + at,D\

Вывод передаточной функции для цепи без обратной связи и синтез такой цепи по передаточной функции легко сделать путем сравнения цепи передаточной функции с каноническим представлением (рис. 3.40).

Рис. 3.41 Линейная последовательностная цепь к примеру 3.18 (а).

Пример 3.18. (а) Для цепи, показанной на рис. 3.41, 4 = = 2=1, аз = ао = 0. Следовательно, передаточная функция определяется выражением

TZaiDD-\-D\

все переменные могут быть представлены аналогичным образом. Для цепи, показанной на рис. 3.40, которая представляет собой в наиболее общем виде последовательностную цепь без обратных связей с одним входом и одним выходом,

z = aoX-\- у1 = аох + DYi = aoX + D {щх -f г/г) = ... == = UqX -f aiDx 4- CLzEx -f ... -f aDx.

Оператор D -линейный, поэтому выражения в нем можно делить, умножать и в общем совершать все операции в обычной манере, помня, что все суммы здесь по модулю 2.