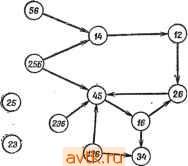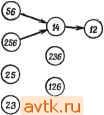Рис. 3.10. Импликационный граф ПС-множества (в); упрощенный.граф после исключения узла 45 (б); упрощенный граф после выбора узла 45 (в).

лучшего решения, содержащего узел Ni, целесообразно выбрать узел с большим коэффициентом разветвления по выходу. При этом узел Ni объединяет большое число узлов, которые нужно выбирать, и процедура поиска упрощается. Выбор узла Ni с большим коэффициентом объединения по входу позволяет исключить большое число узлов вместе с Ni на втором шаге процедуры. Для упрощения графов, полученных ветвлением, можно использовать концепции существенности и доминирования, аналогичные используемым при решении проблемы покрытия.

Пример 3.6. Импликационный граф таблицы состояний, приведенной на рис. 3.8, показан на рис. 3.10, а. Заметим, что 26 не является ПС-множеством, однако оно включено в импликационный граф, так как оно предопределяется ПС-множествами 12 и 16.

В результате ветвления вокруг узла 45, выполняемого при предположении, что 45 не является частью покрытия, узел 45 и все узлы, включающие 45, могут быть исключены, и граф примет вид, показанный на рис. 3.10,6. Он имеет только один узел.

полезной техника ветвления. Сначала выбирается узел Ni и определяется лучшее решение, содержащее Л^г и все узлы, включенные в Ni. Затем исключаются узел Ni и все узлы, которые прямо или косвенно включают Л^г, и находится лучшее решение, не содержащее Ni в результирующем графе. На каждом шаге для упрощения нахождения лучшего решения может понадобиться ветвление вокруг другого узла. Если любое решение, полученное в результате этой процедуры, удовлетворяет нижней границе, определяемой леммой 3.6, то решение является минимальным и процедуру можно закончить. Для упрощения поиска

покрывающий состояние 4, один узел, покрывающий состояние 5, и не имеет ни одного узла, покрывающего состояния 1 или 6. Поэтому 1, 6, 34 и 25 являются существенными и формируют замкнутое покрытие (1, 25, 34, 6), которое является минимальным покрытием, не содержащим 45.

Если предположить, что 45 является частью покрытия, то должны остаться узлы 16, 26 и 34, и граф принимает вид, приведенный на рис. 3.10, е. Так как 126 не включает на этом графе никаких узлов, а замкнутое покрытие должно содержать и 16 и 26, то оба этих узла можно заменить узлом 126. Получаемое при этом замкнутое покрытие (126, 34, 45) минимальное, поскольку существует несовместимое множество (135) трех состояний.

Иногда с помощью концепций замкнутости, доминирования и существенности импликационный граф можно упростить настолько, что ветвления не потребуется. Ниже эти концепции объясняются и иллюстрируются для графа, изображенного на рис. 3.10, а.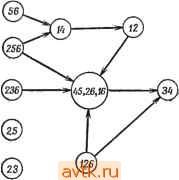

Рис. 3.11. Упрощенный ациклический импликационный граф.

1. Если на импликационном графе имеются направленные контуры, то условия замкнутости требуют, чтобы все ПС-множества, входящие в контур, были включены в покрывающее множество или ни одно из ПС-множеств не было включено в это множество. Это позволяет заменить все узлы контура одним узлом, характеризующим совместимые множества, представленные всеми узлами контура с весом, равным числу совместимых множеств. В результате получается ациклический граф. Узлы 16, 26 и 45 на рис. 3.10, с образуют замкнутый контур и могут быть заменены одним узлом с весом 3 (рис. 3.11).

2. Если от узла Ni к узлу Nj ведут два пути, один прямой, а другой косвенный, то прямой путь (ребро) от Ni к Nj может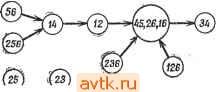

Рис 3.12. Импликационный граф после дальнейшего упрощения.

3. Рассмотрим два узла, обозначенных через Ni и Nj, где Nt и Nj представляют собой множества совместимых множеств. Узел Ni доминирует над Nj, если iVrjiVj, вес Ni меньше или равен весу Nj й Ni не содержит ни одного из узлов, не включенных в Nj. Если над Nj доминирует только один узел Ni, то Nj может быть исключен из графа, а все ребра, направленные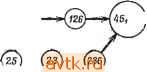

126>-

(23) (236)

Рис. 3.13. Импликационный граф после исключения доминирующего узла.

К Nj, заменены ребрами, направленными к Ni. Однако если над Nj доминируют два узла Л^г и Л^, то такую замену выполнить нельзя, если Nh не включает Ni. Применение этого правила к графу, изображенному на рис. 3.11, позволяет исключить узлы 56 (над которым доминирует 256) и 12 (над которым доминирует 126), как это видно из рис. 3.13.

Правило 3 также применимо к узлам, представляющим более чем одно совместимое множество (получено с помощью правила 1). Если некоторый узел доминирует над таким узлом, то последний может быть заменен доминирующим узлом. Узел 126 на рис. 3.13 доминирует над совместимыми множествами 16 и 26, поэтому они могут быть заменены узлом 126, приводя

быть исключен. (Заметим, что в результате применения упрощающего правила 1 узел Ni и/или Nj может представлять более чем одно совместимое множество.) Совместимые множества, представленные Ni, еще показаны как включающие узлы, представленные Nj, и выбор Ni требует выбора Nj. Применение этого правила к графу, изображенному на рис. 3.11, позволяет устранить ребра, связывающие узел 256 с суперузлом (с весом 3) и узел 126 с узлом 34. При этом граф приобретает вид, показанный на рис. 3.12.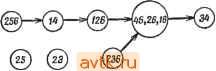

Рис. 3.14. Импликационный граф с упрощенным суперузлом.

Следуюш,ие ниже правила, основанные на импликациях внутри графа, определяют условия того, что данное совместимое множество представляет собой часть минимального замкнутого покрытия. (Заметим, что совместимые множества, не являющиеся ПС-множествами, могут сначала выбираться на основе импликаций внутри графа в качестве части минимального замкнутого покрытия с последующей заменой ПС-множествами, если они не дают минимального покрывающего множества.)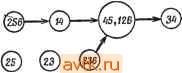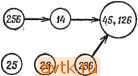

Рис. 3.15. Импликационный граф Рис. 3.16. Граф после выбора с исключенным узлом. узла 34.

(а) Пусть С есть множество совместимых множеств, выбранное как часть минимального покрывающего множества. Если qi - состояние, не содержащееся ни в одном из совместимых множеств, входящих в С, одно состояние qi не является ПС-множеством и все совместимые множества, содержащие qi, включают некоторый узел Ni, содержащий qi, то совместимое множество (множества), представленное узлом Ni, можно выбрать в качестве элемента минимального покрывающего множества. (Если Ni представляет совместимое множество, не являющееся ПС-множеством, или содержит такое совместимое множество, то он может быть последовательно заменен, если не является

К графу, изображенному на рис. 3.14. Вспомним, что первоначально узлы 45, 26 и 16 образовывали замкнутый контур. Следовательно, 126 не включает ни один из узлов, не включенных в 12 или 26.

4. Если Ni с: Nj и Ni включает Л',-, то Л^г может быть исключен, а ребра, направленные к Ni, направлены к Nj. Это правило позволяет исключить узел 126 из графа на рис. 3.14 и получить граф, изображенный на рис. 3.15.

частью минимального покрывающего множества.) Это позволяет исключить узел Л^, из графа, уничтожить все ветви, направленные к Ni, и включить в С все совместимые множества, представленные Ni. Если теперь С содержит два совместимых множества d. С такие, что Ci £ Cj, то исключить d из С.

Применение этого правила к состоянию 4 на рис. 3.15 позволяет выбрать в качестве части минимального покрывающего множества узел 34. При этом граф упрощается и принимает вид, изображенный на рис. 3.16.

Узлы (45, 126) на рис. 3.16 покрывают оставшиеся состояния и не включают ни один из других узлов. Общее число состояний, требуемое при таком выборе, равно 3, что соответствует нижней границе, определенной ранее для этой таблицы с помощью леммы 3.6. Следовательно, нет необходимости рассматривать для этого примера другие возможности и можно считать.

Рис. 3.17. Упрощенная таблица состояний.

ЧТО упрощенная таблица состояний получена (рис. 3.17). Вообще для нахождения минимального покрытия могут быть использованы и дополнительные правила.

(б) Пусть С - множество выбранных совместимых множеств. Если С не покрывает qt, то qi есть ПС-множество одного состояния и все совместимые множества, содержащие q включают Ni, содержащее qi, то Ni может быть выбрано, если Ni не включает ни один из других узлов, отсутствующих в С, и вес Ni равен 1. Это условие выполняется только в том случае, если Л^г в исходном СОСТОЯНИИ не включал других узлов, уже выбранных в качестве части минимального покрывающего множества.

Элементы, выбранные с помощью правил (а) и (б), могут не являться частью минимального замкнутого покрытия. В этом случае они заменяются с помощью правила (в).

(в) Если выполняются следующие условия: (1) некоторое заранее выбранное множество k совместимых множеств {kl) содержится в узле Nj с весом Np, (2) Л^,- не включает никаких других узлов и никакой другой узел Np не удовлетворяет условиям (1) и (2), то множество k совместимых множеств можно заменить совместимыми множествами, представленными Nj.

Это позволяет исключить Nj й все ребра, направленные к узлу Nj. Если некоторый узел Np также удовлетворяет этим условиям, то Nj не может быть выбран, кроме случая, когда N-p включает Nj.

Чтобы гарантировать невозможность дальнейшей замены узлов, нужно исключить все узлы графа, не входящие в искомое покрытие. Для этого используется следующее правило.

(г) Если С покрывает все состояния таблицы, узел Ni может быть исключен из графа при условии, что ни один из других узлов не включает Ni и в Ni содержится не более одного заранее выбранного совместимого множества. (Это правило необходимо для гарантии того, что временно выбранное совместимое множество будет заменено, если это приведет к более удачному решению.)

Несомненно, что легко сформулировать и другие правила упрощения графов, которые могут быть полезны в некоторых специфических случаях. Ниже мы продемонстрируем описанную выше графическую процедуру на дополнительном примере.

Пример- 3.7. Импликационный граф для таблицы, приведенной на рис. 3.18, изображен на рис. 3.19. Над совместимым множеством 12, включенным в ПС-множества 16 и 245, доминирует ПС-множество 125. Поэтому 12 может быть заменено на 125, 25 может быть исключен из графа, так как над ним доминирует 125. На основе правила (2) можно исключить ребро, направленное от 245 к 12. Узел 245 доминирует над 24, который с помощью правила (3) может быть исключен. В результате этих преобразований получается граф, представленный на рис. 3.20. Теперь с помощью правила (2) можно исключить ребро, направленное от 245 к 15 (показано на рис. 3.20 пунктиром). Далее, применение правила (а) позволяет выбрать следующие узлы для покрытия состояний: узел 15 для покрытия состояния 1, узел 45 для покрытия состояния 4, узел 46 для покрытия состояния 6 и узел 36 для покрытия состояния 3.

Отсюда следует, что С = {15, 45, 46, 36}. С помощью правила (в) узел 15 в С можно заменить на 125, а с помощью правила (г) узлы 245 и 16 можно исключить из графа. Тогда минимальное покрывающее множество имеет вид {125, 36, 46, 45}. (Заметим, что ни одно из максимальных совместимых множеств не содержит более трех состояний, откуда следует, что нижняя граница, определяемая леммой 3.6, не всегда может быть достигнута.) Упрощенная таблица состояний, определяемая этим покрывающим множеством, показана на рис. 3.21. Следует указать, что три следующих состояния имеют больше одного возможного значения, т.е. N{D, 01) =А или D (обозначено AjD), N(C, 11) = В/С и N{B, 10) ==C/D. Вообще совместимое множество Си может включать совместимое множество Сцг, такое.

Максимально совместимые Шо!Нетва:25,125,А6,16,ЗБ Шкштльио несовместимые множедтвц^З', 23,35,56,26

Рис. 3.18. Таблица состояний (а); диаграмма пар (б); перечень ПС-множеств (в).

ЧТО Сцг S Ср И Сц4 S Су. Если и Ср и Су находятся в покрывающем множестве, то следующее состояние, соответствующее Сцг, может быть либо Ср, либо Су.

Рассмотренные выше правила не всегда достаточны для получения минимального покрытия. Если из графа исключены все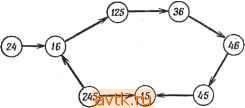

Рис. 3.19. Импликационный граф.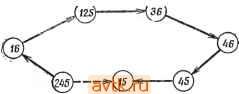

Рис. 3.20. Упрощенный импликационный граф.

ветви, то задача сводится к задаче нахождения минимального покрытия для таблицы простых импликант. (Покрытие выбирается среди узлов графа и отдельных состояний, являющихся

Рис. 2.21. Упрощенная таблица состояний.

ПС-множеством. Если контуры могут быть исключены из графа, то узлы могут иметь различные веса.) Эта проблема может быть-решена с помощью процедур, описанных в гл. 1, или сформулирована как задача целочисленного линейного программирования [3]. Если ребра остаются, но граф не может быть далее

3.2. ЭКСПЕРИМЕНТЫ

С ПОСЛЕДОВАТЕЛЬНОСТНЫМИ АВТОМАТАМИ

Прикладывая входные последовательности к последователь-постным автоматам и наблюдая выходные последовательности, можно получить информацию о начальном и конечном состояниях автомата и его таблице состояний. Входные и выходные

Исходное Выходная последовательность, состояние возбукдаетя входной последовательностью 111 А ООО

в 001

с 011

D 111

Рис. 3.22 Последовательностиыи авто.мат с диагностической последовательностью.

последовательности, используемые для анализа последовательностного автомата в указанной манере, называются тестами. Тесты полезны для определения реализации последовательностной цепью заданной таблицы состояний и применяются в диагностике неисправностей [5]. Ниже рассмотрим только основные принципы построения таких тестов.

Для таблицы М, приведенной на рис. 3.22, входная последовательность 111 образует различные выходные последовательности для каждого из четырех возможных начальных состояний. Поэтому применение этой входной последовательности к цепи, реализующей М, и наблюдение выходной последовательности служит экспериментом по определению начального состояния М. Р этом эксперименте приложенная входная последовательности

упрощен с помощью описанных выше правил, то, как показано выше, целесообразно использовать процедуру ветвления.

Если все неопределенные элементы в таблице состояний обусловлены определенными входными последовательностями, которые не могут произойти, то задача сокращения числа состояний может быть существенно упрощена [17]. В частности, если все неопределенные элементы обусловлены запрещенными входными последовательностями длиной 2, то каждое множество максимальных совместимых множеств, которое покрывает все состояния, является замкнутым. В этом случае процедура сокращения числа состояний сводится к задаче нахождения минимального покрытия максимальных совместимых множеств.

не зависит от наблюдаемой выходной последовательности. Такие эксперименты называются диагностическими.

В другом типе экспериментов мы сначала прикладываем вход (или входную последовательность) и наблюдаем выход. Последующие входы, приложенные к автомату, определяются наблюдаемыми значениями предыдущих выходов. Такие эксперименты называются наводяи^ими.

3.2.1. ДИАГНОСТИЧЕСКИЕ ПОСЛЕДОВАТЕЛЬНОСТИ

Эксперимент, с помощью которого находится начальное состояние автомата (как на рис. 3.22), называется диагностическим экспериментом, а используемая для этой цели входная последовательность - диагностической последовательностью. Предварительно заданные диагностические последовательности минимальной длины определяются с помощью диагностического дерева следующим образом.

Процедура 3.3. Диагностические последовательности

1. Диагностическое дерево имеет исходный узел (источник), соответствующий множеству Q всех (исходных) состояний автомата.

2. Для каждого входа h найти ветвь, соединяющую Q с узлом-преемником, представляющим множество всех следующих состояний, если исходное состояние находится в Q и приложен вход /ft. Группа этих состояний, соответствующая выходам Zi, связана с переходом к состояниям. Каждая такая группа соответствует возможным следующим состояниям, имеющим место после перехода из Q со входом h и выходом Zj.

3. Определить конечные узлы дерева, используя следующие правила:

(а) узел, в котором состояние появляется в группе более чем один раз, является конечным;

(б) узел, идентичный узлу более раннего уровня, является конечным;

(в) узел, в котором каждая группа представляет одно состояние, является конечным.

4. Если один или несколько узлов являются конечными по правилу (в) шага 3, то последовательность входов, соответствующая пути от исходного узла до такого конечного, является для автомата диагностической последовательностью. Если все узлы являются конечными по правилам (а) или (б), то автомат не имеет диагностической последовательности. Если дерево содержит несколько узлов, не являющихся конечными, то перейти к щагу 5.

5. Для каждого неконечного узла Qi и каждого входа построить ветвь, направленную от Qt к узлу-преемнику, пред-