вторяется до тех пор, пока существует возможность. Таким образом, все ячейки, несовместимых пар оказываются помечен-

4i Чг Чз Чп-г Чп-f

Рис. 3.5. Типичная диаграмма пар.

Рис. 3.6 Диаграмма пар для таблицы, изображенной на рис 3.1.

ными знаком X - Диаграмма пар, соответствующая таблице на рис. 3.1, приведена на рис. 3.6.

Определим теперь совместимые множества состояний, содержащие более двух элементов. Легко показать, что свойство со-

вместимости не транзитивно, т. е. если состояние qi совместимо с 9j (обозначается как qi ~ q и q ~ q), то из этого не следует, что qi ~ qk. Это иллюстрируется с помощью таблицы М на рис. 3.2, в которой I ~ 2, 2 ~ 3, но 1 3. Следовательно, нельзя находить совместимые множества объединением всех состояний, совместимых с одним и тем же состоянием. Однако для полностью определенной таблицы состояний свойство совместимости является транзитивным. Это существенно упрощает проблему нахождения совместимых множеств состояний.

Лемма 3.2. Если для полностью определенной таблицы состояний qi ~ qj и qj qm, то qt - q.

Доказательство. Предположим, что qtq qjq-m, а qi hqm-Тогда должна существовать входная последовательность I, которая, будучи приложенной к автомату в состояниях qi и q формирует полностью определенные выходные последовательности Zi и Z, причем Zi ф Zm. Если I, приложенная к автомату в состоянии qj, формирует выходную последовательность Zj, то по предположению Zj = Zj и Zj = Z, . Так как все выходные последовательности полностью определены, Zi = Zm, что противоречит предположению qijqm-

Вспомним, что для не полностью определенных таблиц состояний совместимость qt qj не предполагает, что выходные последовательности, образованные при начальных состояниях qi и qj, идентичны для любой входной последовательности, а означает только, что выходные последовательности одинаковы, если оба выхода определены. Следовательно, совместимость обладает свойством эквивалентности') только для полностью определенных таблиц состояний. Для таких таблиц совместимые множества состояний легко находятся с помощью свойства транзитивности. Необходимые и достаточные условия для нахождения совместимых множеств состояний не полностью определенных таблиц по совместимым парам состояний формулируются следующей леммой.

Лемма 3.3. Множество состояний Q = {д q, qn} таблицы состояний М совместимо тогда и только тогда, когда для каждой пары состояний [qi, qj) Q, qi ~ qj.

Доказательство. Предлагается выполнить в качестве упражнения.

Вообще таблица состояний может содержать большое число совместимых множеств состояний. Однако наибольший интерес представляет специальный класс таких множеств, не являющихся подмножеством ни одного из других совместимых множеств.

Этот класс множеств называется максимально совместимым (МС). МС-множество в таблице можно отыскивать с помощью диаграммы пар этой таблицы путем нахождения множеств состояний, удовлетворяющих лемме 3.3. Для этого используется следующая процедура.

Процедура 3.2. Пусть L = {Ci, Сг, ...} представляет собой множество, элементы которого являются совместимыми множествами состояний.

1. Найти самый правый столбец диаграммы пар, содержащий не менее одной пары совместимых состояний. Пусть этот столбец соответствует состоянию Qm- Поместить все совместимые пары этого столбца в множество L. (Это соответствует всем совместимым множествам вида {q-m, q], j > tn.)

2. Пусть k=m-\, a - мнол<ество всех состояний qj, j > k, совместимых с qi. Образовать множество = {cl \ cl = = (S;i П C() и {q для всех С,- g L}. Если для некоторого qt е Sk не существует множества С^, такого, что {q., q s С^, то включить {jqi, qk) в множество L (L - множество всех множеств совместимых состояний, содержащих q).

3. Заменить L на L U L. Если два множества С;, Су такие, что CiCj, то исключить Cl из L. (Теперь L соответствует

множеству всех совместимых подмножеств {q, Qk+u Qn}-)

4. Повторять шаги 2 и 3 для k = т - 2, т - 3, 1 (перемещаясь влево, пока не кончатся столбцы).

5. Прибавить к множеству L отдельные состояния, не содержащиеся ни в одном из множеств L. Тогда множество L будет содержать все МС-множества таблицы состояний.

Для удобства обозначения будем представлять совместимое множество состояний [qt, g,-, ..., qh] просто как qiqj, ..., q. Тогда множество совместимых множеств будет иметь вид [QiQj, -. , <?m, quqi, .., qm, ..}.

Пример 3.2. Анализ диаграммы пар на рис. 3.6 показывает, что самый правый столбец с совместимыми состояниями - это столбец 5 (5 6). Следовательно, первоначально L = {56}.

Перемещаясь влево, получаем S4 = 5 и S4 П 56 = 5, L = = {45}, а L = {45, 56}.

Аналогично 5з = 46 и

L = {(46 П 45) и 3, (46 П 56) и 3} = {34, 36}, L = {45, 56} и {34, 36} = {34, 36, 45, 56}. Для следующего (влево) столбца S2 = 356 L = {(356n34)U2, (356 П 36) и 2, (356 П 45) U 2, (356 П 56) U 2} =

= {23, 236, 25, 256}, L = {34, 36, 45, 56, 23, 236, 25, 256}.

Однако 36с=236, 23 с= 236, 25сг256, 56 с: 256. Вычеркнем множества, содержащиеся в других множествах:

L = {34, 45, 236, 256}.

Наконец, 5, =246 и U = {14, 14, 126, 126}. Вычисляя L [) L и исключая повторения, получим следующее множество МС-мно-жеств:

L = {14, 34, 45, 126, 236, 256).

3.1.2. ВЫБОР МИНИМАЛЬНОГО МНОЖЕСТВА СОВМЕСТИМЫХ МНОЖЕСТВ

При упрощении таблицы М до М' строки (состояния) М' должны соответствовать совместимым множествам состояний таблицы М. Если строка таблицы М' соответствует совместимому множеству Ci, то элемент в столбце /j таблицы М' должен соответствовать некоторому совместимому множеству С, , такому, что элементы следующего состояния в столбце Ij всех состояний в Сг должны содержаться в Ст-

Пусть Ci - множество совместимых состояний, а С - = = {QhlQk = !((1т, Ij) для всех Ci), т. е. Cij есть множество элементов следующих состояний для состояний множества Ci и входа Ij. Будем говорить, что множество Cij предопределяется множеством Ci. Множество совместимых множеств С = = {Си Cz, ...} является замкнутым, если для каждого С, е С все предопределенные множества Cij содержатся в некотором элементе из С для всех Ij. Множество совместимых множеств, соответствующих строкам (состояниям) таблицы М', должно быть замкнутым. Проблема минимизации числа состояний в таблице состояний М сводится к проблеме нахождения замкнутого множества С совместимых состояний минимальной кардинальности, которое покрывает каждое состояние из М, т. е. минимального замкнутого покрытия. Отметим, что множество всех МС-множеств замкнуто, но не обязательно обладает минимальной кардинальностью для произвольной таблицы состояний.

Лемма 3.4. МС-множества полностью определенной таблицы состояний непересекающиеся (т. е. для каждого состояния qi имеется только одно МС-множество, содержащее qi).

Доказательство. Предположим, что состояние qi содержится в двух МС-множествах Ci и Cg, Ci ф Cz. Так как Ci и Cg представляют собой МС-множества CxCz и Cz ф Cj. Следовательно, каждое из множеств С\ и Cz должно содержать некоторое состояние, не содержащееся в другом множестве. Пусть q е Ci, qiCz и quCz, но qkCi. Так как д,-, QjCi, то qtqj, а так как qi, q е Cz, то qi ~ q. Учитывая, что по предполо-

жению qj и q находятся в разных МС-множествах qj Ф q, что противоречит лемме 3.2.

Лемма 3.5. Множество всех МС-множеств полностью определенной таблицы является минимальным замкнутым покрытием.

Доказательство. Вытекает непосредственно из леммы 3.4.

Из лемм 3.4 и 3.5 следует, что полностью определенная таблица состояний М может быть минимизирована путем нахож-

(45) в

(6) с

-Рис. 3.7. Полностью определенный автомат (а); диаграмма пар (б); упрощенный автомат (в).

дения множества МС-множеств и образования таблицы М' с состоянием, соответствующим этим МС-множествам.

Пример 3.3. На рис. 3.7,6 показана диаграмма пар совместимости для таблицы состояний, приведенной на рис. 3.7, а. Множество МС-множеств {123, 45, 6}-замкнутое и минимальное, так как таблица полностью определена. Упрощенная таб* лица на рис. 3.7, е эквивалентна исходной таблице. Следующее

5 Зак, 841

состояние в столбце Ij для состояния, представляющего совместимое множество Cj, является состоянием, представляющим С,-,-, а выход равен выходу, ассоциированному с состояниями в Cj и столбце Ij исходной таблицы.

Так как лемма 3.5 несправедлива для не полностью определенных таблиц состояний, то желательно ограничить снизу число состояний таблицы, покрывающей данную таблицу. Такая граница может быть получена путем анализа множества несовместимых состояний. Несовместимым множеством состояний таблицы М называется множество состояний, не имеющее совместимых пар состояний. Несовместимое множество состояний, которое не содержится ни в каком другом несовместимом множестве состояний, называется максимально несовместимым множеством. Такое множество для таблицы состояний можно получить путем комбинации несовместимых пар состояний методом, полностью аналогичным процедуре 3.2.

Лемма 3.6. Если таблица М имеет максимальное несовместимое множество, включающее k состояний, то любая таблица, покрывающая М, содержит не менее k состояний

Доказательство. Каждое состояние максимального несовместимого множества должно быть покрыто отличным от других состоянием любой таблицы, покрывающей М, откуда и следует справедливость леммы.

Пример 3.4. Для таблицы состояний в примере 3.1 существуют следующие несовместимые пары состояний: (1,3), (2,4), (1,5), (3,5) и (4,6). Состояние 3 несовместимо с состояниями 1 и 5, и отсутствуют состояния, несовместимые с 1, 3 и 5. Следовательно, множество (1,3,5) является максимально несовместимым. Ни одну из оставшихся несовместимых пар объединить нельзя. Следовательно, максимально несовместимыми множествами являются: (1,3,5), (2,4) и (4,6). Любая таблица, покрывающая эту таблицу состояний, должна содержать не менее трех состояний, так как наибольшее из максимально несовместимых множеств имеет три состояния.

Проблема нахождения минимального замкнутого покрытия для не полностью определенной таблицы состояний намного сложнее, чем для полностью определенного случая. Это объясняется тем, что замкнутое покрытие, состоящее только из МС-множеств, может содержать больше множеств, чем замкнутое покрытие, в котором некоторые (или все) совместимые множества являются правильными подмножествами МС-множеств. Если в покрытии имеется МС-множество С, = {qu дг, 9з}> то необходимо, чтобы и следующие состояния, входящие в Сг, при

) Нижняя граница, определяемая этой леммой, достижима не всегда.

любых входах содержались в покрытии. Это может потребовать прибавления к покрытию совместимого множества, хотя необходимость в таком прибавлении для покрытия любого состояния отсутствует. Однако, если вместо МС-множества используется подмножество C=={gi, <?2}, то следующее состояние, входящее

в С'и уже может оказаться в выбранном совместимом множестве, что приводит к сокращению числа множеств в покрытии.

Из сказанного выще следует, что возможна ситуация, когда для получения минимального замкнутого покрытия не полностью определенной таблицы состояний нужно будет проанализировать все совместимые множества. Рассмотрим, однако, два совместимых множества Ci и С,-, таких, что Cj С,-. Если множества следующих состояний, входящих в Ci и Cj, для всех входов одинаковы, то, очевидно, нет необходимости для нахождения минимального замкнутого покрытия рассматривать множество С,-. Задача нахождения минимального замкнутого покрытия до некоторой степени упрощается при использовании концепции доминирующих совместимых множеств, позволяющей исключить некоторые совместимые множества из рассмотрения.

Пусть Сг - совместимое множество состояний, а Сг,- -множество следующих состояний, входящих в Сг, для входа /, (т. е. множество следующих состояний Сг для входа /, ). Класс множеств, предопределяемых С есть множество всех множеств Сц, входящих в Сг, ДЛЯ всех входов /,-, таких, что

1) Сг] содержит более одного элемента,

2) СцфСг,

3) Сц ф dk, если Cih е Pi.

Совместимое множество С, доминирует над совместимым множеством С,-, если Cj С, и s Pj, где Pi и Р,- представляют собой класс множеств, входящих соответственно в Ci и Cj. Если Сг доминирует над С,-, то Ci покрывает все состояния, покрытые Cj, и условия того, что покрытия, содержащие d или С,-, замкнуты, одинаковы. Таким образом, при определении минимального покрытия нет необходимости рассматривать множество С,-.

Совместимое множество состояний, не имеющее доминирующего над собой совместимого множества, называется простым совместимым множеством (ПС). Заметим, что единичное состояние Qi может представлять собой ПС-множество, если каждое совместимое множество d с более чем одним состоянием и содержащее qi, включает множество с более чем одним состоянием. Следующая ниже теорема демонстрирует полезность понятия ПС-множества для упрощения таблиц состояний.

Теорема 3.1. Для любой таблицы состояний М существует покрывающая М минимальная таблица М', все состояния которой соответствуют ПС-множествам таблицы М,

Доказательство. Предположим, что существует таблица М , представляющая собой таблицу с минимальным числом строк, покрывающую М, и что некоторая строка М соответствует совместимому множеству Cj, не являющемуся ПС-множеством.

Тогда существует ПС-множество С/, которое доминирует над Cj. Замена каждого элемента С, в М на С/ не приведет к увеличению числа состояний. Повторение такой замены для всех строк, соответствующих ПС-множествам, позволит получить результирующую таблицу состояний с числом состояний не большим, чем в таблице М .

Пример 3.5. Максимальные совместимые множества таблицы состояний, приведенной на рис. 3.8, а, диаграмма пар которой изображена на рис. 3.8,6, равны {126, 14, 236, 34, 45, 256}. Все МС-множества таблиц состояний являются также ПС-множествами. Остальные ПС-множества представляют собой подмножества МС-множеств, не имеющих над собой доминирующих МС-множеств или других ПС-множеств. Например, МС-множество 236 доминирует над совместимым множеством 26, так как класс множеств, входящий в оба эти множества, равен {45}. Полное множество ПС-множеств и включенных в них классов множеств приведены на рис. 3,8, в, где Pj = ф означает класс пустых множеств.

Следующим после определения ПС-множеств таблицы состояний шагом является получение множества минимальных покрытий ПС-множеств. Общая проблема может быть сформулирована как задача линейного целочисленного программирования [3], однако мы рассмотрим графическую процедуру, которую удобно использовать для относительно небольших таблиц состояний.

Во-первых, построим импликационный граф, изображающий ПС-множества и их импликации. Граф имеет узел Nu соответствующий каждому ПС-множеству Ci с более чем одним состоянием. Так как ПС-множества с одним состоянием могут включать только по одному состоянию (т.е. их классы множеств равны нулю), то нет необходимости включать их в явном виде в импликационный граф.

Если ПС-множество С, включает ПС-множество Cj, то ориентированное ребро графа идет от узла Ni, представляющего Ci, к узлу Nj, представляющему Cj. Если совместимое множество Cj, включенное в С,-, не является ПС-множеством, но над Cj доминирует только одно ПС-множество Си, то следует добавить ребро, идущее от узла Ni к узлу Л^. Если над Q доминирует несколько ПС-множеств, то следует добавить узел Nj, представляющий Cj, и ребро, идущее от Ni к Nj, понимая при этом.

Рис. 3.8. Не полностью определенный автомат (а); диаграмма пар (б); перечень

ПС-множеств (б).

г

3 h 5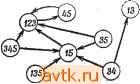

Piic. 3.9. Последовательностный автомат (в); импликационный граф ПС-множества (б); импликационный граф МС-множества (в).

{123, 15, 345, 34, 35, 45, 13}. Импликационный граф для этой таблицы показан на рис. 3.9,6. ПС-множество 15 включает 12, над которым доминирует ПС-множество 123. Это представлено ребром графа из узла 15 к узлу 123. ПС-множество 13 включает одно состояние 5 (т. е. относится к классу пустых множеств) и, следовательно, не имеет импликаций на графе.

Можно построить и упрощенный импликационный граф (рис. 3.9, е), все узлы которого соответствуют МС-множествам. Такой граф может быть использован для нахождения минимального замкнутого покрытия МС-множеств. (Поскольку для графа, изображенного на рис. 3.9, е, все узлы образуют цикл, это покрытие содержит все три МС-множества (123, 345, 15).) Если это решение согласуется с нижней границей, определяемой леммой 3.6, то оно является оптимальным. Однако в общем случае это неверно. Минимальное замкнутое покрытие таблицы, приведенной на рис. 3.9, с, (123, 45) вообще не содержит МС-множеств. В общем случае для получения минимальных замкнутых покрытий нужно использовать импликационный граф ПС-множеств, такой, как показан на рис. 3.9, б.

Для получения минимального замкнутого покрытия ПС-множеств с помощью импликационного графа часто оказывается

ЧТО далее такое совместимое множество можно будет заменить доминирующим над ним ПС-множеством.

Импликационный граф удобно использовать для получения минимальных замкнутых покрытий, так как он показывает все возможные импликации любого ПС-множества. Следовательно, если как часть покрытия выбирается узел Л^ то необходимо выбрать также и все узлы, включенные в Ni. Если Ni не выбирается, то узлы, включенные в Ni, не могут быть выбраны.

Множества МС- и ПС-множеств для таблицы состояний, приведенной на рис. 3.9, с, соответственно равны {123, 345, 15} и