БИБЛИОГРАФИЯ И КОММЕНТАРИИ

Задача минимизации многовыходовых комбинационных функций рассмотрена Мак-Класки и Шорром [9]. Материал по декомпозиции комбинационных функций впервые изложен Ашен-хурстом [1] и развит на случай не полностью определенных функций Хаитом [7].

Хорошим пособием для изучения этого материала является книга Куртиса [3]. Теория симметричных функций рассмотрена рядом исследователей, среди которых следует отметить Колдуэлла [2], Гаррисона [5] и Эпштейна [4]. Данные о юнатных функциях изложены Мак-Наутоиом [10], а о пороговых - Паулом и Мак-Класки [14]. Неразветвленные функции рассмотрены Хайе-сом [6]. Материал о логической полноте получен благодаря Посту [15] и обсуждался Мухопадхайя [11]. Опсал [13] рассмотрел задачу получения эффективных реализаций с помощью логически полных MHOHtecTB элементов.

ЛИТЕРАТУРА

1. Ashenhurst R. L., The Decomposition of Switching Functions, Ann. Computation Lab., Harvard University, vol. 29, pp. 74-116, 1959.

2. Cadwell S. H., Switching Circuits and Logical Design, J. Wiley and Sons, Inc., New Уотк, N. Y., 1958.

3. Curtis H. A-, A New Approach to the Design of Switching Circuits, D. Van Nostrand Co., Inc., Princeton. New Jercy, 1962.

4. Epstein G., Synthesis of Electronic Circuits for Symmetric Functions, IRE Trans. Electronic Computers, vol. EC-7, pp. 57-60, March 1958.

5. Harrison M. A., Introduction to Switching and Automata Theory, McGraw-Hill, Inc., New York, N. Y., 1965.

6. Hayes J. P., Minimization of Fanout in Switching Networlts, Proc. 15th Ann. Symp. on Switching and Automata Theory, pp. 133-139, New Orleans, La., October 1974.

7. Hight S. L., Complex Disjunctive Decomposition of Incompletely Specified Boolean Functions, IEEE Trans, on Computers, vol. C-22, pp. 103-110, January 1973.

8. Huffman D. A., Combinational Circuits with Feedback, Recent Developments in Switching Theory, A Mukhopadhyay (Ed.), Academic Press, New York, N. Y., pp. 2g-55, 1970.-

9. McCluskey E. J., Schorr H., Essential Multiple-Output Prime Implicants, Mathematical Theory of Automata, Proc. Polytechnic Institute Brooklyn Symposium, vol. 12, pp. 437-457, April 1962.

10. McNaughton R., Unate Truth Functions, IRE Trans, on Electronic Compu-. ters, voL EC-10, pp. 1-6, March 1961.

11. Mukhopadhyay A, Complete Sets of Logic Primitives, Recent Developments in Switching Theory, A Mukhopadhyay (Ed.), Academic Press, New York, N. Y.. pp. 1-26, 1970.

12. Muller D. E, Applications of Boolean Algebra to Switching Circuit Design

Е'гог Detection, IRE Trans. Electronic Computers, vol. EC-3, pp. 6-12,

13. Opsahl G. I., Optimum Logic Modules. IEEE Trans, on Computers, vol C-21, pp. 90-96, January 1972.

u}J- McCluskey, Boolean Functions Realizable with Single Threshold Devices, Proc. IRE, vol, 48, pp. 1335-1337, July 1960,

УПРАЖНЕНИЯ

2.1. Для каждого из нижеследующих множеств найдите минимальную двухступенчатую реализацию.

а) fl (xi, Х2, Хз) = Yi тс mj, тз, гае. f2 (xi, Х2, лга) = Y / 2, тз, mi, те;

б) fl (Хь Хъ Хз) = Ото, тз + Yj г. 7.

ие определено

f2 {Xi, Х2, Хз) = Y г. тз, т, + Y

не определено

в) fl (хи Х2, Хз, Xi) = Y тъ, тт, mi2, тп + /Лг.

це определено

f2(Xi. Х2, Хз, Х4) = 2]/Ло. ти /пг, тб+ Y

не определено

fs {х\, Х2, Хз, Xi) = Y ти /Иг, ms, m,2 -f Y is-

не определено

2.2. Цепь, изображенная на рис. 2.37, - минимальная двухступенчатая реализация множества функций {/ь/г}. где fi (Х], Х2, Хз, Xi) = Y то, т^+

+ Y Является ли функция /2(xi,X2,X3, 4) однозначно определен-

ие определено

ной? Докажите это или получите fa с максимальным числом неопределенных

элементов.

3

Рис. 2.37. К упражнению 2.2.

2.3. Для каждой из следующих функций найдите, если это возможно, декомпозиционную реализацию в определенной форме.

а) f(A;i. Х2, Хз, X4)=XlX2X3X4--XiX2X3X4--XiX2X4-fXlX2X4--X2X3X4 -f

+ Х1Х3Х4 в виде F {g (X Хз), Xs. х,);

б) f (х Х2. Хз, х4) = Х' о. тз, ms, те, т^, тю, mis, тп в виде F{g{xu

Х2), Хз, Х4);

в) f (хь Х2, Хз, Х4, Хз) = X1X2X4X5 -1- Х1Х3Х1Х5 -Ь Х1Х4 -1- Х2Ж3Х4 в виде F (g (xi, Х2, Хз), Xi, Xs), где g (xi, X2, хз)=Е' (g (X2, Хз), x,).

15. Post Е. L., Two-Valued Iterative Systems of Mathematical Logic, Annals of Mathematics Studies, vol. 5, Princeton University Press, Princeton, N. J., 1941.

16. Reed I. S., A Class of Multiple-Error-Correcting Codes and Decoding Scheme. IRE Trans Inform. Theory, vol. IT-4, pp. 38-49, 1954.

2.4. Для функции, заданной картой Карнау на рис. 2.38, определите значения элементов, обозначенных о, 6, с, которые необходимы для получения простой дизъюнктивной декомпозиции функции f в виде F{g(xu Х2), xs, Xt).

Рис. 2.38. К упражнению 2.4.

2.5. Какие из приведенных ниже функций симметричны?

а) /(xi, Х2, Хг, 4) = mi, Шг, т^, те, mj, т^, т , mis, тц-,

б) f {xi, Xo, Xs) = Y ти /712. mi, me, mr,

в) Hx\, X2, Xs) =Yjmi, mi, mj;

r) f{Xu X2, Xs, X4) = 2]mi, mt. me, m?, wig, тц, 114.

2.6. a) Если функции f](Xi, X2, x ) и f2{Xi, xj, .... Xn) симметричны, какое из приведенных выражений всегда симметрично и какое никогда?

f,-f2. fi+h, h®h-

б) Решить задачу а) прн условии, что fi - симметричная функция, а fi - несимметричная.

Рнс. 2.39. К упражнению 2.8.

в) решить задачу а) при условии, что ни fi, ни /2 не являются симметричными функциями.

2.7. При каких условиях функция f(x Х2, .... Хп) и функция, дуальная ей, являются симметричными?

2.8. Для функции /, заданной картой Карнау на рис. 2.39, определите элементы а, Ь, с так, чтобы / оказалась симметричной.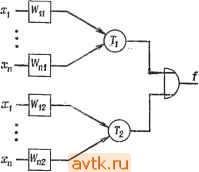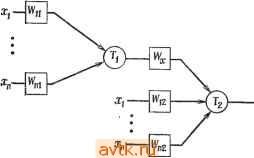

Рис. 2.40. К упражнению 2.9.

2.10. а) Докажите, что все простые импликанты полностью определенной юнатной функции существенны.

б) Является ли предыдущее утверждение верным для ие полностью опре-деленны.х юнатных функций?

2.11. а) Рассмотрите пороговую функцию f{xi, хо, х„) с весами то,-, i = 1, п и порогом Г. Если все веса равны, функция f называется мажоритарной функцией. Докажите, что все эти функции симметричны.

б) Все ли симметричные функции являются мажоритарными? Попробуйте наложить ограничения иа числа ki, йг, . . и т. д., чтобы функция Sk\, к2. hs-(Xi, Х2, ..., Хп) стала мажоритарной.

2.12. Функция f{xu Х2, .... Хп)-пороговая. Всегда ли является пороговой функция, дуальная f.

2.13. Какая из нижеследующих функций является пороговой, если /(хь Х2, Хг.) - пороговая функция и Xj, не является элементом множе-

2.9. Докажите, что цепи, изображенные на рнс. 2.40, а и б, могут быть использованы для реализации одной и той же функции при соответствующем выборе Wx, и найдите минимальное значение Wh, обеспечивающее решение поставленной задачи, как функцию Гь Гг, Шц, Wi2.

ства {xi, Х2, x }?

Xpf, Хр + f, Хр + f.

б) Решите задачу а) при условии, что Xj, - элемент множества [хи Хг, Хп].

2.14. Говорят, что функция /(х) дуально сравнима, если функция fd, дуальная f, такая, что f -\-fd = f или f + fu = fd.

а) Bee ли пороговые функции являются дуально сравнимыми?

б) Все ли дуально сравнимые функции являются пороговыми?

2.15. Сколько существует симметричных функций п переменных?

2.16. Сколько существует юиатных функции п переменных?

2.17. Пусть /(1, х,.....Хп)-булева функция, значения переменных которой равны либо О, либо 1, и существует множество весов даь Юг, - и) (Wi = +1 или -I, 1 г п) и действительное число Г, такое, что

п

f {Xj, 2.....п) Z1 ii

г = 1

и

п

f{l 2.....п) = 0 если Е ш.х,.<Г

Ясно, что Эта функция является специальным классом пороговых функций. Является ли эта функция полностью симметричной? Если является, то докажите это и укажите симметричные переменные и значение Т. Если не является, то приведите примеры нескольких таких функций, ие являющихся полностью симметричными.

2.18. Числа Фибоначчи представляют последовательность, определенную выражением

Рп = Fn-l + Fn-2,

где Fi - i-e число последовательности. Первыми членами последовательности

являются числа 1, 1, 2, 3, 5, 8.....

Рассмотрите множество функний

F = Xn+ Xn-i {Хп-2 + Хп-з (Xn-i + Хп-5 (- . - + Х2 (xi))) ...

(п -нечетное).

Покажите, что все функции этого множества являются пороговыми с весами Wn = Fn (я-е число Фибоначчи), и найдите значение порога Т.

Покажите, что это справедливо для функции, дуальной f, и найдите для иее значение Т.

2.19. а) Докажите для функции трех переменных f{Xi, хо, Хз), что если эта функция не является сохраняющей единицу, сохраняющей нуль и самодуальной, то она нелинейна.

б) Используя а), определите, сколько функций трех переменных fi таковые, что множество {/{} является сильно полным.

2.20. Для каждого из ниже следующих множеств функций трех переменных определите, является ли оно сильно полным, слабо полным, сильной базой или слабой базой.

а) /, = 2] иг тъ т^, т^,

б) {/l, Ы. где f2 = Yj 2-

в) {fu f2, fi}, где fs = Ото. тз, mi.

2.21. Спроектируйте модуль на четыре входа, реализующий функцию f(Xi, Xi, Xl) и удовлетворяющий следующим ограничениям:

1) /(О, Х2, Xs, Xi) = Х2 + Xs,

2) f(l, 0. 1, Xi) = Xi,

3) f{l, X2, 0, Xi) = X2,

4) fixu X2, 1, 0) = 1.

а) Является ли f слабо полной?

б) Является ли f сильно полной?

в) Если возможно, найдите функцию f, которая является сильно полной и удовлетворяет указанным ограничениям. Используйте эту функцию для реализации функции g = Х1Х2 + Х1Х2.

2.22. Множество функций {F} является сильно с-полным, если при использовании входов Xi и Xi могут быть реализованы все функции, и [Р] является слабо с-полным, если все функции могут быть реализованы с помощью входов Хг, Хг, О, 1. Найдите необходимые и достаточные условия сильной с-пол-ноты и слабой с-полноты.

Глава 3 ПОСЛЕДОВАТЕЛЬНОСТНЫЕ ЦЕПИ ИЗБРАННЫЕ ЗАДАЧИ

В гл. 1 мы рассматривали последовательностные автоматы в качестве моделей последовательностны.х цепей. В этой главе мы обсудим некоторые проблемы, связанные с анализом и синтезом последовательностных цепей, а также рассмотрим специальные классы последовательностных автоматов и цепей.

3.1. УПРОЩЕНИЕ ТАБЛИЦ СОСТОЯНИЙ

Первый шаг при проектировании последовательностной цепи по словесному описанию ее поведения заключается в получении таблицы состояний, описывающей поведение цепи. Такая таблица может содержать большее, чем необходимо, число состояний. Так как часто сложность проектируемой цепи зависит от числа состояний в таблице, число состояний желательно снизить.

Для данной таблицы состояний М нам бы хотелось получить таблицу состояний М' с меньшим числом состояний, такую, которая при соответствующих начальных состояниях для любой входной последовательности обеспечивала бы такую же выходную последовательность, как и таблица М. В качестве примера рассмотрим две таблицы состояний, показанных на рис. 3.1. Из таблицы М видно, что при начальных состояниях D или Е выходная последовательность остается одинаковой для всех входных последовательностей. Таким образом, выходная последовательность не меняется при любой входной последовательности, если все следующие состояния Е переходят в D. Более того, поскольку после такого изменения Е уже ие является элементом следующего состояния и выходные последовательности, возбужденные при начальном состоянии Е, идентичны последовательностям, возбужденным при начальном состоянии D для всех входных последовательностей, состояние Е может быть исключено, что приводит к уменьшению числа состояний и к таблице М'. Таким образом, число состояний М может быть уменьшено.

Если таблица состояний М определена не полностью, то достаточно потребовать, чтобы таблица М' обеспечивала те же, что и таблица М, выходные последовательности везде, где М определена. Состояние д' таблицы состояний М' покрывает состояние q таблицы М, если для любой входной последовательности выходные последовательности М' при начальном состоянии q и М при начальном состоянии q идентичны везде, где выходы М определены. Таблица М' покрывает таблицу М, если

м

Рис. 3.1. Два эквивалентных последовательностных автомата.

м

Рис. 3.2. Не полностью определенная таблица состояний и покрывающая

таблица.

Рис. 3,3. Полностью определенные таблицы, соответствующие таблице на

рис. 3.2, а.

каждое состояние М покрывается некоторым состоянием М'. Проблема упрощения (минимизации) таблицы состояний формулируется следующим образом: для данной таблицы М найти таблицу М', которая покрывает М так, что для любой другой таблицы М , покрывающей М, число состояний в М' не превышает числа состояний в М .

Для таблиц, приведенных на рис. 3.2, состояние А таблицы М' покрывает состояния 1 и 2 таблицы М, а состояние В таблицы М' - состояния 2 и 3 таблицы М. Следовательно, таблица М' покрывает таблицу М. Заметим, что при входной последовательности 100 и начальном состоянии 1 выходная последовательность равна О--. Таблица М' для начального состояния А

и той же входной последовательности обеспечивает получение другой выходной последовательности 001. Формируемые таблицей М' выходы, соответствующие неопределенным элементам таблицы М, не всегда одинаковы. Поэтому, если бы мы захотели получить таблицы Mz и путем заполнения неопределенных элементов М соответственно О и 1 (рис. 3.3), ни состояние Л, ни В таблицы М' не покрывало бы состояние 2 таблицы Мг или и как следствие М' не покрыла бы Мг или М3.

3.1.1. ПОЛУЧЕНИЕ СОВМЕСТИМЫХ МНОЖЕСТВ СОСТОЯНИЙ

Если таблица М может быть покрыта другой таблицей М' с меньшим, чем в таблице М, числом состояний, то некоторое состояние таблицы М' должно покрывать более одного состояния таблицы М. Если множество состояний таблицы М может [быть покрыто одним и тем же состоянием некоторой другой таблицы М', то это множество называется совместимым. Два состояния qi и qj таблицы М называются совместимыми, если они никогда не образуют различно определенных выходов для любой входной последовательности. Говорят, что два состояния и qj совместимы по выходу, если Z{qi, I) = Z{qi, 1) для всех h, для которых оба состояния определены. (Вспомним, что Ziqi, fk) есть выход, получаемый в том случае, когда к цепи, находящейся в состоянии д,-, прикладывается входной сигнал /).

Лемма 3.1. Два состояния д,- и qj таблицы состояний М несовместимы тогда и только тогда, когда и qj несовместимы по выходу или когда для некоторого h несовместимы N{qi, h) N(qj, h).

Доказательство. Необходимость. Предположим, что qi и qj совместимы по выходу и для всех 4 N{qi, lu) и N{qj, / ) совместимы. Если qi и qj несовместимы, то существует входная последовательность I, для которой они образуют различные выходные последовательности. Пусть I = /J (/1 перед Г). Так как qt и q совместимы по выходу, вход /ь приложенный к qi и qj, не при-

ведет к получению разных выходов. Следовательно, входная последовательность Г, приложенная к N(qi, /1) и N(qj, h), должна приводить к формированию разных выходов. Это противоречит предположению о том, что N{qi, 1) и N {q, Ih) совместимы для всех Ih.

Достаточность. Доказательство предлагается выполнить в качестве упражнения.

Для нахождения всех несовместимых пар состояний может быть использована следующая процедура. Процедура 3.1

1. Сформировать множество L, состоящее из всех несовместимых пар.

2. Прибавить к L любую пару состояний (qu qj), если для некоторого входа 4 пара {N{qi, Ih), N{qi, I и)) входит в L, т. е.

представляет собой предварительно найденную несовместимую пару состояний. Пара состояний [qi, qi) предопределяет пару состояний {N{qi, Ih), N{qj, h)).

3. Повторять шаг 2 до тех пор, пока существуют новые пары для внесения в L. Тогда L содержит все несовместимые пары состояний.

Пример 3.1. Используем процедуру 3.1 для нахождения множества несовместимых пар состояний для таблицы, изображенной на рис. 3.4.

Пары, несовместимые по выходу: {(1,3) (2,4)} = L=:5i. Новые пары, включающие Sr. {(1,5)} = S2. Новые пары, включающие S2: {(3,5), (4,6)} = 5з. Новые пары, включающие S3: нет.

Множество несовместимых пар: {(1, 3), (2, 4), (1, 5), (3, 5), (4,6)}.

Все остальные пары состояний совместимы.

Процедура нахождения совместимых пар для таблицы п состояний может быть выполнена в табличном виде с помощью диаграммы пар, имеющей вид, изображенный на рис. 3.5.

Заметим, что на диаграм.ме для каждой пары состояний (qu qj), i¥=j, предусмотрена своя ячейка. Если состояния qi и qj несовместимы по выходу, то в ячейку (qt, qj) заносится знак X - В противном случае ячейка заполняется всеми парами состояний, представляемыми (qi, qj). Если таких пар нет, то ячейка помечается меткой (V)- Пометим теперь знаком X все ячейки, содержащие пару состояний (qh, qi), если ячейка, соответствующая (qu, qi), помечена знаком X . Эта операция по-

Рис. 3.4. Не полностью определенный автомат.