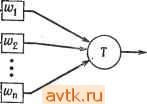Рис. 2.33. Представление порогового элемента.

При некоторых технологиях пороговые функции могут быть реализованы одним устройством, показанным на рис. 2.33 и называемым пороговым элементом. Пороговые функции интересны прежде всего именно с этой точки зрения.

Две следующие леммы показывают, что множество пороговых функций представляет собой собственное подмножество множества юнатных функций.

Лемма 2.8. Все пороговые функции юнатны.

Доказательство. Предположим, что функция f (xi, хг,..., х„) - пороговая с весами ш Шг, Шп. Если f не юнатна, то

Теорема 2.7. Полностью определенная функция f(xi, Х2, ... ..., Хп) юнатна тогда и только тогда, когда любое выражение суммы произведений этой функции содержит либо литерал хи либо JCi,-Ho не содержит одновременно оба этих литерала для всех Хи i = 1, 2, ..., п.

Доказательство. Предлагается выполнить в качестве упраис-нения.

Пример 2.15. Функция fi = XiXz-}- Х3Х4 юнатная. Функция же fa = X1X2XS -f Х2Х4 не юнатная, так как в минимальной сумме произведений одновременно содержатся Х2 и Х2.

Как следствие теоремы 2.7 юнатную функцию можно реализовать без использования инверторов, полагая, что в зависимости от того, является функция положительной или отрицательной относительно рассматриваемой переменной, имеется либо сама переменная, либо ее дополнение (но не обе вместе).

2.4.3. ПОРОГОВЫЕ ФУНКЦИИ

Функция f{xi, Х2, Хп) называется пороговой [14], если существует множество чисел {wi, W2, называемых ве-

сами, и число Т, называемое порогом, такие, что f(xi, хг, ...

п

Хп) = 1 тогда и только тогда, когда 2] ш^Х; Т, где Xj == О

или 1 и операции умножения и сложения арифметические (а не булевы).

существует выражение минимальной суммы произведений, в котором некоторые переменные Xi представляются как самой переменной, так и ее дополнением, и функция f может быть представлена в виде f == xtfaixi, Xz, ..., Xi-i, Xt+i, , + + Xifio{xi, X:, ...,Xi-i, Хг+ь .... x ), где fn ==f (xi, 2, ..., 1,

Xl + \, . , X ) и fio = f {Xl, Xz . Xi-\, 0, Xj + i, . . . ,

Если предположить, что Wi 0, то любая точка 1 функции fii есть также точка 1 функции fio. Следовательно, f = x,fio+fio и f отрицательна относительно Xi. Противоречие. Если же Wi О, то любая точка 1 f,o есть также 1-точка fii. Следовательно, f = Xifii -f fio и f положительна относительно Xj. Противоречие. Это доказывает, что не существует переменной Xi, такой, чтобы в выражении минимальной суммы произведений появились одновременно Хг и Хг. Таким образом, в соответствии с теоремой 2.5 функция юнатна.

Из доказательства леммы 2.8 следует, что если f - пороговая функция, то при Wi > О она положительна относительно Хг, а при Wi<.0 отрицательна относительно Xi.

Лемма 2.9. Не все юнатные функции являются пороговыми.

Доказательство. Рассмотрим юнатную функцию f = 1X2 -Ь -f Х3Х4 и предположим, что она является пороговой функцией с весами Шь шг, Шз и Ш4 и порогом Т. Так как f (1, 1, О, 0) =: 1, то Ш1 ~f 2 Г, и так как f (1, О, 1, 0) = О, то Wi-\-Wz<Z Т. Из этих неравенств следует, что w > w. Аналогично равенство f(0. О, 1, 1) = 1 предполагает, что Ш3 + Ш4 Г, а равенство f(0, 1, О, 1) = О, - что Шз > Ш2. Это противоречит предыдущему выводу (Ш2 <; Шз) и доказывает, что f не является пороговой функцией.

Для пороговой функции f(xi, Xz, Хп) 2 точек /г-куба с помощью гиперплоскости, определяемой уравнением Ш1Х1 ---f Ш2Х2 -f ... -f WnXn = Т, могут быть разделены на два непересекающихся множества: точек 1 и точек О, т. е. на одной стороне этой гиперплоскости располагаются точки 1, а на другой - точки 0.

Благодаря этому свойству пороговые функции также называют линейно-разделяемыми функциями.

Для каждой точки 1 функции fxj = (Xii, Xiz, ..., Xin) и для

каждой точки О этой функции Xj = (х^ь Xj2, Xjn),

п п

WkXik > Л wXjk- Следовательно, если f имеет 0-точку ко и fe=i fc=i

1-точку ki, то можно вывести ko-ki линейных ограничений (неравенств) на веса Wi, которые удовлетворяются только в том случае, если f является пороговой функцией. Однако одно из ограничений (Ci) может быть более существенным, чем другое

(Сг), в том смысле, что если Ci удовлетворяется, то Сг также удовлетворяется и, следовательно, Сг не требует подробного анализа.

Для юнатной функции f (xj, х^, x ) 1-точка является минимальной, если изменение любой положительной переменной от 1 до О или любой отрицательной переменной от О до I переводит х. в х'., где х^ - точки О функции f. Аналогично 0-точка X, функции f является максимальной, если изменение любой положительной переменной от О до 1 или любой отрицательной переменной от 1 до О переводит х^. в х^, где х^ - точка 1 функции f. Пусть ЛЬ - множество всех минимальных точек 1, а Мо - множество всех максимальных точек 0. Каждая пара элементов (pi, Pj), pi е Mi, р, е Мо определяет линейное неравенство переменных w. Если эти ограничения удовлетворяются, то ограничение, определенное любой точкой 1 и любой точкой О, также будет удовлетворяться. (Так как для любой 1-точки Xfe, если xMi, существует 1-точка е Mi, такая,

п п

что Yu gXkg > И gXig, ГДб Wg > О, бСЛИ f ПОЛОЖИТбЛЬНа ОТНО-<г=1 д-\

сительно Хд, и для любой 0-точки х„ ф Мо существует 0-точка

п п

X, еМо, такая, что Z дЛГт? < Z а^дЛГ/д, где ш,<0, если f от-

<7=1 <7=1

рицательна относительно л:.) Процедура 2.3

1. Для юнатной функции \{х\, х^, х„) определить множество Ml минимальных точек 1 и множество Мо минимальных

точек 0.

2. Каждая пара элементов (рг, Pj), РгМи р^еМо определяет линейное неравенство переменных ш. Если то и mi обозначают соответственно число элементов в Мо и Mi, то существует то-т\ неравенств. Решить, если возможно, эти неравенства, для того чтобы определить {wi, Шг.....Величину

п

порога найти из выражения Г = min Х 1Хц, где р^ =

= \Хп, Xi2, Xin).

Доказательство леммы 2.9 иллюстрирует применение процедуры 2.3 для того, чтобы показать, что данная функция не является пороговой. Если все ограничения удовлетворяются несколькими переменными Wi и Т, то функция является пороговой, так как при этих значениях Wi н Т для точек О, не смежных с гиперплоскостью, справедливо неравенство^ШгХг < Г, а для точек 1, не смежных с гиперплоскостью, справедливо неравенство WiXi > Т.

Пример 2.16. Рассмотрим юнатную функцию

f (хи Xz, Хз, Xi) = + 3 + Х1Х4.

Точка 1 (0,1,1,0) является минимальной, поскольку изменение Xz до О приведет к f - 0. Аналогично изменение Хз до 1 переведет точку 1 (О, О, О, 0) в точку 0. Продолжая эти рассуждения, получим следующие множества минимальных точек 1 (Mi) и максимальных точек О (Мо):

Mi = {(0, 1, 1, 0), (О, О, О, 0), (1, О, 1, 1,)}, Л1о = {(0, О, 1, 1), (1,0, 1,0)}.

Из этих множеств получим следующие множества ограничений:

Wz + Шз> W3 + Wi, (1)

W2+W3>Wi + W3, (2)

0>W3 + Wi, (3)

О > Ш1 -f W3, (4)

Wi-\- Wi-\- Wi> W3 + Wi, (5)

Wi-\-Wi + Wi> Wi + Щ- (6)

Ограничение (5) подразумевает Wi > 0. Для удовлетворения этого ограничения положим Wi = Для удовлетворения ограничения (4) положим Шз = -2. Чтобы удовлетворить ограничения (6) и (3), выберем 12)4=1, а чтобы удовлетворить ограничения (2) и (1), выберем Wz - 2. Величина Т находится из элементов Mj:

Wz+W3T, (7)

0>Т, (8)

Wi-\-W3 +WiT. (9)

Значение Г = О удовлетворяет все эти неравенства для (wu Wz, Шз, Ш4) = (1, 2, -2, 1).

Когда число переменных функции возрастает, множество не-линейностей может оказаться слишком большим для решения вручную, как это было сделано в рассмотренном примере. В этом случае может быть использована техника линейного программирования.

Специальные классы функций и их свойства, представляющие интерес, меняются с изменением технологии. Другим важным свойством, зависящим от технологии, является количество разветвлений по выходу, необходимых для реализации функции.

Как мы увидим ниже, наличие разветвлений по выходу вносит трудности при использовании логики на магнитных доменах. Следует отметить, что степень трудности проверки цепи зависит от общего количества разветвлений по выходу в ней. По этой причине желательно реализовать функцию цепью с минимальным количеством разветвлений по выходу. В цепи без разветвлений по выходу каждый вход и выход каждого логического элемента является входом не более одного логического элемента. Хайес [6] показал, что класс функций без разветвления по выходу (т. е. функций, которые могут быть реализованы цепями без разветвлений по выходу) является подмножеством юнатных функций, и разработал простой тест для определения, является ли юнатная функция неразветвленной по выходу. Более общая задача определения минимальных с точки зрения разветвлений по выходу реализаций произвольных функций не решена.

2.5. ПОЛНЫЕ МНОЖЕСТВА

ПРОСТЫХ ЛОГИЧЕСКИХ ФУНКЦИЙ

Комбинационная цепь может рассматриваться как соединение простейших одновыходных комбинационных цепей, называемых простыми логическими элементами., которые реализуют простые логические функции [11]. Например, реализацию функции в виде суммы произведений можно трактовать как соединение простых логических элементов И, ИЛИ и НЕ. Несмотря на то что комбинационные функции могут быть реализованы цепями с обратными связями [8], мы рассмотрим только реализации без обратных связей. Основной вопрос формулируется так: дано множество простых логических элементов; можно ли путем надлежащего их соединения реализовать произвольную комбинационную функцию? Множество простых логических функций, которые можно использовать для реализации любой комбинационной функции, называется логически полным.

Множество логических элементов называется сильно полным, если любая произвольная комбинационная функция, включая постоянные О и 1, может быть реализована путем соединения конечного числа элементов из этого множества при предположении, что в качестве входов рассматриваются входные переменные [xi, ..., л: ) без их дополнений. Множество логических элементов, достаточное для реализации всех комбинационных функций при входных переменных, включающих (хь... ,x ), а также О и 1 и не включающих хи Хп, называется слабо полным ).

) Можно также определить сильно с-полные и слабо с-полные множества функций, в которых присутствуют как входные переменные, так и их дополнения (см. задачу: 2.22).

Любая комбинационная функция может быть реализована в виде суммы произведений на базе логических элементов ИЛИ на два входа, И на два входа и НЕ, которые образуют сильно полное множество простых логических функций. Логический элемент И может быть реализован с помощью элементов ИЛИ и НЕ, которые формируют сильно полное множество. Аналогичным образом, логические элементы И и НЕ также образуют сильно полное множество. Логические элементы НЕ-И сами по себе образуют сильно полное множество, так как с их помощью реализуются функции ИЛИ (и И) и НЕ. Функции Исключающее ИЛИ и И вместе образуют слабо полное множество, поскольку хотя элемент НЕ и может быть реализован как х = = 1 ф л:, но постоянная 1 не может быть реализована. В зависимости от того, позволяет или нет множество логических элементов реализовать функции ИЛИ (или И) и НЕ, оно соответственно будет полным или неполным. Однако это трудно определить, кроме тех случаев, когда элементы имеют только небольшое число входов. Поэтому желательно определить полноту множества логических элементов, учитывая свойства функций, входящих в множество. При этом полезны следующие свойства комбинационных функций:

1. Сохранение нуля. Функция f(xi, Xz, x ) называется сохраняющей нуль, если f (О, О, ..., 0) - 0.

2. Сохранение единицы. Функция f (л: xz, . .., х„) называется сохраняющей единицу, если f(l, 1, 1) - 1.

3. Самодуальность. Функияя fd,дуальная функции f{xi,x2,... Хп), была определена в гл. 1 следующим образом:

fd{Xi, Xz, Хп) = f{Xu Xz, Хп). функция f(Xu Xz, Хп)

называется самодуальной, если fd{xu xz.....Хп) =f(xi, Xz, ...

. . . , Х-п) .

4. Положительная юнатность (монотонность) была определена в разд. 2.3 и может быть сформулирована следующим образом: пусть а = (аи az, ..., с„) и b = (bi, bz, ..., bn) - любые две точки в п-кубе. Тогда f{xu Xz, ..., Хп) положительно юнатна только в том случае, если f(a) f(b) для всех а Ъ. Напомним, что а Ь, только если Cj для всех i, 1 i и.

5. Линейность. Говорят, что функция f(xi, Xz, Хп) линейна, если она может быть представлена в виде f(xu Xz, ...

Хп) =aoQ aixi 0 azXz 0 ... 0 a.nX. , где ai = 0,1 для i = = 0, 1, 2, ..., п.

Лемма 2.10. Пусть F = {fi, fa, ..., f} представляет собой множество элементов, каждый из которых обладает любым, но одним и тем же свойством Р из перечисленных выше пяти свойств. Любая комбинационная функция, реализованная комбинацией элементов этого множества, также обладает свойством Р.

Доказательство. Докажем лемму только для свойства линейности. Ее доказательство для других свойств аналогично.

Без потери общности рассмотрим цепь, изображенную на рис. 2.34, где fi, fft и g являются линейными функциями своих входов и Xij{xi, Х2, х }. Если эта цепь реализует f (xi, Х2, .. ., Хп), то z = f (Xi, Х2, ..., х„) = g (Xi, ..., x , fi(xib ip), h{4u Xkq)). Так как g есть линейная функция, z = ао® aifi (хц, ..., xip)0 ... ®а^и {Xku . W ®

I, X,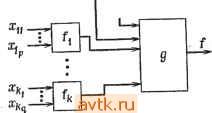

Рис. 2.34. Основная цепь с модулями для реализации линейных функций.

©biXi® ... фЬетХ„. Поскольку каждая функция fi также линейна, z = ao©ai (cio©c x 0 ... ©CipXjp)© ... фс (с^-f + CftiXfei© ... ©CfefXfe,)©biXi© ... ФЬ Х; . Постоянные а^, bi и сц равны либо О, либо 1. Следовательно, выход цепи можно выразить в виде z = do®diXy@ ... @dnXn, где (ii = 0,l. Заменяя линейными функциями любое число входов цепи, можно показать, что выход также является линейной функцией. Таким образом, лемма 2.10 справедлива для любой ациклической цепи линейных функций.

Лемма 2.11. Если входами являются постоянные О и 1, то операция НЕ может быть реализована любой функцией, которая не является положительно юнатной.

Доказательство. Пусть функция f (xi, Хг, ..., Хп) не является положительно юнатной. Это предполагает, что существуют некоторые а= (ai, С2, а„) и Ь = (bi, Ьг, Ьп), такие, что а > Ь, но f (а) = О и f (Ь) = 1. Пусть X есть множество входных переменных, имеющих значение 1 в а и О в Ь. Так как а > Ь, содержит по меньшей мере один элемент и все переменные х, ф. фХ имеют одинаковые значения как в а, так и в Ь. Дополнительный у вход может быть реализован путем соединения входа У со всеми Хг е Z и принятия Xj = aj 1= bj для всех Xj ф X.

Лемма 2.12. Если входами являются постоянные О и 1, то операции И и ИЛИ могут быть реализованы любой нелинейной функцией.

Доказательство. Любая комбинационная функция может быть выражена суммой минтермов. Так как каждый момент времени не больше чем 1 минтерм может равняться 1, логическая сумма может быть заменена элементами Исключающее ИЛИ. Заменяя канадую дополнительную переменную Xj в каждом терме величиной 1 ф и упрощая термы, получим представление функции в виде о + Х а^ХцХ^, Xju, где {Xji, Xj2, Xjk) есть подмножество переменных Хи Xj, х„, Сг = 0,1, а Х-сумма по модулю 2 (см. задачу 1.11). Такое представление называется разложением Рида-Мюллера [12, 16].

Если функция линейна, то каждое не равное нулю терм-произведение в этом разложении содержит только одну переменную Хг.

Если f{xi, Х2, ..., Хп) нелинейна, то в ее разложении должен находиться хотя бы один терм, содержащий две или более переменных. Пусть один такой терм имеет вид pXiXj, где р может быть I или произведением других переменных. Выберем терм с наименьшим числом переменных и установим значения всех переменных, содержащихся в р, равными 1. Переменным, отличающимся от Хг, Xj, и переменным, содержащимся в р, дадим значения 0. Обозначим полученную таким образом функцию через h (х Xj) = Со ф а^Хг ф azXj ф xXj. При Со = = сг = О h{Xi, Xj) = XiXj, а при Со = О, Ci = аг = 1 h{Xi, Xj) - Xi + Xj. Остальные шесть комбинаций Со, ai и сг дают следующие значения функций: XiXj, XiXj, Xi + Xj, Xj + Xj, Xi + Xj и XiXj. Ни одно из этих шести значений не является положительно юнатной функцией. Если Со, ai и Сг принимают одно из этих шести комбинаций значение, то лемма 2.12 может быть использована для формирования функций НЕ, которые в свою очередь могут быть использованы для образования дополнительных входов или выходов, необходимых для реализации функций И или ИЛИ (с помощью законов Де Моргана).

Теорема 2.8. Множество логических элементов называется слабо полным в том и только в том случае, если оно содержит по меньшей мере одну функцию, которая не является положительно юнатной, и по меньшей мере одну нелинейную функцию.

Доказательство. Необходимость условий следует из леммы 2.10, а достаточность - из лемм 2.11 и 2.12. Следует отметить, что постоянные О и 1 соответственно не являются сохраняющими О и 1 и самодуальными.

Пример 2.17. Пусть f(Xi, Xj, Xg, х4)= I ф XiXgXg ф X2X3.V4.

Используя конструкцию доказательства леммы 2.12, получим f{Xi, Х2, 1, 0) = /г{Х1, Х2)== 1 ф Х1Х2 = Х] + Х2. Так как функция Л(х1, Хг) не является положительно юнатной, ее можно использовать для реализации НЕ, полагая xi или Хг равной 1. На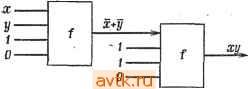

Рис. 2.35. Реализация произведения х - у сложным модулем.

Необходимо рассмотреть два случая: (1) функцию fi, которая не является сохраняющей нуль, а является сохраняющей единицу, и (2) функцию f% не сохраняющую ни нуль, ни единицу. в случае (1) постоянная I реализуется подсоединением всех входных зажимов f к той же переменной. Аналогично постоянная О получается при подсоединении всех входов к той же переменной.

В случае (2) fi(0. О, .... 0)= I и /i(l, 1, 1)= 0. Присоединяя все входные зажимы этого элемента к той же входной переменной, мы можем реализовать функцию НЕ. Теперь любую несамодуальную функцию fz (которая может быть той же функцией, что используется для реализации НЕ) можно использовать для реализации постоянных О и 1 следующим образом: так как fz не является самодуальной, то существует некоторая входная комбинация (сь az, й„), такая, что fz{a\, az, о! ) = = /2(01, 0,2, йп), где Сг = О, 1, 1 i п. Без потери общности положим, что Gj = о для 1 r А и Ui - I для ft + 1 i r. Постоянные О и 1 могут быть получены с помощью функции НЕ (реализованной как описано выше) и иесамодуаль-ной функции fz, как показано на рис. 2.36. Постоянные О и 1 формируются на выходах А и В, однако, на каком из них будет О, а на каком 1, зависит от функции fz. Если /2(01, G2,..., п) = = О (1), то Л = 1 (0) и В = О (1).

рис. 2.35 показана реализация произведения х-у с помощью модуля с выходом f = 1 ф XiXiXz ф Х^ХйХц.

Теорема 2.9. (Теорема Поста [15].) Мнон<:ество логических элементов {F} является сильно полным в том и только в том случае, если {F} содержит функцию, которая не является 1) сохраняющей нуль, 2) сохраняющей единицу, 3) самодуальной, 4) положительно юнатной и 5) линейной. (Каждому из этих свойств может соответствовать своя функция в /.)

Доказательство. Необходимые условия вытека.ют из леммы 2.10. Достаточность доказывается тем, что реализуются постоянные О и 1 и затем применяется теорема 2.8.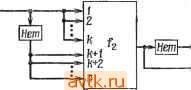

Рис. 2.36. Реализация постоянных О и 1.

Доказательство. Сильная база должна удовлетворять условиям теоремы 2.9. Однако функция, которая не сохраняет нуль, также не является ни сохраняющей единицу, ни самодуальной (доказательство предлагается выполнить самостоятельно). Таким образом, максимальное число элементов в сильной базе равно четырем. В силу того что существуют неотрицательные функции, которые также являются положительно юнатными (т.е. И), из теоремы 2.8 следует, что максимальное число элементов в слабой базе равно двум.

Интересно рассмотреть относительную эффективность различных логически полных множеств элементов при реализации произвольных функций. Наиболее сложным представляется использование модуля с выходом f для реализации --функции, дуальной /.

Для реализации операции НЕ на три входа необходимо пять логических элементов НЕ-И. Поэтому вполне вероятно, что множества элементов, содержащих дуальные пары, могут оказаться относительно эффективными, а полное множество {НЕ-И, И) менее эффективно, чем {НЕ-И, НЕ). Однако эта гипотеза не была проверена и в отношении измерения эффективности или получения эффективных реализаций с помощью полных множеств элементов также сделано мало [13].

После получения одним из описанных выше способов постоянных О и 1 функции ИЛИ и И могут быть реализованы с помощью нелинейной функции, как это следует из доказательства леммы 2.12. Функция НЕ реализуется с помощью юнатной функции, не являющейся положительно юнатной, и постоянных О и 1, как следует из доказательства леммы 2.11.

Сильно (слабо) полное множество логических элементов называется сильной (слабой) базой, если несобственное множество логических элементов также является полным.

Теорема 2.10. Максимальное число логических элементов в сильной базе равно четырем, а в слабой базе равно двум.