серии импульсов как время между двумя последовательными прохождениями импульса через заданную точку z, например Z = 0,5. Значения v к Т для волны, изображенной на рис. 6.19, указаны в подписи к рисунку (они были найдены вычислениями из результатов динамического моделирования). При более высоких значениях Хр волны уже не возникают и система стабилизируется на устойчивом неоднородном стационарном решении. Более подробные результаты можно найти, например, в работе [6.31].

6.5.2.2. Волна типа фронта

Фронт представляет собой переход решения системы типа реакция - диффузия от одного устойчивого стационарного решения к другому, причем в переходном режиме одна часть системы характеризуется значениями одного решения, а другая- значениями другого решения. Между этими двумя частями располагается узкая область (фронт), где наблюдается резкая зависимость физических переменных задачи от пространственной координаты. Указанный фронт перемещается, в результате чего размеры обеих областей изменяются до тех пор, пока система не достигнет конечного стационарного состояния, и фронт исчезнет.

Волну типа фронта мы снова продемонстрируем на примере задачи 12 при значениях параметров уз = 3, vo = 0,01, р = 1,5, 6=1,7, а =12. Стационарные решения системы (Р4-1), (Р4-2) в данном случае имеют вид:

S,: a;i = 0,12985, г/, = 0,12404 (устойчивый узел);

Sg: д;2 = 0,26666, г/г = 0,27906 (седло);

S3: 1,32824, г/з = 5,33927 (устойчивый фокус).

Если для распределенной системы (4.3.7) выбрать граничные условия второго рода, т. е. условия (4.3.12), то тривиальные стационарные решения

x{z)xu y(z)yu (6.5.8)

x{z)x, y{z)ys (6.5.9)

оказываются устойчивыми при Dx = 0,008, Dy = 0,004, L = 2,5, причем от начальных условий зависит, на каком из этих решений система стабилизируется.

Переход системы из состояния (6.5.8) в состояние (6.5.9) моделировался путем изменения начального условия для переменных X и у в точке г = 0 в течение промежутка времени ij:

f[0,fi]:x{0,t) = X3, y{0,t) = ys. (6.5.10)

Для моментов времени t > t\ вновь действуют граничные условия второго рода. Состояние системы (в некоторый момент времени) для ti - Q,\ показано на рис. 6.20. Скорость движения фронта при этом составляла и-~ 0,115; весь переход от (6.5.8) к (6.5.9) продолжался приблизительно 22 временных единицы. При очень малых значениях t\ система возвращается к стационарному решению (6.5.8). Более подробно эти результаты обсуждаются в работе [6.31]. Отметим также, что

Рис. 6.20. Волна типа фронта для задачи 12 при ГУ2: у = 3, Vo = 0,01, Р = = 1,5, 6 = 1,7, а = 12, Dx = 0,008, Dy = 0,004, L = 2,5; штриховая линия - решение (6.5 8), штрихпуиктириая - решение (6.5.9).

переходы из одного стационарного состояния в другое могут происходить либо легко (под влиянием малого возмущения, действующего в течение короткого времени), либо с трудом, если на границе системы вообще не реализуемы физически допустимые возмущения.

6.6. КВАЗИСТАЦИОНАРНОЕ ПОВЕДЕНИЕ РАСПРЕДЕЛЕННЫХ СИСТЕМ

Понятие квазистационарного поведения было введено в § 5.10. В этом параграфе мы рассмотрим лишь два типичных примера такого поведения для задач 11 и 13.

Прежде всего мы исследуем эволюцию стационарных структур в задаче 13 при предписанном изменении (увеличении со временем) длины системы L. Эволюционная диаграмма для случая ГУ2 изображена на рис. 6.21. Из сравнения рис. 6.21 с рис. 6.7 можно видеть, что речь идет о движении вблизи ста-

Напомним, что слово стационарное (в составе термина квазистационарное ) ие означает иезависяшее от времени , а означает установившееся (возможно, достаточно сложное) поведение. Квазистациоиариое поведение близко к установившемуся в некотором смысле (ие определенном в книге). - Прим. ред.

ционарных решенийпо устойчивым ветвям; скачки наблюдаются после перехода параметра L через критические значения, отвечающие точкам поворота на рис. 6.7. Если выбрать коэффициент а, определяющий рост L, слишком большим (например, положив /,(/)= 6--0,002/), то связь между полученной эволюционной диаграммой и диаграммой стационарных решений на рис. 6.7 при малых L уже не будет такой очевидной. Поэтому на выбор этого коэффициента требуется обратить особое внимание. Если мы, наоборот, выберем его слишком малым, то необходимое время вычислений окажется слишком большим.

Jr(0) 8

z 10

120 Ut) UO

Рис. 6.21. Эволюционная диаграмма для задачи 13 при ГУ2, ц = 0,0035, v = = 0,0045, Ро = 6- Ю-*, с = 0,05, с' = 0,025, Dx = 0,01, Dy = 0,45, р = р' = = 3,2. Величина L изменялась по закону L (/)= 6-f 0,0002/; схема (6.4.3), W = 1/2, л = 48, т = 125. В верхней части рисунка приведены характерные профили концентрации х.

На рис. 6.22 представлена эволюционная диаграмма по параметру L для задачи 13 в случае ГУ1 (остальные параметры выбираются такими же, как на рис. 6.21); соответствующая диаграмма стационарных решений не строилась. На этом рисунке, так же как и на предыдущем, приведены характерные профили переменной х для избранных значений длины L. Как и в случае ГУ2, здесь также при увеличении L структура решения становится все более сложной (число максимумов и минимумов на пространственных профилях растет). Более подробно эти результаты обсуждаются в работе [6.32].

) Имеются в виду стационарные (периодические и т. д.) решения уравнений прн постоянных, не зависящих от времени, значениях параметров. - Лрим. ред.

На рис. 6.23 изображена эволюционная диаграмма для задачи И с ГУ2 при таких значениях параметров, когда существуют устойчивые периодические рещения (Л = 2, В = 5,45,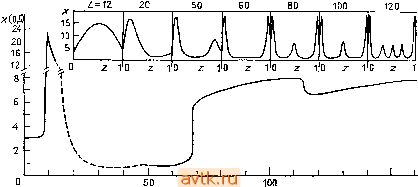

Lif)

Рис. 6.22. Эволюционная диаграмма для задачи 13 при ГУ1. Параметры выбирались такими же, как иа рис. 6.21; схема (6.4.3), w = 1/2, га = 80, т = = 125; сплошные линии - симметричные профили, штриховые - асимметричные профили.

2,6-

О 2 4 6 й L

Рис. 6.23. Эволюционная диаграмма для задачи 11 при ГУ2, Л = 2, В = 5,45, Dx = 0,008, Dy = 0,004, L (t) = 0,45 + 0,0055/; Да; (0) = max [a; (0, /)] - - тш[дг(0,/)], где максимальное и минимальное значения оцениваются для /, меняющегося в пределах одного периода.

Z)x = 0,008, Dy = 0,004). При малых значениях L здесь существует устойчивое пространственно однородное периодическое рещение, которое теряет устойчивость вблизи значения L = 2. При больших значениях L сосуществует большое число устойчивых периодических решений; так, например, при L - 4,5 их

уже минимум пятнадцать (для периодических решений и ГУ2 также действует принцип суммирования решений, см. п. 4.3.1). Все эти решения имеют примерно тот же период, что и однородное решение, т. е. Г л; 3,8. Эволюционная диаграмма, приведенная на рис. 6.23, была построена следующим способом. При L = 0,45 однородное периодическое решение является устойчивым. При изменении L(t) в интервале (0,45; 2,2) в вычисления вводились случайные флуктуации (возмущения) значений решения с амплитудой 0,01, в результате решение перешло из окрестности ветви однородных периодических решений на ветвь неоднородных решений. При этом последовательно (с ростом L{t)) возникают периодические решения со все более и более сложной структурой (имеющие больше максимумов и минимумов). На оси ординат эволюционной диаграммы на рис. 6.23 откладывается величина Ax(0), которую можно рассматривать как амплитуду колебаний на границе системы. Каждый минимум представленной на рисунке кривой отвечал возникновению более сложной структуры. Более подробный лнализ периодических решений задачи 11 представлен в работе [6.33].

Подчеркнем, что построение эволюционных диаграмм для распределенных систем требует большого объема вычислений, особенно в случаях, когда в задаче возникают периодические решения. Особую роль при этом играет подходящий выбор коэффициента а в формуле L = Lo -\- at. К тому же сами эксперименты с указанной величиной (с тем, чтобы определить, какое наибольшее значение а мы можем выбрать) требуют довольно больших затрат машинного времени,

6.7. ЗАДАЧИ

6.7.1. Методом стрельбы решить краевую задачу, возникающую при анализе задачи 16, а именно, редуцированную задачу, описываемую соотношениями (6.1.21), (6.1.16а, с). Выбрать начальное условие в виде

г/(0) = Л1

и воспользоваться методом Ньютона (элементы матрицы Якоби следует вычислять с помощью уравнений в вариациях). Решить эту задачу при следующих значениях параметров: 7 = 20, а = О, р = 0,1, Ф = 1, Shc . Значения начальных приближений для щ выбирать в интервале (0,1; 1). Окончательные значения t]i = 0,37453 и г/(1) = 1,23081. Попробуйте

*> Точнее, решения, близкие к периодическим. - Прим. ред. 23*

решить данную задачу как задачу Коши на отрезке от г = 1 до-/- = 0, полагая у'(1) = г\и и покажите, что задача чрезвычайно чувствительна к точности выбора f\i.

6.7.2. Составить программу метода отображения параметра для задачи 13 с ГУ1 при следующих значениях параметров: = 0,0035; v = 0,0045; ро = 0,0006; 0 = 0,05; с'= 0,025; р = = р' = 3,2, Dx-0, Dy=l. Построить зависимость y{0) - t\ от L. (Для контроля: при t\ == 400 величина L должна приблизительно равняться 30.) Использовать тот же самый метод для случая ГУ2 и (Для контроля: при г/(0) = 200 величина L должна приблизительно равняться 38,1.)

6.7.3. С помощью метода отображения параметра построить зависимость решения уравнения Треша

g- = nsh(ny) (6.7.1)

с граничными условиями

г/(0) = 0, у{1)=1 от параметра п. Указание: использовать подстановку

Y = ny, 1 = пх (6.7.2)

и выбрать начальное условие в виде dY{0)/d= т)[6.8].

6.7.4. Построить бифуркационную диаграмму первичных бифуркаций для задачи И в плоскости параметров р - L ; р = = Dx/Dy при А = 2, Dx = 0,0016, В = 4,6.

6.7.5. Построить бифуркационную диаграмму первичных бифуркаций для задачи 13 в плоскости параметров р - L; р'= = р, л = 0,0035, v = 0,0045, ро = 6.10-\ с = 0,05, с'= 0,025, Dx = 0,Ol, Dy = 0,45. Показать, что существуют только вещественные бифуркационные длины.

6.7.6. С помощью методики, описанной в п. 6.3.2.2, рассчитать точку поворота на диаграмме стационарных решений задачи 11, изображенной на рис. 6.3 или 6.4. При вычислении производных в третьей строке матрицы Якоби для метода Ньютона можно воспользоваться соответствующими разностными формулами. Выбор начального приближения произвести на основе указанных рисунков.

6.7.7. Составить программу для динамического моделирования (т. е. для численного решения задачи Коши. - Ред.) уравнений (6.4.30)-аппроксимации для задачи 16. Рассчитать и построить соответствующие фазовые портреты для значений Lw = 1; 2,5; 3; 4; 5 при следующих значениях остальных параметров: у = 20, р = 0,2, ф=1,5, NucxD, ShcxD, а = 2. Показать, что существует такое значение Lw*, что при Lw >

> Lw* единственное стационарное решение теряет устойчивость и возникает устойчивое периодическое решение.

При значениях параметров у = 20, р = 0,4, а = 2 данная задача имеет три стационарных решения для интервала значений Ф (~0,65). Построить фазовые портреты для указанного случая при Lw= 1; 1,5; 2; 2,5; 3; 3,5; 5. Покажите, что существует значение Lw*, при котором одно из стационарных решений теряет устойчивость. Затем постройте фазовый портрет для значения Lw, которое на 0,1 превышает Lw*. При этом вокруг указанного стационарного решения возникает периодическое решение. Для динамического моделирования используйте какой-либо из методов, описанных в § 5.7, лучше всего с автоматическим изменением шага интегрирования.

ЛИТЕРАТУРА

[6.1] Villadsen J., Michelsen М. L.: Solution of Differential Equation Models by Polynomial Approximation, Prentice-Hall, Englewood Cliffs, N. Y., 1978.

[6.2] Finlayson B. A.: The Method of Weighted Residuals and Variational Principles. Academic Press, New York, 1972.

[6.3] Gottlieb D., Orszag S. A.: Numerical Analysis of Spectral Methods: Theory and Applications. NSF-CBMS Monograph 26, SIAM, Philadelphia, 1978.

[6.4] Hlavacek V., Kubicek M., Caha J.: Chem. Engng. Sci. 26 (1971), 1737, 1743.

[6.5] Fox L.: The Numerical Solution of Two - Point Boundary Problems

in ODE. Oxford University Press, London, 1957. [6.6] Keller H. В.: Numerical Methods for Two-Point Boundary Value

Problems. Blaisdell, Waltham, MA, 1968. [6.7] Roberts S. M., Shipman J. S.: Two-Point Boundary Value Problems:

Shooting Methods. American Elsevier, New York, 1972. [6.8] Kubicek M., Hlavacek V.: Numerical Solution of Non-linear Boundary

Value Problems with Applications. Prentice-Hall, Englewood Cliffs,

N. Y., 1983.

[6.9] Na T. Y.: Computational methods in engineering boundary value problems. Academic Press, New York, 1979. [Имеется перевод: На Ц. Вычислительные методы решения прикладных граничных задач.-М.: Мир, 1982. - 294 с] [6.10] Kubicek М.: Numericke algoritmy re§eni chemicko - inzenyrskych uloh. SNTL, Praha, 1983.

[6.11] Holodniok M., Kubicek M., Hlavacek V.: J. Fluid Mech. 108 (1981), 227.

[6.12] Kubicek M., Holodniok M., Hlavacek V.: Computers and Fluids 4 (1976), 59.

6.13 6.14 6.15 6.16 6.17

Kubicek M., Hlavacek V.: Chem. Engng. Sci 27 (1972), 743, 2095. Kubicek M., Hlavacek V.: J. Inst. Math. Appl. 12 (1973), 287. Kubicek M.. Ryzler V., Marek M.: Bioph. Chem 8 (1978), 235. Holodniok M., Kubicek M.: Sbornik VSCHT К 17 (1982), 109. Kubicek M., Marek M., Hustak P., Ryzler V.: Bifurcation, Multiplicity and Stability in Reaction - Diffusion Systems. Proceedings of the Stir Symposium Computers in Chemical Engineering, Vysoke Tatry, October 5-9, 1977, 903.

[6.18] Kubicek М., Hofmann Н., Hlavacek V.: Chem. Engng. Sci. 34 (1979) 593

6.19 Hlavacek V., Kubicek M., Marek M.: J. Catalysis 15 (1969), 17, 31. 6.20] Jensen K. F., Ray W. H.: Chem. Engng. Sci. 37 (1982), 199.

6.21 Kubicek M., Holodniok M.: Chem. Engng. Sci. 39 (1984), 593.

6.22 Roose D., Hlavacek V.: SlAM J. Appl. Math., 45 (1985), 879.

6.23 Forsythe G. E., Wasow W. R.: Finite-Difference Methods for Partial Differential Equations, Wiley, New York, London, 1960. [Имеется перевод: Вазов В., Форсайт Дж. Разностные методы решения дифференциальных уравнений в частных производных. - М.: ИЛ, 1963.- 487 с]

[6.24] Mitchell А. R.: Computational Methods in Partial Differential Equations. Wiley, London, 1969.

[6.25] Fox L., ed.: Numerical Solution of Ordinary and Partial Differential Equations. Pergamon Press, New York, 1962.

[6.26] Richtmyer R. D.: Difference Methods for Initial - Value Problems. In-terscience, New York, 1957. [Имеется перевод: Рихтмайер P. Д. Разностные методы решения краевых задач.- М.: ИЛ, 1960.- 262 с]

[6.27] Mitchell А. R., Wailt R.: The finite element method in partial differential equations. Wiley, New York, 1978. [Имеется перевод: Митчелл Э., Уэйт Р. Метод конечных элементов для уравнений с частными производными.-М.: Мир, 1981. -216 с]

[6.28] Бабушка И., Витасек Э., Прагер М. (Babuska 1., Vitasek Е., Pra-ger М.). Численные процессы решения дифференциальных уравнений. - М., Мир , 1969.

6.29] Eigenberger G., Butt J. V.: Chem. Engng. Sci. 31 (1976), 681.

6.30] Villadsen J. V., Stewart W. E.: Chem. Engng. Sci. 22 (1967), 1483.

6.31] Sevcikova H., Kubicek M., Marek M.: Mathematical Modelling in Science and Technology, Ed. X. J. R. Avula, R. E. Kalman, A. I. Liapis, E. Y. Rodin. Pergamon Press, New York, 1984, p. 477.

6.32 Marek M., Kubicek M.: Bull, of Math. Biology 43 (1981), 259.

;6.33] Raschman P., Kubicek M., Marek M.: Sbornik VSCHT К 17 (1982), 151.

6.34] Stoer J., Bulirsch R.: Introduction to Numerical Analysis. Springer, New York, 1980.

[6.35] Flaherty J. E., Paslow P. S., Shephard M. S., Vasilakis J. D., Eds.: Adaptive Methods for Partial Differential Equations. SlAM, Philadelphia, 1989.

ДОПОЛНИТЕЛЬНАЯ ЛИТЕРАТУРА

Kernevez J. P.: Enzyme Mathematics. North-Holland Publ. Сотр., Amsterdam, 1980.

Othmer H. G., Scriven L. E.: I & E. C. Fundam. 8 (1969), 303.

Murray J. D.: Lectures on Nonlinear Differential Equation Models in Biology. Clarendon Press, Oxford, 1977. [Имеется перевод: Марри Дж. Нелинейные дифференциальные уравнения в биологии. - М.: Мир, 1983.- 397 с]

Fife Р. С: Mathematical Aspects of Reacting and Diffusing System. Springer, Berlin, 1979.

ПРИМЕЧАНИЯ РЕДАКТОРА ПЕРЕВОДА

Практически фазовый портрет обычно считают известным, если:

а) найдены все особые траектории (положения равновесия, циклы, сепаратрисы седел и т. п.),

б) вычислено (изображено) несколько типичных неособых траекторий, так что ясно видно их асимптотическое поведение.

Несколько замечаний о бифуркациях в уравнениях с симметрнями.

1) Предположим, что система x = f(x, а) допускает симметрию g и некое положение равновесия х* (а) симметрично (инвариантно относительно отображения g). Тогда вовсе не обязательно, чтобы прн изменении параметра а происходила бифуркация с потерей симметрии, т. е. чтобы возникали несимметричные равновесия наряду с симметричным (илн вместо него). Пусть, например, g - отражение в плоскости Х\=0. Тогда возможны:

а) бифуркации, при которых симметрия внешне никак ие сказывается - все события разворачиваются в (инвариантной) плоскости Xi = 0;

б) бифуркации с потерей симметрии (типа вилка ). Оба варианта одинаково вероятны - отвечают обращению в нуль одной функции'.

2) Если симметрия, которой обладают уравнения, достаточно богата, то возможна постепенная потеря симметрии прн бифуркациях. Простейший пример. Пусть система x = f(x, а) инвариантна относительно отражений в каждой нз координатных плоскостей х, = 0: каждая функция fk(x) нечетна по переменной х^ и четна по остальным х,. Симметричное положение равновесия х = О (не зависящее от а) может прн изменении а породить> пару положений равновесия, у которых, скажем, х^ = ±Ci (а) (¥=0), остальные X, равны нулю. Прн дальнейшем изменении параметра от этих точек могут ответвиться новые положения равновесия, имеющие больше не равных нулю координат (инвариантных относительно меньшей группы симметрии).

Матрица линеаризации А в точке х*(а) (прн подходящем базисе) имеет здесь вид

где С есть (л-1)-мерная матрица. Случай а) отвечает условию det С = 0,. случай б)-условию В = 0.

3) Если система инвариантна относительно непрерывной группы преобразований g, то при бифуркации с потерей симметрии может возникнуть континуум положений равновесия (переводимых друг в друга преобразованиями группы). Простейший пример доставляет система 3 уравнений, инвариантных относительно всех поворотов вокруг некоторой оси /. Здесь возможны как бифуркации с сохранением симметрии (положения равновесия остаются на оси /), так и возникновение целого семейства (окружности) положений равновесия.

4) Бифуркация типа вилка возможна, конечно, и в системах, не обладающих какой-либо симметрией. Однако при малом возмущении такой системы вилка исчезает и в этом смысле является нетипичной (см. [2.9], § 31).

3 Авторы не рассматривают здесь случаев, когда прн изменении параметра а период Т{а) обращается в бесконечность. Два сценария возможны уже в двумерных системах (и часто наблюдаются). Это: (а) превращение цикла в петлю сепаратрисы; (б) рождение на цикле пары положений равновесия (оба эти случая упомянуты в конце § 2.4). В случае (а) Г(а)~ ~1п|а -а*-; в случае (б) Г(а)~а - a{-K Здесь а* - критическое значение параметра.

О бифуркациях периодических решений в системах с симметриями. Сделанные выше замечания о бифуркациях положений равновесия остаются в силе (с небольшими изменениями).

Напомним, что симметричное периодическое решение х = р(/) g-инвариантного уравнения-это такое решение, траектория которого у инвариантна относительно отображения g (g(y)= у).

Если g{y) = у, то есть две возможности.

(а) gP(0= Р(0 при всех /.

(б) gp{t)= p{t + 8); типичный случай а - Т/2, где Г (наименьший) период р(/). Для случая (а) справедливо все то, что сказано выше про бифуркации симметричных положений равновесия. Случай (б) требует отдельного рассмотрения.

Обычно критерием устойчивости называют набор условий, близких к необходимым и достаточным. Чтобы получить критерий, здесь нужно до-бавить:

Если хотя бы один мультипликатор лежит вне единичного круга (р*> 1), то решение p{t) не является орбитально устойчивым .

Приведенная здесь наглядная интерпретация одномерных показателен Ляпунова полезна, но не точна: показатели Ляпунова определяют поведение решений линеаризованной (а не исходной) системы. В частности, если Я(хо, е)<0, то траектория у(хо-Ь ее) (для некоторого малого, но фиксированного е!) не обязана прн /->-foo приближаться к у(Хо)-

Короткая гл. 3 и значительная часть § 5.4 посвящены явлению, обычно не происходящему в однопараметрических системах дифференциальных уравнений, а именно пересечению ветвей на диаграмме стационарных решений. Некоторым основанием для отдельного рассмотрения этого вопроса является то, что задачи о распределенных системах часто имеют семейства тривиальных решений, существующих при всех значениях параметра. Бифуркация типа вилка в таких системах вполне обычна.

Тем не менее равноправное изучение точек поворота и точек ветвления не кажется вполне правильным: бифуркация слияния ( = бифуркация седло - узел ) встречается практически в любой задаче, а для пересечения однопараметрических семейств стационарных решений нужны специальные лричины.