ведено периодическое решение задачи 11 для случая ГУ1. На рисунке показано несколько типичных профилей переменной х для нескольких моментов времени в течение одного периода.

В п. 6.3.3.2 мы определили точку комплексной бифуркации для задачи 14 (см. табл. 6.11). Динамическое моделирование уравнений (Р14-7), (Р14-8) для значений параметра Da из окрестности Da+ж 0,1254(Da < Da+) показало, что в данном случае существует ветвь периодических решений для значений Da е (0,122; 0,1254). Значения конверсии и температур на входе в реактор и на выходе из него, т. е. величины y{0,t), S(0,t) и y{l,t), 6(1,), представлены на фазовой диаграмме у - в (рис. 6.14).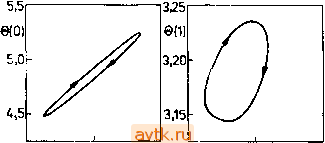

0.70

0,75 М 0,30 0,98

0,99 у(1) 1,0

Рис. 6.14. Устойчивое периодическое решение задачи 14 (две проекции); Y - оо, В = 12, Р = 2, вс = О, Da = 0,123, Le = 1.

Продолжение периодических решений по параметру для указанного случая можно проводить, применяя вышеописанный подход (т. е. численно моделируя процесс стабилизации) для некоторой последовательности значений данного параметра. Другая возможность состоит в использовании квазистационарного описания (см. § 6.6).

Процесс стабилизации (установления) обладает тем очевидным недостатком, что с его помощью можно получать только устойчивые периодические решения. Рассмотрим теперь два других подхода, которые позволяют находить и неустойчивые периодические решения.

6.5.1.1. Метод стрельбы в рамках метода прямых

Если для аппроксимации параболических уравнений (4.3.7) воспользоваться методом прямых (п. 6.4.5), то условия (6.5.1) принимают вид ( = 0)

XtiT) = Xi{0), yi{T) = yi(Q), t=l, 2, n-l. (6.5.2)

> Смешанное условие включает значения решения на обоих концах отрезка О < < 7 . - Прим. ред.

Тем самым мы получаем нелинейную краевую задачу (см., например, (6.4.24)) для 2{п-1) дифференциальных уравнений первого порядка со смешанными граничными условиями (6.5.2). Ситуация здесь полностью аналогична той, которая имела место для задач, прямо приводящих к обыкновенным дифференциальным уравнениям (ср. (5.8.1), (5.8.2)), однако размерность изучаемой системы оказывается большой. Таким образом, мы можем использовать методику § 5.8, которая основывалась на методе стрельбы, а также на идее алгоритма продолжения DERPER (см. п. 5.8.4).

Продемонстрируем использование метода прямых на примере задачи 11 с граничными условиями первого рода. Используя трехточечную замену по переменной z, получим

dx. D

- = j;-{Xi-i - 2xi + Xi+i) + f{Xi, yi), (6.5.3а>

= -{yi-\ - 2yi + yi+\) + g{Xi, уд (6.5.3b)

при /=1,2.....n - 1; h = \/n, xo = Xn = x, у^ = уп = у.

Для численного решения были выбраны следуюшие параметры задачи: А = 2, 5 = 5,45, = 0,008, Dy = 0,004. В случае ГУ1 мы имеем тривиальное стационарное решение x(t) = х = Л, y{t)y = B/A, устойчивое при L->-0. С помощью методики, описанной в 6.3.1, находим критическую длину, отвечающую комплексной бифуркации Li* = 0,5130 (вещественные бифуркации при изменении параметра L не наблюдаются). Следовательно, тривиальное решение является устойчивым при

Le(0, Li) и неустойчивым при L>Lt- При значении L - Lt от ветви тривиальных решений отходит ветвь устойчивых периодических решений. Диаграмма периодических решений, построенная для вышеприведенной системы с помощью алгоритма продолжения DERPER, показана на рис. 6.15.

Добавим еще несколько замечаний по поводу этого рисунка.

Как уже сказано, при значении параметраL = от ветви стационарных решений отходит ветвь периодических решений (существующая при L > L\). Этой ветви принадлежит, в частности, устойчивое периодическое решение при L = 0,75, показанное на рис. 6.13. Периодические решения с указанной ветви, как это следует из рис. 6.13, являются пространственно симметричными: для всякого t и 2е[0, 1] имеют место соотношения

x{z, t) = х{1 - z,t); y{z,t) = y{l - z,t). В точке, обозначенной на рис. 6.15 буквамиТПС, периодические решения утрачивают устойчивость (происходит бифуркация типа +1 ) и от исходной ветви симметричных решений отделяется ветвь устойчивых пространственно несимметричных решений. Заметим, что в данном случае имеются две такие ветви; они содержат периодические решения, которые (при заданном L) обладают одинаковым

т

Рис. 6.15. Диаграмма периодических решений для задачи 11 при ГУ1; зависимость периода Т (А = 2, В = 5,45, Dx = 0,008, Dy = 0,004). Метод прямых (6.5.3), л = 20. Сплошные линии - устойчивые периодические решения, штриховые - неустойчивые периодические решения, Гь Гг, Тз - точки бифуркации типа тора, ТПС - точка бифуркации с потерей симметрии.

периодом Т. При этом для любого t их пространственные профили являются взаимно симметричными, т. е. при произвольном 2е[0, 1] выполняется xi(z, t) = х^ЦХ-z, t), у^Цг,() = = t/(2)(l-z,t), где верхний индекс определяет ветвь решений.

В табл. 6.13 приведены 14 наибольших по абсолютной величине мультипликаторов, а также величины периода Т, для неустойчивого периодического решения в случае L= 1,5 (обозначенного на рис. 6.15 кружком) при двух различных значениях л = 20 и /г = 40. Напомним, что при /г = 20 матрица монодромии имеет 38 собственных чисел, а при /г = 40 у нее 78 собственных чисел. Остальные собственные числа, которые не приведены в таблице, оказываются близкими к нулю. Из таблицы

Таблица 6.13. Собственные числа матрицы монодромии и период Т в зависимости от разбиения отрезка 02 1. Периодическое решение при L-l,5 (иа рис. 6.15 оно обозначено кружком).

ВИДНО, что главные мультипликаторы (по абсолютной величине большие 1/2) для обоих разбиений оказываются практически одними и теми же. Поскольку Я,2,з|> 1, данное периодическое решение оказывается неустойчивым. Величина Я,2,з| невелика, и можно говорить о слабой неустойчивости: при динамическом моделировании с начальным условием вблизи этого решения соответствующая траектория будет очень медленно разматываться , уходя от этого периодического решения.

На каждой из ветвей пространственно несимметричных решений была найдена точка бифуркации, при которой рождается инвариантный тор (обозначенная как Г] на рис. 6.15; обе ветви на изображенной здесь диаграмме решений сливаются).

Таблица 6.14. Сравнение бифуркационных значений L* точки Tl (рис. 6.15) при различных п.

В табл. 6.14 приведены бифуркационные значения L* для точки Tl, найденные при различных п. Значение L*, подсчитанное с помощью экстраполяции по Ричардсону для п = 20 и

2,7 2,9 3,1 x{Q,5)

Рис. 6.16а. Проекция орбиты отображения Пуанкаре при L = 1,4050.

п = 40, иллюстрирует точность определения этой величины в зависимости от п.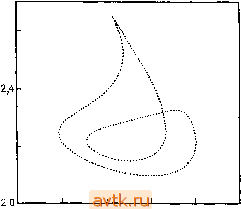

2,7 2,9 3,1 (0,5)

Рис. 6.16Ь. Проекция орбиты отображения Пуанкаре при L - 1,4070.

На рис. 6.15 показаны, кроме того, еще две другие точки бифуркации рождения инвариантного тора (Гг, Гз), лежащие на другой ветви периодических решений.

В окрестности точки бифуркации Г] при L> L* мы с помощью динамического моделирования нашли устойчивый инвариантный тор. На рис. 6.16а изображена проекция орбиты отображения Пуанкаре для траектории на этом инвариантном торе. При возрастании величины L указанный тор теряет устойчивость и рождается удвоенный устойчивый тор (рис. 6.16Ь). При этом отображение Пуанкаре в обоих случаях определяется уравнением x(0,3;?) = 2. При возрастании значений параметра L можно наблюдать последовательность нескольких дальнейших удвоений тора. Учитывая слабую неустойчивость существующих одновременно периодических решений, можно было наблюдать медленное приближение траектории к устойчивому инвариантному тору. Если начальная точка выбиралась в окрестности периодического решения, то для того чтобы решение стабилизировалось на устойчивом инвариантном торе, нам приходилось интегрировать в течение времени порядка нескольких тысяч периодов.

6.5.1.2. Метод конечных разностей

Заменим дифференциальные уравнения (4.3.7) конечно-разностными по схеме Кранка-Николсона (6.4.3) при да = 0,5 и т = Т/т. Мы получим систему

f (4+ - 4) - W - 24+цгп -

-f{Xi ,У1 ) = 0, (6.5.4а)

1 + 1/2 = I (/ + 1 + y + U2 =1 + 1 + yV)

-(4+. уГ ) = 0 (6.5.4Ь)

при /= 1,2, п-1 и / = 0,1.....т-\. Граничные условия 1-го рода, дают уравнения (6.4.4) для / = -1, О, 1, ... т - \, а из условия периодичности (6.5.1) находим

xa-xf = Q, y°.-yf = 0, 1=1, 2, n-1. (6.5.4с)

Тем самым в целом у нас имеется = 2(п-f 1) (т-f 1) уравнений (6.5.4а), (6.5.4Ь), (6.5.4с), (6.4.4) относительно -(-1 неизвестных xi, у[, Т. Точно так же, как и в п. 5.8.2, зафиксируем какую-либо одну компоненту решения, например х°, оста-

ВИВ период Т в качестве неизвестной. Полученную систему нелинейных уравнений можно решать, например, с помощью метода Ньютона, причем системы линейных алгебраических уравнений, возникающие на каждой итерации, решаются с помощью подходящего алгоритма для почти ленточных матриц. Получающиеся при этом системы имеют большие размеры, и поэтому этот метод удобно реализовывать лишь на достаточно мощных ЭВМ и при не слишком больших размерах тип. Периодическое решение задачи 11, найденное таким методом для относительно редкой сетки узловых точек, представлено в табл. 6.15.

Таблица 6.15. Периодическое решение задачи 11 с граничными условиями типа ГУ1, найденное из коиечио-разностиых уравнений (6.5.4); А = 2, В = 5,45, Dx = 0,008, Dy = 0,004, L = 0,75, m = 19, л = 5. Окончательное значение Г = 3,3073; в качестве фиксированного значения одной из неизвестных выбиралось у\ - 3,4. Найденное решение является симметричным по переменной z относительно точки z ~ 0,5; поэтому х^ = х1 х^ = х{, - У2

На рис. 6.17 показан еще один способ изображения периодического решения в распределенных системах (ср. с рис. 6.13). Этот способ удобен в тех случаях, когда профили решения качественно сохраняют свою форму и изменяются не слишком сильно (так, чтобы на рисунке не перекрывать друг друга).

Для продолжения периодического решения при изменении параметра, например параметра L, можно разработать алгоритм, основанный на конечно-разностной схеме (6.5.4). Вблизи точек поворота величину L необходимо рассматривать как неизвестную и последовательно изменять значения какой-либо другой переменной, например Т.

6.5.2. Решения волнового характера

Рассмотрим сначала уравнения с частными производными (4.3.7) без граничных условий на бесконечном интервале изменения независимой переменной z. Подстановка

X (г, /) = Ф (2 - ct), у (2, t) = {z- ct) (6.5.5)

в уравнения (4.3.7) приводит к системе двух обыкновенных диф-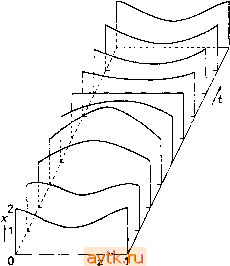

Рис. 6.17. Периодическое решение задачи 11 при ГУ1, найденное с помощью разностных уравнений (6.5.4): m = 18, п - Ъ, А - 2, В - 5,45, Дх = 0,008,

Dy = 0,004, Т = 3,3073.

ференциальных уравнений 2-го порядка для функций ф() и t(l):

-сф = ф -Ь/(ф, ф), ( =

(6.5.6)

-c = -jr + g{P, Ф).

Периодические решения, а также гомоклинические и гетероклинические траектории системы (6.5.6) соответствуют решениям волнового типа исходной системы.

Обратимся теперь к случаю конечного промежутка изменения переменной z и рассмотрим вновь систему (4.3.7) с соответствующими граничными условиями.

Заметим, что нелинейные дифференциальные уравнения с частными производными параболического типа могут обнаруживать характерные свойства гиперболических систем: они могут иметь решения, которые можно назвать решениями волнового характера на конечном интервале изменения пространственной переменной. Изложение мы будем вести на примере задачи 12.

В первой части этого пункта мы рассмотрим решения типа импульса, а во второй части исследуем волну типа фронта (см. § 2.6).

6.5.2.1. Волна типа импульса

Волновые решения уравнений (4.3.7) зависят от свойств системы, получающейся при £)х->0, Z)y->0. Рассмотрим за-дачу 12, т. е. зададим / и формулами (Р12-1) и (Р12-2). Выберем следующие значения параметров: у = 3, Vo==0,01, р =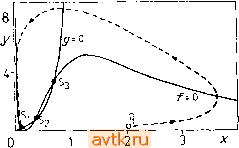

Рис. 6.18. Фазовый портрет системы (Р4-1), (Р4-2): у = 3, vo = 0,01, р = = 1,5, 6=1, а = 12; Si, Sj, S3 - стационарные решения.

= 1,5, 6=1, а =12. Соответствующая система при Dx = - Dy=Q (см. (Р4-1), (Р4-2)) будет иметь три стационарных решения:

S,: a;i = 0,11566, у, = 0,19618 (устойчивый фокус);

S2: д:2 = 0,37278, /2 = 0,89151 (седло);

S3: д;з = 0,70063, г/з = 3,51059 (неустойчивый узел).

На рис. 6.18 кроме стационарных состояний показаны нулевые изоклины функций f и g. Пунктиром изображена одна из траекторий. Из рисунка видно, что относительно малое возмущение стационарного состояния Sj может вызвать изменение переменных состояния по циклу возбуждения ; система уходит при этом далеко от устойчивого стационарного состояния.

(Если выбрать начальное условие справа от Si за нулевой изоклиной функции f, то фазовая траектория закручивается вокруг состояния S3, и лишь потом устремляется к Si.)

Выберем теперь для уравнений (4.3.7) в задаче 12 следуюшие граничные условия:

z = Q: X (О, t) = Хр, у (О, t) == г/ (6.5.7а)

2=1:

дх (1. t) dz

= 0,

ду (1, Г)

= 0.

(6.5.7Ь)

Если Хр = Xi [xi и г/1 представляют собой значения хну в стационарном состоянии Si, см. выше), то задача имеет тривиальное решение x(z,t) = Xi, y{z,t)y\, которое является устойчивым. Таким образом, величина Хр характеризует собой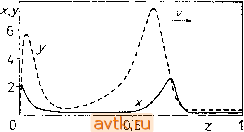

Рис. 6.19. Бегущая волна в задаче 12 при ГУ2: у = 3, vo = 0,01, б = 1, а = 12, Дх = 0,008, Ду = 0,004, L = 2,5, Хр = 2; v = 0,108,

= 1,5, = 8,0.

возмушение переменной х на левом конце промежутка. На правом конце заданы граничные условия второго рода, которые описывают непроницаемую для исследуемых веществ стенку. Уравнения (4.3.7) решались посредством конечно-разностной схемы типа Кранка - Николсона с заменой нелинейности с помощью отрезка ряда Тейлора (см. § 6.4) при п= 160, т = 0,1. Если выбирать Хр не слишком близко к Хи то в системе начинают возникать волны концентрации, бегущие от 2 = 0 до 2=1. Одна из таких волн изображена на рис. 6.19 (для некоторого момента времени t). Эта волна возникла вблизи левого конца промежутка, в точке 2 = 0,2 ее форма оказалась уже достаточно развитой, далее она сохраняет свой вид до значения ) 2 = 0,8, после чего на правом конце промежутка она исчезает в силу действия граничных условий (6.5.7Ь). Определим скорость движения волны как v - dzv/dt, где Zv есть, например, координата вершины волны. Далее, определим период

Имеются в виду координаты вершины волны. - Прим. ред.