ОТ у = у, где W(у) = у', z(y)=z ло у = \. После этого полагаем 2(1) = ф (ср. аналогичный процесс вычисления отображения Пуанкаре, п. 5.9.2). Полученные таким образом значения ф для последовательности значений г\ приведены в табл. 6.9. Из этих данных видно, что при Р = 0,4 для определенного интервала значений ф (например для Ф = 0,3) существует три решения исходной краевой задачи. Читатель может сравнить результаты, полученные при р = 0,05, с результатами, приведенными в табл. 6.1.

Таблица 6.9. Результаты применения метода отображения параметра для задачи 16 (у = 20, а = 0). Значения Ф.

= 0,05

Р = 0,2

3 = 0,25

Р = 0,4

0,95

0,85

0,75

0,65

0,55

0,45

0,25

0,02

0,01

0,001

0,31639 0,55044 0,63823 0,71757 0,86298 1,00294 1,07453 1,14920 1,41268 1,52519 1,66101 2 08042 3,06664 3,49531 4,92385

0,29742 0,45896 0,50212 0,53330 0,57434 0,60044 0,61114 0,62160 0,66137 0,68178 0,70946 0,81140 1,09463 1,22341 1,65658

0,29139 0,43259 0,46467 0,48487 0,50498 0,51174 0,51324 0,51468 0,52646 0,53618 0,55150 0,61687 0,81559 0,90755 1,21770

0,27419 0,36368 0,37080 0,36820 0,34981 0,32628 0,31494 0,30455 0,28254 0,27952 0,27975 0,29753 0,37686 0,41554 0,54695

Другим примером, на котором мы рассмотрим возможности метода отображения параметра, является система типа реакция-диффузия (4.3.16) при Dy-vO. В этом предельном случае второе уравнение системы (4.3.16) сводится к конечному уравнению вида

g{x,y) = 0, (6.2.51)

решая которое, мы находим зависимость у{х) (часто в аналитическом виде). Подстановка в уравнение (6.1.1) дает

= -!{х, y{x)) = ~-f(x).

Положив

l = Lz,

(6.2.52)

(6.2.53)

получим уравнение, не содержащее параметра L:

-0-=-fW. (6.2.54)

Рассмотрим для примера граничные условия 1 рода (4.3.9). Для уравнения (6.2.54) они принимают вид

1 = 0: х = х; l = L: х = х. (6.2.55)

Зададим дополнительно при = 0

= Л. (6.2.56)

после чего проинтегрируем уравнение (6.2.54) от = 0, где л-(0) = х, х'(0) = п. ДО такого значения = L, где x{L) - x. Это значение L мы и сопоставим выбранному х\.

€.3. НАХОЖДЕНИЕ ТОЧЕК ВЕТВЛЕНИЯ

В этом параграфе мы рассмотрим итерационные методы для нахождения точек ветвления стационарных решений распределенных систем. В п. 6.3.1 мы будем находить так называемые точки первичной бифуркации. Пункт 6.3.2 посвящен более сложным (вторичным) бифуркациям.

в.3.1. Первичные бифуркации

Некоторые задачи обладают так называемыми тривиальными решениями, не зависящими от части параметров. К ним, в частности, относятся системы типа реакция - диффузия , описанные в гл. 4. Тривиальное стационарное решение для такой двухкомпонентной системы (4.3.5), (4.3.6) однородно по пространству, т. е. имеет вид

х{г)х, y(z)y. (6.3.1)

Оно не зависит от величины параметра L, задающего размеры системы, а также от величины коэффициентов диффузии

и Dy.

Значения х и у определяются уравнениями /(х, г/) -О, £{х, у) = О и могут, естественно, зависеть от параметров, входящих в функции fug. При изменении этих параметров могут происходить бифуркации, не нарушающие пространственной однородности. Их можно исследовать методами, описанными в гл. 5.

В этом пункте мы рассмотрим бифуркации тривиальных решений, нарушающие пространственную однородность и связан-

ные с изменением параметра L - размера системы. Такие бифуркации мы будем называть первичными.

Устойчивость тривиального решения (6.3.1) определяется собственными числами > линеаризованного оператора [2.32]

Ox

Dy d

(6.3.2)

при соответствующих (однородных) граничных условиях (типа ГУ2 или ГУ1). Здесь

df{x,y) ду dg (ж, у)

df (X, у)

11- дх

dg (х, у)

21---

12 = 22

(6.3.3)

Тривиальное решение (х, у) устойчиво, если все собственные числа оператора 2 имеют отрицательную вещественную часть и неустойчиво, если хотя бы одно собственное число имеет положительную вещественную часть.

Обсудим теперь устойчивость тривиального решения в зависимости от величины параметра L и типа граничных условий. Рассмотрим сначала очень малые L. В случае ГУ1 при L-+O (точнее, при L < Lmin) всякое тривиальное решение будет устойчивым [6.17]. В случае же ГУ2 вопрос об устойчивости при решается в зависимости от поведения системы при отсутствии пространственных градиентов. (Более формально - от поведения системы обыкновенных дифференциальных уравнений, получающейся при Dx = Dy = 0). Именно, если все собственные числа матрицы

и, 12 L 21, 22

лежат в левой (комплексной) полуплоскости, тривиальное решение будет устойчивым в случае ГУ2 при L->--)-0. Наоборот, наличие собственного числа матрицы А с положительной вещественной частью влечет за собой неустойчивость тривиального решения в случае ГУ2.

С ростом L какое-нибудь из собственных чисел оператора может пересечь мнимую ось. При этом в результате веществен-

> Точнее, спектром 2; подробности см. в работе [2.32]. (Здесь это уточнение не нужно: спектр оператора 2 совпадает с совокупностью его собственных значений.-Ред.)

21.

которая имеет один и тот же вид для ГУ1 и ГУ2; 2) вектор есть собственный вектор матрицы А„. Собственныечисла Я, матрицы А„ - корни характеристического уравнения

l--Pn{L)l + Qn{L) = Q, (6.3.7)

где

Pn{L) = an + a-{D, + Dy)E(n), (6.3.8)

Q (L) = Z),Z)£f , - {Da + Da ) + a a, - a a . (6.3.9)

Для того, чтобы k = Q было собственным числом оператора т. е. чтобы имела место вещественная бифуркация, необходимо чтобы при некотором

Q (Z.) = 0. (6.3.10)

Для точки первичной комплексной бифуркации должно выполняться условие

Р„() = 0, Q ()>0. (6.3.11)

Поскольку все собственные функции S имеют вид (6.3.4) (или т.Ъ)).-Прим. ред.

НОЙ или комплексной бифуркации (бифуркации Андронова - Хопфа) может появиться новое решение (нелинейной) задачи. Значение параметра L, соответствующее первичной бифуркации, называют первичной бифуркационной длиной. Это значение находится следующим образом.

В рассматриваемом случае (тривиального стационарного решения) оператор S имеет постоянные коэффициенты и его собственные функции выписываются в явном виде. А именно:

в случае ГУ1: и = [с„ sin ( яг), rf sin( nz)], =1, 2,

(6.3.4)

в случае ГУ2: и = [с„ cos ( яг), rf cos( nz)], = 0, 1, 2.....

(6.3.5)

Подставив эти выражения в равенство Sa = Хи, мы получаем: 1) собственное число X оператора соответствующее собственной функции (6.3.4) или (6.3.5) при определенном значении п, одновременно является собственным числом матрицы

Значение £* ), которое удовлетворяет соотношению (6.3.10), не зависит от :

x У

- 4Z),Z)y ( 022 - 12021)] }. (6.3.12)

Мы можем получить два, одно или ни одного значения Е*, для которых имеет место вещественная бифуркация. После этого находим бифуркационную длину

(п) 1. 2

V42

если Е* > 0. Из последней формулы также следует, что

(6.3.13)

(6.3.14)

для обеих групп бифуркационных длин (определяемых индексами 1 и 2 в выражении (6.3.13)). Величину Ljj называют эле-

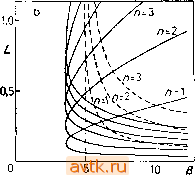Cf.-\ Л2 Лз 0<4 <<

Рис. 6.10. Бифуркационная диаграмма первичных бифуркаций; а) общая схема, Ъ) для задачи 11, Л = 2, Dx = 0,0016, Dy = 0,008; сплошные линии - Q = О, прерывистые - Р = 0.

ментарной бифуркационной длиной; остальные бифуркационные длины оказываются кратными элементарным бифуркационным длинам.

Для значения L+, при котором имеет место комплексная бифуркация, из соотношений (6.3.11) находим

Dx-f Dy

. Он + 022 .

Q. (i(t,) > 0.

(6.3.15)

Формула (6.3.14) остается справедливой и в этом случае, т. е.

L(t) = L(t). (6.3.16)

Условия существования бифуркационных длин в зависимости от величины отнощения Dx/Dy и коэффициентов а приведены, например, в работе [5.10]. Если построить графики зависимостей величин L* и L+ от другого параметра задачи а, то мы получим бифуркационную диаграмму первичных бифуркаций. Такого рода бифуркационная диаграмма представлена схематически на рис. 6.10а. При а < ai не существует какой-либо бифуркационной длины, при а е (ai, 2)11 ( з. oc-t) имеются два значения Ljj а при (аг, аз)[](а4, оо) имеются два значения

Ljj и одно значение Ly На рис. 6.10b эта диаграмма изображена для задачи 11 (показаны также значения некоторых кратных бифуркационных длин L( )). Читатель может сравнить точки первичных бифуркаций на рис. 6.3 и 6.4 со значениями L на рис. 6.10b.

6.3.2. Нахождение точек вещественной бифуркации

Рассмотрим теперь две группы методов нахождения точек вторичных вещественных бифуркаций. (Эти методы, разумеется, пригодны и для нахождения точек первичной бифуркации, однако для этого случая выще описан более простой подход.) Первую группу составляют разностные методы, тогда как методы второй группы основываются на методе стрельбы.

6.3.2.1. Разностные методы

Рассмотрим для простоты краевую задачу (6.2.1), (6.2.2). Необходимым условием существования вещественной бифуркации является требование, чтобы линеаризованное уравнение

df(z, у, у', а) df{z,y у', а) (g gд/ч

ду ду

С граничными условиями

аоб(0) + М'(0) = 0, ai6(l)-f 6i6(l) = 0 (6.3.18)

имело ненулевое рещение. Если такое решение 6(2) существует, то cb{z) также будет решением. Чтобы выделить одно конкретное решение, нужно некое условие нормировки. Одна из возможностей заключается в том, чтобы выбрать

б(0)=1 (6.3.19)

Г == л/Re {hF + Hf) + Re {2Ff - 2Gg + 1), (6.3.21 a)

= 2 Re {Fg + fG) -f VR(/ + Gh), (6.3.21b)

/i = -2VRe /. (6.3.21c)

A(0) = f(0) = /i(l) = f(l) = gr(0) = 0, g(l) = S{k). (6.3.21d)

В точке поворота (по параметру S) должно быть

-§- = 0, т. е. g{l) = 0. (6.3.22)

Таким образом мы получаем систему шести дифференциальных уравнений (Р17-16), (Р17-17), (Р17-18), (6.3.21а), (6.3.21Ь), (6.3.21с) (имеющую суммарно десятый порядок) и двенадцать граничных условий (Р17-19), (Р17-20), (6.3.21d), (6.3.22). На

Напомним, что в этой задаче: а) искомыми являются функции Р{г). 0(г), Я(г) и число С; б) в уравнение (Р17-16)-(Р17-18) входят два (безразмерных) параметра - число Рейнольдса Re и отношение угловых скоростей дисков S. Зафиксируем Re н будем искать точку поворота по параметру S. При приближении S к критическому значению S* к' (S) ~

1о о. г-1/2 Г дР до дН\

-~ I S - S I оо (аналогично ведут себя -gg-J

Для S, близких к S*, примем за параметр k и положим S = S{k), Р - F(z,k) ... . - Прим. ред.

В случае, когда bo ф 0. (Если bo = О, то можно положить <5(0)=1.) Уравнения (6.2.1), (6.3.17) вместе с граничными условиями (6.2.2), (6.3.18), (6.3.19) представляют собой нелинейную краевую задачу, число условий в которой на единицу превышает порядок системы. Это, однако, компенсируется тем, что параметр а мы рассматриваем в качестве неизвестной; решив краевую задачу, мы получим значение а, отвечающее вещественной бифуркации. Замена данной задачи соответствующими разностными формулами приводит к системе нелинейных (алгебраических) уравнений с почти ленточной схемой размещения (ленточный характер матрицы нарушает столбец, который соответствует неизвестной а). Результаты так проведенных расчетов для задачи 16 представлены в работе [6.10].

Другую возможность применения разностных методов можно продемонстрировать при нахождении точек поворота в задаче 17 Введем следующие обозначения:

i дР да , дН , -

f-dk ё = = (6.3.20)

Продифференцировав уравнения (Р17-16) - (Р17-18) по переменной k, найдем

первый взгляд задача переопределена; на самом деле это не так, поскольку кроме f{z), g{z), h{z) ищутся значения двух неизвестных k и S.

Для решения указанной нелинейной краевой задачи использовались стандартные разностные замены на сетке с узламр* Zi = ih, г = О, 1, п, h=\/n (аналогичные заменам вида

-0,5 0,0 0,5 5

Рис. 6.11. Бифуркационная диаграмма задачи 17.

(6.1.23)). В частности, уравнению (6.3.21Ь) отвечает разностная система

g< + I - g£-I

+ VRe

2й

-Yh-

я уравнению (6.3.21c)-соотношения вида h, - h,

-bi = VRr(f;+fi-i), г=1, 2. n.

Если ввести вектор неизвестных величин Х = (Яо, Ло, Fr; fo. Go, go, Hi, hi, Fl, ...

.... я , fn, Gn, gn, k, S) (6.3.23)

и подходящим образом упорядочить разностные уравнения, то мы получим систему 6(п-1)-1-2 нелинейных уравнений

Ф(Х) = 0 (6.3.24)

с матрицей размещения, близкой к 15-диагональной. Для решения системы (6.3.24) можно снова воспользоваться методом

TO, в соответствии с п. 5.4.1, необходимым условием вещественной бифуркации будет выполнение соотношения

Fz Л2, L) = det J (n, L) = О . (6.3.26)

Преимуществом метода стрельбы является то обстоятельство, что бифуркационное условие (6.3.26) записывается в пространстве меньшей размерности. Используя теперь формулу (6.1.29), перепишем (6.3.26) в виде

Р,{щ, L) = p,il)py,il)-p,{l)py,(l) = 0. (6.3.27)

Точно так же, как и в п. 5.4.1, мы будем рассматривать уравнения (6.2.32), (6.3.27) как систему трех нелинейных уравне-лий относительно трех неизвестных r\i, г]2 и L ( координат точки вещественной бифуркации). Для решения этой системы

Действительно, если J = О, то существует ненулевое решение <(р, линеаризованной задачи:

, , дх , . дх ду , . ди

- Прим. ред.

Ньютона, а для решения систем линейных уравнений на каждой итерации использовать специальные алгоритмы для структурированных матриц. Размерность решаемых задач оказывается достаточно большой.

На рис. 6.11 приведена бифуркационная диаграмма в плоскости параметров Re и S, построенная с помощью описанного выше подхода. Эта бифуркационная диаграмма не является полной. В некоторых ее областях указано число решений задачи 17 при соответствующих значениях параметров Re и S. На рис. 6.11 при Re = 625 легко найти все шесть точек поворота, указанных на рис. 6.2.

6.3.2.2. Метод стрельбы,

Опишем кратко этот метод на примере системы реакция - диффузия (6.1.1), (6.1.2) с граничными условиями типа 2, т. е. с условиями (6.1.4). Выбирая г\ в (6.1.24) и используя условия (6.1.4а), мы можем решить задачу Коши для уравнений (6.1.1), (6.1.2) на промежутке от точки 2 = О до точки 2=1, где нам нужно удовлетворить условию (6.1.4Ь), т. е. соотношению (6.2.32). Если ввести матрицу Якоби

J(r L) = rl, (6.3.25)

МОЖНО воспользоваться, например, методом Ньютона. Матрица Якоби для метода Ньютона вычисляется следующим образом. Из соотношений (6.1.29), (6.2.37) найдем значения производных dFi/дци dFi/dt\2, dFi/dL, i = 1, 2. Производные для i= 3 можно получить, либо используя разностные формулы, либо с помощью вариационных переменных второго порядка

РхЦ - Лг, Лг, PxiL

Pyil

Дифференцируя уравнения в вариациях (6.1.27) по ци Лг и L, можно получить дифференциальные уравнения для этих переменных и соответствующие начальные условия.

дц. дГ д^у

Рис. 6.12. Бифуркационная диаграмма для задачи 14; у = 20, Рем = 10, Рен = 5, В = 15, вс = 0. В отдельных областях указано число решений.

Для нахождения точки ветвления (см. п. 5.4.1) потребуем, помимо выполнения соотношений (6.2.32), (6.3.27), чтобы было выполнено также уравнение

F,{n, л„ L) = detQ(n, L) = р',(1)р',(1)-

-p;i.(l)P;,(l) = 0, (6.3.28)

где матрица G получается из матрицы (6.2.33) вычеркиванием среднего столбца. Для решения системы четырех уравнений