aril aria dL

a/2 dFi dFi

aril atia dL

(6.2.33)

используем вариационные переменные pxi, pyi, определяемые соотношениями (6.1.26) - (6.1.28), a также переменные

PxL = dx/dL, Py[ = dyldL, (6.2.34)

для которых нетрудно получить следующие уравнения в вариациях:

pU+(p-.+%p..)+-.y)= *

с начальными условиями

PxL (0) = PxL (0) = PyL (0) = PyL (0) = 0. (6.2.36)

втором -имела место противоположная ситуация. В первом случае мы решаем уравнения (6.2.9), (6.2.10) при фиксированном (предсказанном) значении параметра а; во втором случае-при фиксированном (предсказанном) значении Уо = у{0), а параметр а считается неизвестным. Блок-схему предложенного алгоритма продолжения типа предиктор-корректор читатель легко может построить самостоятельно.

6.2.3.2. Алгоритм, основанный на методе стрельбы

Идею этого метода мы теперь продемонстрируем на примере задачи (6.1.1), (6.1.2) с граничными условиями (6.1.4). Зададим снова два недостающих начальных условия в точке г = О (см. (6.1.24)): x(0)=Tii, г/(0) =112. Интегрируя уравнения (6.1.1), (6.1.2) с начальными условиями (6.1.4а), (6.1.24) при некотором значении параметра L, мы должны получить в точке z= 1

Л (ill. гь, L) = xil, 1\, L) = 0, Fini, T2, L) = yil, r\, L) = 0.

(6.2.32)

Таким образом, у нас имеются два уравнения относительно трех неизвестных tii, ti2, L. Для нахождения соответствующей кривой в пространстве {ц1,х\2,Ц мы можем использовать алгоритм DERPAR, описанный в § 5.2. Для вычисления матрицы Якоби

г dFi dFi dF, -,

(6.2.39)

где квадратные скобки означают целую часть заключенного в них отношения. Если теперь взять все известные ветви элементарных решений, то общее число различных решений для

Частные производные в уравнении (6.2.33) задаются формулами (6.1.29), а также соотношениями

f = P;.(l)- (6-2.37)

Таким образом, мы имеем все необходимое для использования алгоритма продолжения DERPAR (см. п. 5.2.3): можем вычислить функции Fl и Fi по формулам (6.2.32), а также матрицу Якоби (6.2.33). Для одного такого вычисления нам необходимо решить задачу Коши для восьми дифференциальных уравнений второго порядка (6.1.1), (6.1.2), (6.1.27) и (6.2.35), т. е. для системы 16-го порядка.

В случае ГУ1 алгоритм изменяется в соответствии с формулами (6.1.30), (6.1.31), (6.1.32); при этом частные производные, входящие в матрицу Якоби (6.2.33), имеют вид

flF ЯР ЯР (6-2.38)

= P l(l), -QPyiil), = P,t(l).

Приведенный подход, основанный на методе стрельбы и вариационных дифференциальных уравнениях, называется в литературе методом GPM [6.8, 6.13, 6.14].

Диаграмма решений, найденная с помощью метода стрельбы и алгоритма продолжения DERPAR для задачи 11 в случае ГУ2, представлена на рис. 6.3 [6.15]. Здесь же приведены решения, полученные с помощью суммирования (профилей) решений (см. формулу (4.3.17)). Для некоторых ветвей указана устойчивость соответствующих решений. Из рисунка видно, что при больших L существует значительное число различных стационарных решений. Попробуем оценить это число. Рассмотрим ветвь элементарных решений, т. е. решений, которые не могут быть получены путем сложения решений с меньшими L. Пусть такая ветвь существует при (L,-, Li-fAL;). Если мы выберем максимально широкие промежутки существования, то тогда Li и Li -f AL; представляют собой координаты точек бифуркации. Фиксируем теперь длину L и исследуем, сколько различных решений, полученных сложением из решений этой ветви, будет существовать для такого L. Это число равняется разности

ДЛИНЫ L будет равно

(6.2.40)

где единица представляет собой (при всех L) существующее тривиальное решение х = Л, у^В/А. Эти рассуждения остаются справедливыми для любых систем типа реакция-диффузия с граничными условиями типа ГУ2. Если нам известны не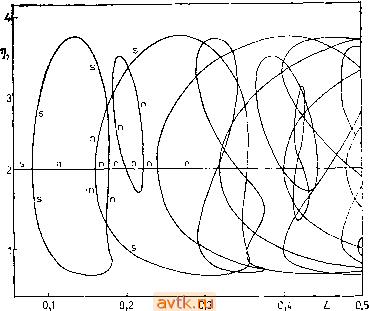

Рис. 6.3. Диаграмма стационарных решений для задачи 11 при ГУ2, А = 2, iS = 4,6, = 0,0016, Dy = 0,008, т), =л:(0); s - устойчивые, п ~ неустойчивые решения.

все ветви элементарных решений, то тогда выражение (6.2.40) дает нижнюю оценку числа решений для данного L. Так, при L = 1 на основании рис. 6.3 мы находим, что существует минимум 35 стационарных решений задачи 11 для случая ГУ2 (см. табл. 6.8 с учетом того, что существуют еще тривиальные решения задачи (при любых L)).

Пример диаграммы стационарных решений для задачи И в случае ГУ1 представлен иа рис. 6.4, а более полную картину решений наряду с профилями x{z), y(z) читатель может найти в [6.15]. У некоторых ветвей на рис. 6.4 указан характер их

Таблица 6.8. Число Ni стационарных решений задачи 11 для случая ГУ2 (Z, = 1), полученных М,-кратным сложением элементарных решений при L = Z.,., Л = 2, iS = 4,6, Dx = 0,0016, Dy = 0,008.

устойчивости. Отметим также, что операция сложения решений в случае ГУ1 оказывается невозможной.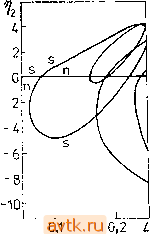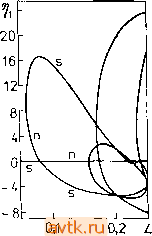

Рис. 6.4. Диаграмма решений для задачи ,11 при ГУ1, А = 2, В = 4,6, D = = 0,0016, Оу = 0,008, r\i = x(Q), г\2 = у'(0); s - устойчивые, п -неустойчивые решения.

Часть диаграммы решений для задачи 12 в случае ГУ2, содержащая только элементарные решения, представлена на рис. 6.5. При выбранных параметрах задача имеет три тривиальных решения (они указаны в описании к рисунку, так что читатель может сравнить эти данные с данными рис. 5.6b и 5.20е). Точно так же, как и в случае рис. 6.3, мы можем под-

считать число решений при больших L, полученных путем сложения элементарных решений. Диаграммы решений с использованием условий типа ГУ1 представлены на рис. 6.6 для случая граничных условий, определяемых тривиальным решением № 3, указанным в описании к рис. 6.5.

На рис. 6.7 изображена диаграмма решений задачи 13 в случае граничных условий ГУ2. Здесь же частично представлены решения, полученные сложением решений, и указан характер устойчивости отдельных ветвей.

L 0,4

Рис. 6.5. Диаграмма решений для задачи 12 при ГУ2, а = 12, р = 1,5, у = = 3, 6=1, Vo = 0,01, Ох = 0,008, Оу = 0,004; r\i = x{0), tja = (/(0).

Тривиальные решения в системе без пространственных градиентов (Од = = £>У = 0):

Покажем теперь, как изменится схема алгоритма в случае задачи 14. Будем искать зависимость решения уравнений (6.1.35а,Ь) с граничными условиями (6.1.36а,Ь) от параметра Da. Выберем два недостающих начальных условия в форме (6.1.37) и положим в точке 2 = 0

f,(Tj, Da) = Pe i/(0)-r/(0) = 0,

F, (т1. Da) = Ренв (0) - в' (0) = 0.

Вариационные уравнения для переменных Ру\=ду/дх\х, pyi = = ду/дц2, pyD!L=dy/dDa, pei=de/dr\u рв2 = дв/дг\2, Peca = = (?0/(?Da читатель может легко получить дифференцированием уравнений (6.1.35а, Ь) по rji, TI2 и Da. Начальные условия

20 М.. Холодннок и др.

0,3 0,4 0,5 L 0,6

Рис. 6.6. Диаграмма решений для задачи 12 при ГУ]. х = 0,7006, у = 3,5106;, т)1 = х'{0), 1)2 = у'(0)- Остальные параметры указаны на рис. 6.5; s -устойчивые, п - неустойчивые решения.

ДЛЯ НИХ выбираются нулевыми, кроме условий pyi(l)=l, Рв2(1)=1. При этом матрица Якоби системы (6.2.41) будет иметь вид

РемР (0)-р;,(0), РеРуЛ0)-Ру2{0\ Р^,лРуиЛ^) - РувЛ)

.РенРв1(0)-Рж(0). РенРе2(0)-р;2(0). Р^нРвиЛ^)-РепАО) /

(6.2.42)

Диаграмма стационарных решений, полученная этим методом'\ приведена на рис. 6.8. При Da = О начальную точку зависимости можно найти аналитически. Сравните число решений для различных значений параметра Da, приведенных в табл. 6.4 и 6.5.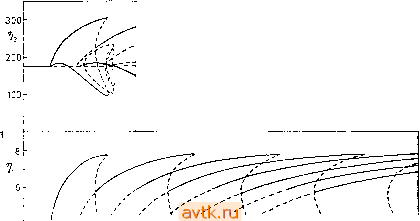

2г

Рис. 6.7. Диаграмма решений для задачи 13 при ГУ2; ц = 0,0035, v = 6-10-<, с = 0,05, с' = 0,025, р = р' = 3,2, = 0,01, Оу = О = л:(0), т)2=1/(0); сплошные линии - устойчивые, прерывистые

чивые решения.

= 0,0045, 45, т)! = - неустой-

В заключение этого пункта проиллюстрируем, как найти зависимость решения от параметра в случае задачи 15. Здесь годится подход, вполне аналогичный тому, который использовался нами в задаче 14 (в чем, впрочем, мы могли убедиться еще в предыдущем параграфе).Итак, будем искать зависимость решения уравнений (Р15-6), (Р15-7) совместно с нелинейными (алгебраическими) уравнениями (Р15-8), (Р15-9) от параметра Da. Граничные условия вновь имеют форму (6.1.36а,Ь). Два яедостающих начальных условия в точке 2=1 выбираем в

> То есть применением алгоритма DERPAR к нахождению кривой -fi(T)i, т)2, Da) = Рг(ц1, г\2. Da) = О. - Прим. ред.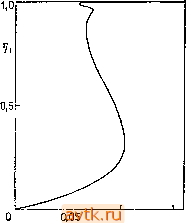

0,10 Da 0.15

0,05

0,10 Da 0,15

Рис. 6.8. Диаграмма решений для задачи 14. Рем = 10, Рен = 5, В = 15, Р = 2, вс = 0, Y = 20, Т1, = j,(l), т1г=в(1).

Рис. 6.9. Диаграмма решений задачи 15. Зависимость температуры иа выходе 12 = в(1) от параметра Da. Рем = 20, Рен =10, 6=1, В = 10, у = 20,

в, = О, /м = /и = 25.

соответствии с формулами (6.1.37), а в точке 2 = О имеем два нелинейных уравнения вида (6.2.41). Вариационное уравнение для Ру1 имеет вид (6.1.40). Вариационные уравнения для остальных переменных (6.1.39), а также для переменных pyDa = dy/dDa., реоа =dQ/dDa. выводятся аналогично. При этом матрица системы (6.2.41) имеет вид (6.2.42).

Напомним, что на каждом шаге иитегрироваиия уравнений (Р15-6), (Р15-7), а также соответствующих вариационных уравнений иам необходимо вычислять значения переменных (6.1.41) т. е. переменных дса/ду, dca/dQ, dQ/dy, dQ/d&. Эти значения мы находим по формулам (6.1.43) так же, как это делалось в § 6.1.

На рис. 6.9 приведена диаграмма решений рассматриваемой задачи в зависимости от параметра Da. Как видио из рисунка в узком интервале значений параметра данная задача имеет 5 решений. Для указанных значений параметров уравнение (Р15-11) имело только одно решение о в промежутке [y{z), 1] при любом [О, 1].

Построение диаграммы решений несколько осложняется в тех случаях, когда уравнение (Р15-11) имеет несколько корней. Подробный анализ задачи 15 читатель может иайти в сборнике [6.16].

6.2.4. Метод отображения параметра

В некоторых случаях оказывается возможным достаточно, быстро построить диаграмму стационарных решений, если к выбранному значению некоторого начального условия с помощьк> интегрирования задачи Коши мы добавим соответствующее значение параметра. Аналогичный подход был описай для сосредоточенных систем в п. 5.2.1. Так же, как и там, возможность применения этого подхода зависит от конкретного вида дифференциальных уравнений и граничных условий, а также or того, как входит в уравнения выбранный параметр. Поэтому мы продемонстрируем применение указанного метода иа двух конкретных задачах из гл. 4. Более общие соображения читатель может иайти в книгах [6.8, 6.9] и в приведенной в них библиографии.

Будем строить зависимость решения задачи 16 от параметра Ф. Для стационарного случая мы свели эту задачу к одному дифференциальному уравнению второго порядка (6.1.21) с граничными условиями (6.1.16а,с). Введем новую независимую переменную

2 = Фг. (6.2.43>

Тогда дифференциальное уравнение (6.1.21) приведется к виду

т. е. не будет содержать Ф.

Граничные условия приобретут вид

2 = 0:-g- = 0, (6.2.45а)

2 = Ф: у=\. (6.2.45Ь)

Выберем теперь недостающее начальное условие в виде

г/ (0) = л, О < л < 1 (6.2.46)

л проинтегрируем полученную задачу Коши (6.2.44), (6.2.45а), (6.2.46) от 2 = О до точки 2 = 2i, в которой

i/(zi) = l. (6.2.47)

Значение Z\ определяет значение параметра Ф, соответствующее выбранному начальному условию л (и найденному решению

2i = Ф. (6.2.48)

Для выполнения равенства (6.2.47) можно воспользоваться каким-либо методом последовательных приближений, например методом деления промежутка пополам. Процесс можно, например, реализовать так. Когда в процессе интегрирования становится у{г)> 1, мы возвращаемся на один шаг назад и продолжаем интегрирование с более коротким шагом (например, уменьшенным вдвое). По достижении достаточно короткого шага процесс прекращается.

Опишем коротко неитерационный способ нахождения величины 21. Проинтегрируем уравнение (6.2.44), переписав его в виде системы двух дифференциальных уравнений первого порядка,

dy dw а . yP(1-v) if п ап\

= j/expYp(i-%) (6.2.49)

с начальными условиями (6.2.45а), (6.2.46), т. е. с условиями г/(0) = л, ш(0) = 0. В некоторой точке 2 > О, где y{z) = y<l и dy/dz = g, мы переходим к интегрированию дифференциальных уравнений вида

dw а , У уР(1 - у) dz I /с о спч

dy - Т + Р 1 + (1-у) Ч^- (6.2.50)