а рис. 2.14 диаграмму, которую будем называть диаграммой (стационарных) решений уравнения (2.2.1). Точки параболы а, - -х^ изображают состояния равновесия уравнения (2.2.1). Верхняя ветвь параболы представляет собой ветвь неустойчивых положений равновесия, нижняя ветвь - устойчивых.

В случае реальной системы, описываемой уравнением (2.2.1), система стабилизируется в устойчивом состоянии равновесия, так что о существовании другого, неустойчивого состояния равновесия мы, как правило, ничего не знаем. При переходе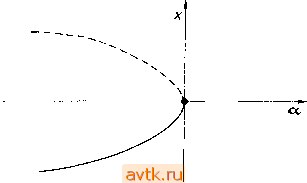

Рис. 2.14. Диаграмма стационарных решений уравнения (2.2.1).

параметра а через бифуркационное значение а = 0 слева направо это устойчивое состояние равновесия внезапно исчезает. Наоборот, если параметр а переходит через бифуркационное значение а = 0 справа налево, то в этом случае у нас внезапно появляется одно устойчивое состояние равновесия системы. Замечание 2.3. Линеаризуя уравнение (2.2.1) в окрестности

положений равновесия >;i(a) = -Vlal и д;2(а) =-}-1 о|> получаем

2 = -2 W\Z и ; z = 2 д/Ыz. (2.2.2)

Поскольку уравнение (2.2.1) является одномерным, обе матрицы линеаризации имеют порядок 1 и их собственные числа

равны соответственно Я,(а) = -2Va и A,2(a) = 2Vla> причем

lim Я, (а)= lim A,2(a) = 0. (2.2.3)

а- --о а- --О

Матрица линеаризации в состоянии равновесия х = 0 (соответствующем бифуркационному значению параметра а = 0) имеет нулевое собственное число.

В общем, -мерном случае, если для некоторого положения равновесия матрица линеаризации имеет одно собственное число, равное нулю, бифуркация происходит аналогично: при изменении параметра положение равновесия либо исчезает, либо расщепляется на два новых положения равновесия. Можно доказать, что это утверждение справедливо для почти всех 1-па-раметрических систем дифференциальных уравнений с -мерным фазовым пространством.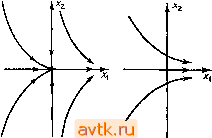

а.<0 С1=0 О(,>0

Рис. 2.15. Бифуркация типа седло - узел для 1-параметрической системы X[ = д:, Ч- а. Х2 = - Хо.

На рис. 2.15 изображена бифуркация типа седло-узел для двумерного случая. Из рис. 2.15 видно, что при а<0 система имеет два положения равновесия, одно из которых есть седло, а другое - узел. Эти точки при а- -О приближаются друг к другу и при а = О сливаются вместе в так называемое седло-узел . Отсюда и возникло название бифуркация типа седло-узел .

2.2.2. Бифуркации Андронова - Хопфа

Начнем снова с простейшего примера - рассмотрим бифуркацию положения равновесия для следующей 1-параметрической системы двух дифференциальных уравнений:

Х2 = х^ + ах~х^ {х\ + х1).

d dt

(2.2.4)

Система (2.2.4) имеет положение равновесия л: = (0,0) при любых значениях параметра а. Исследуем его устойчивость при различных значениях aeR.

(2.2.5)

она имеет комплексные собственные числа

А ,2(а) = а±г. (2.2.6)

Следовательно, при а <: О состояние равновесия х = (0,0) представляет собой устойчивый фокус, а при а > О - неустойчивый фокус. При а = 0 собственные числа располагаются на мнимой оси, и об устойчивости состояния равновесия нельзя судить по линеаризованной системе.

Для исследования фазового портрета системы (2.2.4) удобно преобразовать ее к полярным координатам. Положим

Х| = г cos ф, Ха = г sin ф (2.2.7)

и продифференцируем левые и правые части соотношений (2.2.7) по времени, считая переменные г и ф функциями t. Мы получим

х, = г COS ф - гф sin ф,

. . . , (2.2.8)

Ха = г sin ф-(-Гф COS ф.

После подстановки в уравнения (2.2.4) и простых преобразований получаем систему

г = г (а - г2), (2.2.9)

.ф=1. (2.2.10)

Из второго уравнения следует, что переменная ф играет роль времени (ф = /--/о) и что наиболее существенная информация о структуре траекторий содержится в уравнении (2.2.9).

Положения равновесия уравнения (2.2.9) суть решения уравнения

г(а-г2) = 0; г>0. (2.2.11)

Таким образом, одно положение равновесия г] = О существует при любых значениях параметра а. При а О других положений равновесия нет.

При а > О уравнение (2.2.9) имеет еще одно состояние равновесия Vo > которое является устойчивым.

Положение равновесия ri=0 уравнения (2.2.9) отвечает положению равновесия х = (ОЛ)) системы (2.2.4), тогда как положение равновесия Г2= соответствует устойчивой замкну-

3 М. Холодннок н др.

Матрица линеаризованной системы в точке х = (Q, 0) имеет

вид

-а, -11 .1, аУ

ТОЙ траектории системы (2.2.4), а именно окружности радиуса Va-

Таким образом, при переходе параметра а через нуль слева направо устойчивый фокус становится неустойчивым, и от него отделяется замкнутая траектория, диаметр которой растет пропорционально величине Va-

Такое явление называется бифуркацией Андронова-Хопфа (или бифуркацией рождения цикла); схема его изображена на рис. 2.16.

Бифуркация Андронова-Хопфа устанавливает связь между потерей устойчивости положений равновесия и возникновением периодических решений в системах дифференциальных уравнений.

В реальных системах бифуркация Андронова-Хопфа возникает довольно часто. В приложениях удобно наглядно представлять бифуркацию Андронова-Хопфа, изображая графически зависимость отдельных фазовых переменных от времени (см. рис. 2.17, который соответствует рис. 2.16). В экспериментах при значениях параметра, близких к критическому, возникающее периодическое решение мало отличается от стационарного решения, поскольку его амплитуда очень мала и ,может теряться в экспериментальном шуме.

Пример 2.7. Процесс бифуркации для 1-параметрической системы дифференциальных уравнений вида

х,х,+ах, + х,{х] + х1) --

изображен на рис. 2.18. Возникающая здесь замкнутая траектория является неустойчивой.

Про бифуркацию Андронова-Хопфа, происходящую по сценарию рис. 2.16, говорят, что в этом случае происходит мягкая потеря устойчивости положения равновесия. Здесь система под действием постоянно присутствующих малых возмущений переходит сначала из неустойчивого состояния равновесия на малую устойчивую периодическую траекторию, так что изменение поведения системы оказывается постепенным, мягким . Другая возможность изображена на рис. 2.18. Здесь с возрастанием параметра область притяжения устойчивого фокуса (и амплитуда неустойчивого периодического решения) уменьшается, и при исчезновении периодической траектории положение равновесия становится неустойчивым. Из него система под действием малого возмущения переходит в некоторый более отдаленный стационарный режим (часто--периодический) и, следовательно.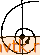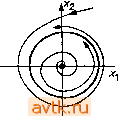

О1. = 0

Рнс. 2.16. Бифуркация Андронова-Хопфа (случай мягкой потери устойчивости) .

ot<Q

01=0

Рнс. 2.17. Бифуркация Андронова-Хопфа: временная зависимость для одной

йз переменных.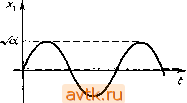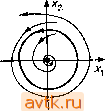

ct=0

Рис. 2.18. Бифуркация Андронова-Хопфа (случай жесткой потери устойчивости) .

при малом изменении параметра (в окрестности его бифуркационного значения) происходит сильное изменение состояния системы. Это явление называется жесткой потерей устойчивости.

Достаточные условия возникновения бифуркации Андронова-Хопфа в 1-параметрической n-мерной системе дифференциальных уравнений даются следующей теоремой. Теорема (Хопфа). Пусть система

x = f(x, а), xeR , aeR (2.2.13)

имеет положение равновесия х = О при любых значениях параметра а. Далее, пусть матрица линеаризации при значениях а в некоторой окрестности ао имеет пару комплексно сопряженных собственных чисел Xi,z{a,) =?( ) ±гсо(а), причем

g(ao) = Q, a)(ao) = a)o>Q. §;(щ)ФО.

Кроме того, предположим, что остальные п - 2 собственных чисел имеют ненулевые вещественные части.

Тогда прн а = ао от нулевого положения равновесия ответвляется однопараметрическая система замкнутых траекторий, отвечающих периодическим решениям периода Г(а) 2я/©о, (7(а)- -2я/й)о при а->-ао. - Ред.). Замкнутые траектории могут ответвляться либо при а < ао, либо при а > ао.

2.2.3. Бифуркации при наличии симметрии

Если дифференциальные уравнения описывают реальный процесс, обладающий некой симметрией, то эта симметрия проявится в дифференциальных уравнениях и тем самым окажет влияние на бифуркации.

Пример 2.8. Рассмотрим 1-параметрическое дифференциальное уравнение

x = f{x, а), xR,

правая часть которого удовлетворяет соотношению f{-x,a,) = = -f(x,a), т. е. функция f является нечетной по переменной х. Чтобы понять, что дает такой вид симметрии, выберем простейший вид /, f(x,a) = ax - х^, и исследуем бифуркационные явления в полученном уравнении

х = ах-х\ (2.2.14)

Положение равновесия найдем, решая уравнение

ax - x = Q,

Т. е. л:( == О - состояние равновесия при любых а е R и х^= = ±V при а > 0. Таким образом, уравнение (2.2.14) при а О имеет одно устойчивое положение равновесия Xi = 0. При а > О это состояние равновесия становится неустойчивым, и от него ответвляются два устойчивых состояния равновесия х(2> = -у/а, х' = - V - Соответствующие портреты показаны на

cx<Q о<,= 0 ct>0

Рис. 2.19. Фазовые портреты уравнения (2.2.14).

рис. 2.19, а диаграмма стационарных решений уравнения (2.2.14) представлена на рис. 2.20. Учитывая форму этой диаграммы, описанную бифуркацию называют иногда бифуркацией типа вилки. Случай, описанный в примере 2.8, можно

Рис. 2.20. Диаграмма стационарных решений - бифуркация типа вилка .

включить в более общее рассмотрение дифференциальных уравнений с симметрией. Дадим формальное определение.

Рассмотрим векторное дифференциальное уравнение (систему)

x = f(x), xeR (2.2.15)

и пусть (р(/, х)-его фазовый поток. Если существует диффеоморфизм g:R ->R , такой, что для всех xeR имеет место соотношение

f(g(x)) = -f(x), (2.2.16)

Менее формальное определение. Уравнение х = f(x) g-инварнантно, если при замене переменных y = g(x) оно не изменяется (т.е. получается

y = f(y)). В частности, если х = p(/) - решение, то х = g (<р(/)) - тоже решение. - Прим. ред.

то МЫ говорим, что дифференциальное уравнение (2.2.15) инвариантно по отношению к диффеоморфизму g или, кратко, g-инвариантно. Диффеоморфизм g мы называем симметрией уравнения (2.2.15), а о самом дифференциальном уравнении говорим как о дифференциальном уравнении с симметрией

Если теперь мы имеем -параметрическую систему дифференциальных уравнений

x = f(x, а), xeR , aeR*, (2.2.17)

g-инвариантную для каждого а, то мы говорим, что система (2.2.17) представляет собой -параметрическую систему дифференциальных уравнений с симметрией g.

Пример 2.9. Рассмотрим 1-параметрическую систему (2.2.17) при п=1 и положим g{x)=-X. Формула (2.2.16) в этом случае принимает вид /(-х,а) = -f(x,a). Уравнение х = = f(x,a) g-инвариантно, если функция f(x,a) нечетна по переменной х (ср. с примером 2.8).

Для фазового потока <р уравнения (2.2.15) с симметрией g при любых / е R и xR имеет место соотношение

f(t. g(x)) = g(q)( X)). (2.2.18)

Следствие из формулы (2.2.18):

Если у есть траектория уравнения (2.2.15), го g(7) также является траекторией уравнения (2.2.15).

В частности, это утверждение справедливо и для положений равновесия, fi этом, собственно, и заключается сущность бифуркации типа вилки, описанной в примере 2.8: с отщеплением состояния равновесия х = \/а от нулевого состояния равновесия появляется также симметричное ему положение равновесия

g(Va ) = - Va-

Решение g-инвариантного дифференциального уравнения, траектория которого 7 удовлетворяет соотношению

g(Y) = Y.

называется симметричным решением.

В примере 2.8 симметричным решением является стационарное решение, соответствующее нулевому положению равновесия (x(t) = 0).

Обратимся вновь к рис. 2.20. Если двигаться в направлении возрастания параметра а, то в точке а = О происходит каче-

ственное изменение характера симметрии стационарных решений. При а < О устойчивое стационарное решение является -симметричным, в то время как при а > О соответствующее устойчивое стационарное решение этим свойством уже не обладает.

Таким образом, речь здесь идет о потере симметрии устойчивых решений при бифуркации (английский термин sym-metry breakings). Это явление возникает, к примеру, в хорошо известной модели Лоренца (см. задачу 10).

Уравнения Лоренца

х = а{у - х), у = -у + гх - XZ, Z == -bz -f ху

как легко проверить, инвариантны по отношению к линейному отображению 1

g(x, у, z) = {~x, -у, Z).

2.3. БИФУРКАЦИИ ПЕРИОДИЧЕСКИХ РЕШЕНИИ

В этом параграфе мы познакомимся с основными типами бифуркаций периодических решений систем дифференциальных уравнений; траектории этих решений - замкнутые кривые.

Рис. 2.21. Орбитальная устойчивость замкнутой траектории.

Изложение будет вестись последовательно на трех уровнях. В п. 2.3.1 мы на иллюстративном материале познакомимся с отдельными видами бифуркаций. В п. 2.3.2 для описания этих

бифуркаций мы используем отображение Пуанкаре, которое будет применяться также во многих случаях в главах 5 и 6. Наконец, в п. 2.3.3 и в последующих пунктах мы рассмотрим теоретическую аргументацию, на которой основаны численные методы исследования устойчивости периодических решений.

Замечание. Как и в случае положений равновесия, изменение характера устойчивости замкнутой траектории сопровождается бифуркацией. Строгое определение (орбитальной) устойчивости замкнутой траектории будет приведено в п. 2.3.3.

Пока же достаточно понимать, что замкнутая траектория у является устойчивой, если все траектории, достаточно близкие к траектории у, с возрастанием времени неограниченно приближаются к ней (см. рис. 2.21).

2.3.1. Основные типы бифуркаций периодических решений 1

Рассмотрим 1-параметрическую систему дифференциальных уравнений

x==f(x, а), aeR, х е R , (2.3.1)

которая при определенных значениях параметра а имеет замкнутую траекторию yi. В общем случае изменение значений параметра может послужить причиной одной из следующих бифуркаций.

скос* a.=c5t* ,> ,*

Рис. 2.22. Бифуркация рождения-исчезновения пары замкнутых траекторий.

(I). В фазовом пространстве системы (2.3.1) существует пара замкнутых траекторий уь 72, которые при изменении (например, при возрастании) параметра а сближаются друг с другом, при бифуркационном значении параметра а = а* сливаются вместе, а при дальнейшем изменении параметра исчезают (см. рис. 2.22). Если двигаться по рис. 2.22 справа налево, т. е. в направлении убывания параметра, то описываемая бифуркация представляется нам так, что при а = а* возникает