6.2. ЗАВИСИМОСТЬ СТАЦИОНАРНЫХ РЕШЕНИЙ ОТ ПАРАМЕТРА

Так же как и для сосредоточенных систем (описываемых обыкновенными дифференциальными уравнениями, см. § 5.2),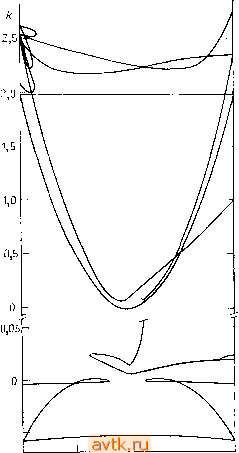

-1,0 -0,5 0,0 0,5 <У 1,0

Рис. 6.2. Диаграмма стационарных решений задачи 17, Re = 625.

существует целый ряд методов и подходов, позволяющих находить зависимость стационарных решений от параметров в случае распределенных систем, описываемых уравнениями

6.2.1. Метод дифференцирования по параметру

Рассматриваемая здесь методика аналогична описанной в п. 5.2.2 для конечномерных задач. Продемонстрируем здесь одну из возможных численных реализаций этого метода на примере продолжения по параметру а решения краевой задачи для (одного) дифференциального уравнения второго порядка ( = = d/dz)

y -f(z,y,y,a) = Q (6.2.1)

С частными производными. Набор методов оказывается здесь даже более широким, поскольку здесь есть еще и проблема аппроксимации задачи в бесконечномерном пространстве посредством задачи в пространстве конечной размерности.

Наиболее простым подходом является, конечно, последовательное использование какого-либо метода предыдущего параграфа для каждого значения параметра. Слова наиболее простым означают, что при этом мы не должны строить специальный алгоритм продолжения по параметру. Недостатком подобного подхода является, однако, необходимость осуществлять переходы через точки бифуркации с помощью вмешательства человека. В результате время, которое необходимо затратить в этом случае на диалог человек-машина , существенно возрастает. Иногда, тем не менее, предпочтение отдается именно этому подходу, особенно в случаях, когда нам нужно построить лишь небольшую совокупность решений (задан небольшой диапазон значений параметра) или же в случаях, когда частое появление бифуркационных значений параметра не ожидается.

Результаты последовательного использования метода Ньютона для системы разностных уравнений (6.1.23), которая возникает в задаче 17, представлены на диаграмме стационарных решений, показанной на рис. 6.2. В данном случае уже само решение системы (6.1.23) для больших п являлось достаточно серьезной проблемой.

В последующих пунктах мы рассмотрим методы продолжения по параметру стационарных решений для распределенных систем. Там, где это окажется более целесообразным, описание соответствующей методики будет проводиться на примерах конкретных задач из гл. 4.

Отметим, что методы, изложенные в п. 6.2.1 и 6.2.2, могут использоваться в качестве предиктора в схеме типа предиктор-корректор , описанной в п. 6.2.3, аналогично тому, как это делалось в § 5.2.

(6.2.4)

Предположим, что известно решение краевой задачи (6.2.1) - -(6.2.2) при а = ао

г/(2, ао) = ф(2). (6.2.5)

Дифференциальное уравнение в частных производных третьего порядка (6.2.3) можно решать разностными методами, аналогично простейшим уравнениям параболического типа (см. § 6.4). Выберем прямоугольную сетку узловых точек (г а,), .Zi = ih, г = 0,1, п; а/ = ао + /, / = 0,1, и обозначим ij\y(z,ay Простейшая разностная аппроксимация уравнения (6.2.3) с использованием шеститочечной схемы имеет вид

{у{1\ - 2уГ + уП\ -yUr + Ч - УЫ) ~ !ут(у1 -у1) -

- fyiyitl - yi-\-yU+ yU -~fa = 0, (6.2.6)

i=l, 2, n-l.

.Здесь fy, fy - соответствующие частные производные функции f, вычисленные, например, для значений переменных yi на /-м (уже найденном) слое : так,

Ту=-gfr--(6.2.7)

Используя подходящие разностные замены в граничных условиях (6.2.4) (см. п. 6.1.1 и § 6.4), мы получаем, вместе с соот-аошением (6.2.6), систему линейных алгебраических уравнений

<с граничными условиями

ад(0) + 6о/(0) = Со, (6.2.2а>

(1) +V(l) = ci. (6.2.2b)

Подставив в уравнение (6.2.1) y = y{z,a) и дифференцируя по а, мы получаем уравнение

д'у df ду df д'у df ,

dzda ду да ду дгда da {о.а.о)

граничными условиями вида

ад (О, а) + 6о^ = Со.

V 2 4А 2 /

(6.2.8)

В результате мы получаем систему нелинейных уравнений относительно неизвестных с верхним индексом j -\- 1, для решения которой можно использовать какой-либо итерационный метод например, метод Ньютона.

Уравнение (6.2.3) можно также аппроксимировать методом прямых (см. § 6.4). Более подробный анализ метода дифференцирования по параметру можно найти в книге [6.8].

Выше мы сначала проводили дифференцирование по параметру а, а затем решали задачу численно (дискретизировали ее). Обратный порядок действий также возможен. Так, сначала' мы можем преобразовать задачу (6.2.1), (6.2.2) с помощью соответствующих разностных формул, например, приводя ее к виду

f и. у., , ] - о, (6.2.9).

г = 0, 1, ..., п, ахУп + h {y +i - yn-\)l2h = с,.

(6.2.10>

Переменные г/ 1 и уп+\ можно найти из условий (6.2.10), а затем подставить их в уравнение (6.2.9). К полученной таким образом системе п-\- 1 нелинейных уравнений fi{yo,yi, уп)=0,. г = 0, 1, п можно затем применить метод п. 5.2.2. Интегрируя дифференциальные уравнения (5.2.8) методом Эйлера, мы получаем алгоритм, сходный с тем, который описывался выше.

Точно так же, как и в случае задач конечной размерности, здесь метод дифференцирования по параметру а не позволяет преодолевать точку поворота на диаграмме решений. Метод дифференцирования по длине дуги в том виде, как он был описан в п. 5.2.2, позволяет спокойно проходить точку поворота,.

относительно неизвестных г/+, г/{+, .... г/+ (переменные-с верхним индексом / нам известны). Матрица системы является трехдиагональной, и поэтому мы можем воспользоваться-алгоритмом исключения Гаусса, работающим только с ненулевыми элементами.

Поскольку разностная замена (6.2.6) центрирована относительно точки (г, /-1-1/2), то уменьшения погрешностей аппроксимации можно достичь, заменяя коэффициенты fy, f f в этой точке, т. е. вводя в соотношения (6.2.7) аргументы

хотя для задач типа (6.2.9) при большом п без преобразований, использующих специальные структуры матрицы Якоби, этот метод применять невозможно. Использование указанного метода удет обсуждаться ниже, в п. 6.2.3, а также в связи с методом дифференцирования по граничному условию (п. 6.2.2).

Продемонстрируем теперь применение метода дифференцирования по параметру на примере задачи 16. В предыдущем пункте мы вывели уравнение (6. .21), которое можно представить в виде (6.2.1), полагая z = r и а = Ф. Если теперь обозначить

(У) ехр ,

-то уравнение (6.2.3) для (6.1.21) принимает вид

+ -1 ф2

(1-f

2ФуЕ{у) = 0.

(6.2.11)

Храничные условия при Nu->oo, Sh->oo записываются как

(6.2.12)

= 0, ,(1,Ф)=1.

Начальное условие (6.2.5) легко получается аналитически в виде

Ф = 0: г/(г, 0)= 1. (6.2.13)

При этом разностная аппроксимация уравнения (6.2.11) проводилась в соответствии с формулами (6.2.6) и (6.2.7), а замена .граничного условия в точке г = О осуществлялась точно так же, как в уравнении (6.1.22Ь). Влияние выбора шагов сетки h и k иллюстрируется табл. 6.6. Заметим, что для получения значения г/(0, 1) при Л = 0,025 и = 0,002 нам пришлось 500 раз.

Таблица 6.6. Метод дифференцирования по параметру ф для задачи 16, а = О, у = 20, Р = 0,05. Приведены значения !/ (О, 1), т. е. значения концентрации в центре частицы при ф = 1 (точное значение равно 0,5521). Видно влияние шагов Л и fe.

решить систему 40 линейных алгебраических уравнений с трехдиагональной матрицей. Тем самым было найдено 500 точек на диаграмме, описывающей зависимость стационарного решения от параметра.

Применение метода дифференцирования по параметру мы продемонстрировали на примере одного уравнения второго порядка. Переход к системе таких уравнений также не представляет особых трудностей - при этом лишь увеличится размерность решаемых задач и вместо трехдиагональной мы будем иметь дело с ленточной матрицей. Читатель может легко вывести соответствующие уравнения в частных производных для задач И, 12, 13, 14. Задача 17 была решена этим методом в работе [6.12]. В следующем пункте описывается модификация данного метода, с помощью которой мы можем проходить точки, поворота на диаграмме стационарных решений.

6.2.2. Метод дифференцирования по граничному условию

Обратимся вновь к задаче (6.2.1), (6.2.2), предполагая, что* ЬоФО. В качестве нового параметра задачи введем значение решения в точке z = 0:

y{0) = t (6.2.14>

Решение у задачи (6.2.1), (6.2.2) будет зависеть от пространственной переменной z и параметра , т. е. y = y{z,l) Дифференцируя уравнение (6.2.1) по g, находим

д'у df ду df д^у df da /fi9,cv

azai dy dl dy dz dl da dl

Граничные условия (6.2.2) принимают вид

ад(0, 1)+ 6о- = Со, а,г/(1, )-bb,ilb = Cb (6.2.16а>

причем из формулы (6.2.14) следует, что

t/(0, ) = . (6.2.16Ь)

Теперь а есть функция от , и в уравнение (6.2.15) входит неизвестная величина

C = da/dt (6.2.17>

Поэтому три граничных условия (6.2.16) не делают задачу переопределенной. Начальное условие для продолжения по параметру мы задаем в форме

I = 1о: а = Оо, г/ (Z, 1о) = Ф (z), (6.2.18>

д^у а д^у .

drdl г drdl °

(1 + И1- /))Ч^( %

-уЕ{у) = 0. (6.2.21>

Граничные условия записываются в виде

MaL = o, у{\,1)=\, у(0,Ю = 1. (6.2.22)

тде функция ф{2) есть решение исходной краевой задачи (6.2.1), (6.2.2) при а = ао и ф(0) = о- В этом случае функцию ф(г) часто можно найти в аналитическом виде для некоторого промежуточного значения параметра а.

Дифференциальное уравнение в частных производных (6.2.15), точно так же, как и в предыдущем пункте, нетрудно аппроксимировать соответствующими разностными уравнениями. Обозначим 2,. =/А, / = 0, 1, п, % = 1, +jk, /=1, 2,

у [Zi, I.) у[, a{l,j)a., h=l/n. Тогда разностная аппроксимация уравнений (6.2.15) и (6.2.16) приводит к соотношениям

4-111+ %r + i+iy:l+C = ?[, / = 0, 1, п, (6.2.19а>

аоУ^ + К {У'Г - yiVVfi с„, (6.2.19Ь)

1- + {Уп1\ - ykt\)/2h=c (6.2.19с)

yt = li + k. (6.2.19d)

Коэффициенты sl-i, sl, sl+i, r\, q{ вычисляются с помощью известных значений решения иа предыдущем слое при = / (т. е. при а = а,). Соотношения (6.2.19) представляют собой систему п + 4 линейных алгебраических уравнений относительно л+ 4 неизвестных г/1+, ... , г/)+ С с почти ленточной матрицей. Решив эту систему, мы получим значения решения г/+ для g = /+1 = I/ + k. Для нахождения а воспользуемся методом Эйлера, т. е. формулой

aj+i=aj + kC, (6.2.20)

которая следует из уравнения (6.2.17).

Продемонстрируем применение метода дифференцирования по граничному условию на примере задачи 16. По аналогии с уравнением (6.2.11) найдем производную уравнения (6.1.21) по 1 = у{0), рассматривая его как уравнение относительно у{г,1), 6(1) (б = ф2, при сравнении с общими формулами (6.2.1) и (6.2.15) 2 = г и а = б):

При бо = О решение задачи (6.2.1) и (6.2.2) (здесь - уравнения (6.1.21) при условиях г/(0) = 0, г/(1)=1) имеет вид у{г)= 1 и, следовательно, можно положить

1о=1: г/(г, 1)1, б(1) = 0. (6.2.23>

В табл. 6.7 показано влияние шагов h и k на точность получаемых результатов. Ясно, что найденные значения решения даже при сравнительно большом числе шагов по переменной g не слишком точны. Это лишь подтверждает наши выводы, сделанные в п. 5.2.2, о том, что сам по себе метод дифференцирования по параметру (или по граничному условию) не доставляет эффективного алгоритма для продолжения решения по параметру. Эффективный алгоритм, в котором вышеприведенные методы используются в качестве предиктора, а метод Ньютона - в качестве корректора, будет рассмотрен нами в следующем пункте.

Таблица 6.7. Метод дифференцирования по граничному условию для задачи 16 (а = О, у = 20, Р = 0,05). Приведены значения параметра 6 = ф2 при I = 1/(0) = 0,5 (точное значение равно 6 = 1,1546). Видно влияние шагов h w к.

В заключение этого пункта отметим, что метод дифференцирования по граничному условию позволяет проходить точки поворота на диаграмме решений (построенной по параметру а), но не способен, однако, преодолевать точки, где dg/da = 0 (т.е. С = оо). Более подробный анализ метода дифференцирования по граничному условию читатель может найти в работе [6.8].

6.2.3. Алгоритм продолжения типа предиктор - корректор

Как уже отмечалось в предыдущем пункте, зависимости решения от параметра, полученные методом дифференцирования по параметру (или методом дифференцирования по граничному условию) при продвижении вдоль кривой на диаграмме решений могут все более отклоняться от нее. Поэтому здесь, так же как и в § 5.2, мы попробуем построить алгоритм, который будет корректировать такого рода отклонения. В качестве корректора будет использоваться метод Ньютона для соответствую-

Смысл этого равенства нуждается в пояснениях. Однако ниже вы- бор и как длины дуги не используется -Прим. ред.

ЩИМ образом сформулированной задачи, а функцию предиктора возьмут на себя описанные выше методы. Это и будет первый вариант алгоритма продолжения типа предиктор-корректор , основанный на соответствующих разностных заменах исходной задачи (п.п. 6.2.3.1). Другой вариант этого алгоритма (п.п. 6.2.3.2) основывается на использовании метода стрельбы.

.6.2.3.1. Алгоритм, основанный на разностных методах

В качестве примера рассмотрим вновь задачу (6.2.1) и (6.2.2). Точно так же как и в п. 5.2.2, введем новый параметр и, ;полагая при этом

Q (г, ) = -!-, С{и) = . (6.2.24)

Дифференцируя уравнения (6.2.1) и (6.2.2) по и, получаем

aoQ(0) + 6oS(0) = 0, aiQ(l) + 6iQ(I) = 0. (6.2.26)

Заметим, что и играет здесь роль переменной z из уравнений (5.2.12). Для того чтобы и было длиной дуги в пространстве ВХ где г/еВи R, должно выполняться условие, ана^ логичное соотношению (5.2.13), а именно

Qi2 + c2=l. (6.2.27)

Численная реализация этого равенства при разностной аппроксимации уравнений (6.2.25), (6.2.26) приводит к алгоритму, почти идентичному алгоритму DERPAR, описанному в п. 5.2.3. Размерность решаемых задач, однако, может оказаться значительной (при большом числе узловых точек или в случае, когда вместо одного уравнения (6.2.1) у нас имеется система дифференциальных уравнений). Кроме того, здесь всегда приходится использовать специальные методы решения возникающих разреженных систем линейных алгебраических уравнений со специальной (почти ленточной) структурой.

Ниже будет рассмотрена упрощенная схема данного алгоритма. Используя обозначения (6.2.24), выберем предиктор' ъ форме метода Эйлера

у [г, -f А ) = у (г, и) + A Q (г, и), а ( + Ан) = а (н) + ДнС (н),

(6.2.28)

Речь идет о точке поворота по исходному параметру а. - Прим. ред. Имеется в виду кривая на диаграмме стационарных решений.-Прим.

где й и С вычисляются из задачи (6.2.25), (6.2.26) при у = = y{z,u) иа = а(н).При

С(н) = ±1 (6.2.29>

мы получаем метод, формально аналогичный методу дифференцирования по параметру (п. 6.2.1), причем и играет здесь-роль параметра а (на том участке, где С = -1, роль параметра а выполняет величина -и). Если теперь положить

Q(0, н) = ±1, (6.2.30)

то мы получаем вариант метода дифференцирования по граничному условию, описанного в п. 6.2.2. Параметр и играет здесь роль задаваемого граничного значения = г/(0), или, соответственно, -. Шаг Дн в (6.2.28) можно выбирать в зависимости от того, используем ли мы соотношения (6.2.29) илк (6.2.30).

Очевидно, что выбор типа (6.2.29) будет невыгоден в окрестности точки поворота и невозможен в самой этой точке . И, наоборот, выбор типа (6.2.30) будет непригодным в окрестности экстремума зависимости у{0) от параметра а на диаграмме решений. Из этих соображений вытекает алгоритм выбора между двумя указанными возможностями: если последнее вычисленное значение удовлетворяет условию

Q(0, и)<МС, (6.2.31)

то для следующего шага принимается условие (6.2.29). В противоположном случае выбирается условие (6.2.30). Конечно, в обоих этих случаях мы должны соблюдать ориентацию вдоль кривой 2), т. е. знаки -- или - определяются с учетом предыдущих значений С или Q(0). Постоянную М в условии (6.2.31) можно полагать равной 1, если у{0) на соизмеримы, в противном же случае она выбирается с учетом того, какие относительные изменения у{0) или а ожидаются вдоль ветви соответствующей диаграммы решений.

Таким образом, мы разрешили проблему предиктора. В качестве корректора, как и в § 5.2, можно использовать метод Ньютона, применяя его к системе разностных уравнений (6.2.9), (6.2.10). При этом вновь необходимо различать два случая. В первом из них выполнялось условие (6.2.31), и тогда предиктор выбирался в соответствии с формулой (6.2.29), вО