> Более точно: дифференцированием тождеств, возникающих при подстановке решения x{z,r\), y{z,r\) в уравнения (6.1.1), (6.1.2). - Прим. ред.

ных в § 5.7. (Эти методы предназначались для решения систем дифференциальных уравнений первого порядка. Уравнения (6.1.1), (6.1.2) легко преобразуются в систему четырех уравнений первого порядка: = и, и' = -Lf{x, у)/D, у'= v, v= -Lg(x,y)/Dy. Начальные условия (6.1.4а) и (6.1.24) преобразуются к виду м(0) = и(0) == О, x(0) = tii, j/(0) = ti2. Мы будем, далее придерживаться исходных обозначений).

По окончании интегрирования, т. е. в точке z = 1, мы получаем значения решения, зависящие от выбора условий (6.1.24): х{1,1\), х'{1,1[\), у{1,г\), j/(l,Ti). Для того чтобы найденное решение задачи Коши было одновременно и решением исходной краевой задачи, нам необходимо удовлетворить условиям (6.1.4Ь), т. е.

Л(т1) = л;(1, Т1) = 0, 2(л) = г/(1, Т1) = 0. (6.1.25)

Соотношения (6.1.25) представляют собой два нелинейных уравнения относительно неизвестных и Ц2, которое можно решить, используя любой из методов решения нелинейных уравнений, например, метод Ньютона (см. § 5.1). Для вычисления элементов матрицы Якоби, т. е. производных dFi/df\i, можно воспользоваться соответствующими разностными заменами, вычислив функции Fi и / г в точках (tii,ti2), (tii + Atj, т]2), (Ль Tl2 + Ал)- Каждое такое вычисление требует решения задачи Коши (6.1.1), (6.1.2), (6.1.4а), (6.1.24) при соответствующем задании начальных условий. Погрешности, возникающие в процессе интегрирования, могут при этом перекрываться погрешностями аппроксимации использованных разностных формул, и элементы матрицы Якоби могут вычисляться весьма неточно. Поэтому часто, когда это возможно, используются вариационные дифференциальные уравнения (уравнения в вариациях) относительно переменных

pi = dx/dni, Pyl = dy/dr\i, i = 1, 2. (6.1.26)

Вариационные уравнения получаются посредством дифференцирования исходных уравнений') (6.1.1), (6.1.2) по tii и и перестановки дифференцирования по z и т];:

p:,+T:iwp+i-p.,)-0 =-2.

Начальные условия для варьируемых переменных получаются в результате дифференцирования исходных начальных условий (6.1.4а), (6.1.24) по тц и 112

Р.1 (0) = 1, Р.2 (0) = О, р,1 (0) = О, р,2 (0) = 1,

Если проинтегрировать дифференциальное уравнение (6.1.27) вместе с уравнениями (6.1.1) и (6.1.2) и начальными условиями (6.1.4а), (6.1.24), (6.1.28), что в точке z = 1 мы получим

= Р'хЛ) =РхЛ1), (6.1.29)

ж^ру 4S=2(i).

Тем самым, мы имеем матрицу Якоби для применения метода Ньютона, вычисленную на основе интегрирования вариационных уравнений. Заметим, что в данном случае для одной итерации метода Ньютона нам приходится интегрировать систему 12 дифференциальных уравнений первого порядка. При аппроксимации элементов матрицы Якоби соответствующими разностными формулами нужно трижды интегрировать систему 4-х дифференциальных уравнений первого порядка. При этом объем вычислений для большой группы различных функций f У1 g оказывается приблизительно одинаковым. Иногда, правда, удается существенно сократить затраты машинного времени при переходе к вариационным уравнениям, например, при появлении функций ехр, sin, cos, дифференцирование которых дает те же функции.

В случае ГУ1 дополнительные начальные условия к (6.1.3а) выбираются следующим образом:

х'{0) = ци г/(0) = Л2. (6.1.30)

При этом условия, которым нужно удовлетворить после интегрирования от Z = О до Z = 1, имеют вид (см. (6.1.3b)

Fi{n) = x{\)-x = 0, F2i4) = у il)-у = 0. (6.1.31)

Вариационные уравнения (6.1.27) остаются теми же самыми, а начальные условия для варьируемых переменных заменяются на условия

P.iiO)-PyiiO) = 0, i=l, 2,

р;,(о)=1, р;,(о)=о, р;,(о)==о, p;,(o)=i. --

Для ГУЗ в форме (6.1.5) с ненулевыми коэффициентами (с тем чтобы в точке z = 0 эти условия не совпали в ГУ1 или ГУ2)

дополнительные начальные условия в этой точке можно выбрать в виде (6.1.24) или (6.1.30). В случае выбора условий (6.1.24) из (6.1.5а) следует

х'Щ = (У;со - РхоЛОКо, у' (0) = (Yvo - Рг,оЛ2)/%о- (6-1 -33)

При этом вариационные дифференциальные уравнения остаются теми же, а начальные условия заменяются следующими:

Р..(0)=1, Р.2(0) = 0, р^,КО) = 0, р,2(0)=1. P;i(0) = -M/ .o, р;2(0)==0, р;,(0) = 0, р;2(0)=-р,о)/%о-

(6.1.34)

Конкретный вид функций Fi и производных OFi/dt]/ читатель может легко получить с помощью формул (6.1.5Ь).

Конечно, мы могли выбирать недостающие начальные условия в точке z= 1 взамен точки z = 0 и находить решения соответствующих задач Коши на промежутке от z=l до z = 0. В некоторых задачах выбор направления интегрирования может играть существенную роль, поскольку иногда численное интегрирование в одном из направлений оказывается труднореализуемым (соответствующая задача Коши неустойчива по отношению к начальным условиям). Это имеет место, например, в задачах 14 и 15 при больших значениях критерия Пекле, а также в задаче 16. Если задача Коши неустойчива в обоих направлениях, метод стрельбы применять нельзя и следует использовать, например, разностные методы решения, описанные в подпункте 6.1.1.

Рассмотрим теперь примеры расчетов методом стрельбы, иллюстрирующие процесс построения стационарных решений некоторых задач из гл. 4. В качестве первой из этих задач исследуем задачу 11, т. е. систему типа реакция-диффузия (6.1.1), (6.1.2), функции fag для которой имеют вид (Р11-1). В табл. 6.2 приведены некоторые результаты для ГУ2 при выборе начальных условий типа (6.1.24). Отметим, что второе из представленных в таблице решений однородно по пространству. Первое и третье рещения зависят от z и получаются друг из друга симметрией: хЦг) = х^Н1-г), t/i(2) = y 41 -z). В табл. 6.3 представлены соответствующие результаты для ГУ1, при выборе начальных условий типа (6.1.30). Здесь третье решение пространственно однородно: х{г) = 2; y(z) = 2, 3. В обеих этих ситуациях применялся метод Ньютона, причем матрица Якоби подсчитывалась с помощью соответствующих уравнений в вариациях.

Таблица 6.2. Метод стрельбы для задачи 11 в случае ГУ2 (Л = 2, В = 4,6, Dx =0,0016, Dy = 0,008, L = 0,12).

Таблица 6.3. Метод стрельбы для задачи 11 в случае ГУ1 (Л = 2; В = 4,6; Dx = 0,0016; Dy = 0,008; L = 0,12; л:(0) = х = 2; у(0) = у = 2,3).

Используем теперь метод стрельбы для нахождения стационарных решений задачи 14, т. е. для решения уравнений

1 г/ -г/ + Ва(1-г/)ехр- = 0, (6.1.35а)

1 в - в' + В Da (1 - г/) ехр - р (в - в,) = О, (6.1.35b)

соответствующих уравнениям (Р14-7), (Р14-8). Граничные условия при этом имеют вид (Р14-9), (Р14-10), т. е.

Ремг/(0)-г/(0) = 0, Рбнв (0) - в'(0) = О, (6.1.36а) г/(1) = 0, -в'(1) = 0. (6.1.36Ь)

Выберем два недостающих начальных условия в точке 2=1: г/(1) = Ль в(1) = Л2. (6.1.37)

Тогда после интегрирования уравнений (6.1.35) с начальными условиями (6.1.36Ь) и (6.1.37) на промежутке от 2=1 до 2 = 0 мы имеем

, (П) - РеУ (0) - у' (0) = О, F, (п) = Ренв (0) - в' (0) = 0.

(6.1.38)

Результаты решения уравнений (6.1.38) методом Ньютона с использованием соответствующих вариационных уравнений приведены в табл. 6.4. В ней представлен случай, когда существует пять решений данной задачи. Отметим, что область сходимости метода Ньютона для некоторых решений мала. В частности, так обстоит дело для пятого решения. Сходимость к этому решению даже из близкого к нему начального приближения может быть медленной (см. вторую половину таблицы). Наконец, в табл. 6.5 приведены окончательные решения задачи для нескольких различных значений числа Дамкёлера.

Замечание. Во многих задачах концы интервала равноправны и можно использовать метод стрельбы в любом направлении- как справа налево , так и слева направо . В этой задаче есть выделенное направление: решение задачи Коши от 2 = 0 к 2=1 при больших числах Пекле сильно неустойчиво, и такая реализация метода стрельбы здесь не годится.

В качестве последнего примера использования метода стрельбы рассмотрим задачу 15, в которой наряду с дифференциальными уравнениями появляются и иные соотношения (нелинейные алгебраические уравнения).

Будем искать решение y{z), 0(2) дифференциальных уравнений (Р15-6) и (Р15-7) страничными условиями вида (6.1.36).

Таблица 6.4. Метод стрельбы для задачи 14, Рен = 5, Рем =10, у = 20, В = 15, р = 2, вс = О, Da = 0,07.

Таблица 6.5. Метод стрельбы для задачи 14 (Рен = 5, Рем =10, у = В = 15, р = 2, вс = 0).

Решения для последовательных значений Da

При этом в уравнения входят также неизвестные функции (o{z) и 0(2), которые должны удовлетворять соотношениям (Р15-8) и (Р15-9). Для практических вычислений вместо этих нелинейных (алгебраических) соотношений более удобно использовать формулы (Р15-10) и (Р15-11). При фиксированных значениях параметров /м, н, Da, В, у и заданных значениях функций y{z) и 6(2) уравнение (Р15-11) представляет собой при каждом z нелинейное уравнение относительно неизвестной а(2). Решая уравнение (Р15-11), мы находим значения а(2), после чего подставляя их в формулу (Р15-10), вычисляем значения функции 9(2).

Используем для решения этой задачи метод стрельбы. Два недостающих начальных условия опять выберем в точке 2=1 в форме (6.1.37). Затем проинтегрируем уравнения (Р15-6), (Р15-7) с начальными условиями (6.1.36b) и (6.1.37) на промежутке от 2 = 1 до 2 = 0. На каждом шаге интегрирования нам необходимо вычислять правые части дифференциальных уравнений, в которые наряду с параметрами и значениями функций г/ и 6, входят также значения функций а] и 9. Эти значения определяются из формул (Р15-11) и (Р15-10). После проведенного таким образом интегрирования, когда на каждом шаге решается одно нелинейное уравнение, мы получаем в точке 2 = 0 систему двух уравнений (6.1.38) относительно двух неизвестных т)! и т)2. Эта система может быть решена методом Ньютона с использованием вариационных уравнений для переменных

Pyi = ду/дц р^ = де/дц /=1,2. (6.1.39)

Первое из этих уравнений имеет вид

Из этого примера видно, что наряду с вариационными переменными, определяемыми формулами (6.1.39), у нас возникают еще и другие переменные

дсй да dQ dQ /с 1 л 1 \

-df Ж' -щ-- (б--)

Значения этих переменных на каждом шаге интегрирования вычисляются из соотношений (Р15-8), (Р15-9), определяющих а = а (г/, 6) и 9 = 9 (г/, 6). Запишем их в виде

е,(г/, в, а, е) = 0, / = 1,2. (6.1.42)

Предположим, что функции Gi удовлетворяют условиям теоремы о неявных функциях, и пусть значения а (г/, 6) и 9 (г/, в)

для заданных и в найдены. Тогда производные (6.1.41) можно найти, решая две системы линейных алгебраических уравнений

(6.1.43а)

(6.1.43Ь)

где dGi/dy = -Jf, dG2/dy = 0, dGi/двО, dGz/dS =-Jn, a матрица Г определяется как

r-\dGi dGi -,

да dGj L да

dQ dGi 59 -I

(6.1.44)

Описанный подход несложно реализовать в случае, когда нелинейное уравнение (р15-11) имеет одно и только одно решениеа, которое должно удовлетворять естественному с физической точки зрения требованию у < й < 1 (см. формулу (р15-5)).

Значительные сложности возникают тогда, когда уравнение (р15-11) при определенной комбинации параметров и переменных у и в будет иметь несколько допустимых решений (как правило, три различных решения а). Такая ситуация имеет место, в частности, при больших значениях параметра В. В этом случае метод Ньютона, используемый для решения уравнения (р15-11), может оказаться расходящимся или же будет сходиться к какому-либо другому решению, а не к тому, которое ожидалось. В зависимости от того, какой из корней уравнения (р15-11) выбрать, получаются различные функции y{z) и в(2).

Из физических соображений (в случае трех решений) интерес представляют прежде всего два крайних решения а уравнения (р15-11), а именно значение а, лежащее в окрестности значения у, (л~>у (так называемое нижнее решение), и корень, располагающийся в окрестности 1, а <; 1 (так называемое верхнее решение). При решении дифференциальных уравнений (р15-6), (р15-7) мы поступаем следующим образом: в областях параметров, где существует несколько решений уравнения (р15-11), мы всегда рассматриваем (если это возможно) только нижнее решение а (или соответственно верхнее решение а) и

Обычно связанных с устойчивостью найденных распределений концентраций и температуры. - Прим. ред.

тем самым получаем два различных (основных) решения дифференциальных уравнений. Если же комбинировать на разных подынтервалах 2е[0, 1] верхнее и нижнее решения а, то мы получим разрывные профили а (г), 9(2).

На рис. 6.1а приведены профили 0(2), у (г), а (г), 9(2), найденные для случая, когда при всех z выбиралось нижнее решение а уравнения (Р15-11). На рис. 6.1Ь представлен пример профилей решений (для тех же значений параметров), когда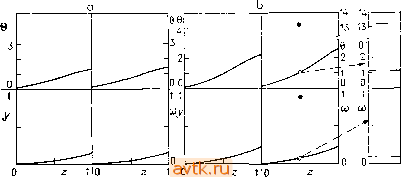

1 0,4Э9 0,5015

Рис. 6.1. Аксиальные профили конверсии и температуры, задача 15; Da = = 0,065, Рвы = 20, Ре = 10, Р = 1, В = 15, у = 20, в. = О, 1м == /я = 25; а) непрерывные профили ш и в, Ь) разрывные профили шив.

а (г) и 9(2) не являются непрерывными функциями (на промежутке 2 е [0,4995; 0,5015] мы рассматривали верхнее решение а). Из сравнения рисунков видно, что профили решений y{z) и 0(z) изменились.

6.1.3. Метод многократной стрельбы

Метод стрельбы, описанный в предыдущем пункте, иногда не позволяет получить удовлетворительные результаты. Так, решение соответствующих задач Коши (включая дифференциальные уравнения в вариациях) может оказаться практически невозможным при наличии сильной чувствительности к начальным условиям. В таких случаях часто оказывается удобным использовать метод многократной стрельбы (см., например, [6.34]).

Опишем кратко идею этого метода на примере задачи (6.1.1), (6.1.2) с граничными условиями ГУ2 вида (6.1.4). По аналогии с п. 6.1.1 выберем на промежутке ze[0, 1] сетку узловых точек 2о = 0, 21, 2 =1, 2,+i > 2,-, которая, вообщс говоря,

может не быть эквидистантной. В практических задачах эта сетка узловых точек выбирается гораздо менее плотной, чем при использовании метода конечных разностей.

На каждом подынтервале [г,-, 2,-+i], t = 0, п-1 уравнения (6.1.1), (6.1.2) интегрируются независимо. Для этого нам необходимо задать начальные условия в точках 2 t = О, ...

п-1; эти начальные значения мы обозначим как tj,-. В точке 2о = О уже заданы два условия (6.1.4а), и поэтому здесь, аналогично тому, как это делалось в п. 6.1.2, мы выбираем два дополнительных условия вида (6.1.24). При этом вектор т)о будет иметь только две составляющих tioi =л;(0) и irio2 = = у(0). Остальные векторы т),-, i=\, п-1 будут иметь по четыре составляющих

Т = (X (2,), Х' (2,), у (2,-), у' (2,)). (6.1.45)

Обозначим решение соответствующей задачи Коши на каждом подынтервале [2г, 2,+i] через x{z) = x{z; г^щ) (и аналогично для x{z), у (г), у'(г)). Метод многократной стрельбы состоит в следующем: так подобрать векторы ti t = 0, ...

n-1, чтобы функции x{z), x{z), y{z), y{z), полученные частями на отдельных подынтервалах [2 Zt+i], оказались непрерывными и чтобы при этом были удовлетворены граничные условия (6.1.4Ь).

Для этого в точках 2(, t = 1, ..., п - 1, должны выполняться условия

{xizr, 2, 1, ii,- i). x(Zi; Zi i, iii i), у(гг, 2, i, TJi-i), ,

w (6.1.46)

a в точке Zn=\ (в соответствии с условиями (6.1.4b)) должны быть выполнены соотношения

(1; n -i) = 0, /(1; 2 ь n -i) = 0. (6.1.47)

Уравнения (6.1.46) и (6.1.47) представляют собой систему из 4(га-1) + 2 нелинейных уравнений относительно 4(га-1)-}-2 неизвестных - составляющих векторов tjo,Чь ....iin-i. Эти уравнения можно решать с помощью любого подходящего метода (например, с помощью метода Ньютона). Для вычисления матрицы Якоби можно опять использовать вариационные дифференциальные уравнения (см. п. 6.1.2). Указанный алгоритм легко модифицируется на случай ГУ1 и ГУЗ; при этом в случае ГУЗ мы выбираем две неизвестных, например х{0), y(0), а затем из уравнений (6.1.5а) находим остальные неизвестные, т. е. л;(0), у'{0). Далее, с помощью условий (6.1.5Ь) мы легко получаем соотношения, аналогичные (6.1.47).