aoso -f aso + а^Чо + ... + iSo + а = Я (Sq), aosi + aisr + a2sr + ... + a -iSi + a = Я (si).

(5.3.10)

боты [5.6, 5.7, 5.8]). Ниже мы рассмотрим только два из них, наиболее простые с вычислительной точки зрения - это метод Крылова и метод интерполяции.

Метод Крылова основывается на тождестве Гамильтона - Кэли

Р(А) = А + а,А -+ ... +а„ ,А + а„1 = 0. (5.3.6)

Умножим тождество (5.3.6) на некоторый вектор h°; в результате мы получим соотношение

aih ~ + flah -f a ih -f аУ = -h , (5.3.7)

где через h* обозначены произведения h* = Ah . Эти векторы могут быть вычислены рекуррентно:

h*+ = Ah*, k = 0, I, n-l. (5.3.8)

Соотношение (5.3.7) представляет собой систему п линейных алгебраических уравнений относительно п неизвестных ai, an. Мы можем ее решить, например, методом исключения Гаусса. Если матрица системы (5.3.7) окажется вырожденной, что представляется маловероятным, то необходимо выбрать другой вектор h°.

Метод интерполяции основан на том факте, что два многочлена степени п, значения которых совпадают в n-f-l различных точках, тождественно равны друг другу. Выберем п -f 1 различных вещественных чисел So, si, s и вычислим значение P{si):

P{Si) = {-l)deti-s). (5.3.9)

Отметим, что в формулу (5.3.9) входит определитель числовой матрицы {S{ - заданное число), и для его вычисления можно использовать программное обеспечение, основанное на методе исключения Гаусса. Построив по точкам (s,-, P{si)), г = О, ..., п, интерполяционный многочлен Лагранжа, мы получим выражение для характеристического многочлена Р{1).

Для построения характеристического многочлена можно воспользоваться также методом неопределенных коэффициентов, записав (5.3.9) в виде системы линейных алгебраических уравнений для коэффициентов ао, а . , ап-

Коэффициент ао должен равняться единице (см. (5.3.5)). Поэтому отклонение ао от единицы можно рассматривать в качестве меры погрешностей (округления), возникаюших в процессе вычислений. (Можно включить равенство ао = 1 в алго-,ритм вычислений и вычислять определитель (5.3.9) только п раз.) Ioi

5.3.3. Критерий Рауса-Гурвица

Для выяснения вопроса о том, все ли корни характеристического многочлена Р(К) имеют отрицательные вешественные части, можно воспользоваться критерием Рауса - Гурвица [5.8]. Обозначим Di = ai и

Z)*=det

(5.3.11)

лля k = 2, 3..... rt (если у > n, то считается, что а, = 0).

Если теперь для всех k выполнены неравенства

D,>0, 2, .... п, (5.3.12)

то все корни многочлена /(?с) имеют отрицательную веше-ственную часть.

Отметим, что определители Di представляют собой многочлены от коэффициентов Р(Я) и, следовательно, являются многочленами относительно элементов матрицы А. При небольших значениях п эти многочлены можно выписать в явном виде.

5.3.4. Нахождение собственных чисел матрицы

Часто оказывается необходимым знать все собственные числа матрицы А, а стало быть, и все (в том числе комплекс-яые) корни характеристического многочлена. Вещественные корни можно найти, например, с помощью метода Ньютона

Р (Я(*)

Р'(Я^)

fe = 0, 1.....

(5.3.13)

задаваясь при этом подходящим образом выбранными началь-гными приближениями Я(°>. Если мы таким способом найдем лее п вещественных корней, то задача решена. Если у нас по-

лучится п-1 вещественных корней, то оставшийся корень также должен быть вещественным. Если найдены п - 2 вещественных корней 1, А,2.....К-2, то можно разделить многочлен Р{Х) на произведение корневых сомножителей вида (X - i) - г) - после чего квадратное уравнение даст нам оставшиеся два корня. Если, наконец, число вещественных корней оказывается меньше, чем п - 2, то после деления на соответствующее произведение корневых сомножителей мы получаем многочлен более высокого порядка, чем 2, решение которого уже нельзя построить в явном виде. Существует целый ряд методов нахождения набора корней вещественного многочлена. Одним из наиболее популярных среди них является метод Лина - Бэрстоу. Здесь мы рассмотрим лишь основную идею этого метода.

Выделим из произведения корневых сомножителей многочлена Р{Х) два множителя, соответствующие либо двум вещественным, либо двум комплексно-сопряженным корням X, и Kk:

Р (X) = (Я2 - {Х^ + Kk)X + KiXk) П (Я - К).

Коэффициенты {%! -f- Хк) и XjXk при таком выборе будут вещественными.

Основная идея метода Лина - Бэрстоу состоит в последовательном нахождении этих квадратичных корневых множителей . Представим многочлен Р{к) в виде

Р (Я) = (Я^ -аХ-) (А, + ЬХ~ + .. . + 6 -2) + АХ + В,

(5.3.14>

где а и р -параметры, которые мы хотим подобрать так, чтобы А = В = 0. Значения аир определяют с помощью итерационной процедуры методом Ньютона.

Самостоятельной проблемой при этом остается выбор начальных значений аир. Предположим, что Р{Х) имеет только простые корни, а именно, 2/е комплексных и т вещественных

корней (2й -{- т - п). Тогда существует + ( ) решений (а, Р)

для уравнений А = О, В = 0. Таким образом, решений может оказаться относительно много, и поэтому вполне вероятно, что метод Ньютона со случайно выбранным начальным приближением аир будет сходиться. Произвольное решение системы Л (а, р)= В(а,Р) = О позволяет понизить степень многочлена на два. Однако при таком последовательном понижении степени многочлена могут накапливаться погрешности (в частности, неточности вычисления аир, погрешности округления

< = ; + б; = /,(х, а) = /,(х-Ьб, а) dfi {i, а)

f,{x,a)+Y,WI = 1. 2, . (5.3.17)

Для стационарного решения х имеем х^ = О, (х, а) = О, и из разложения (5.3.17) мы получаем

б; = а.Д, г = 1, 2, п, а. = -(х, а). (5.3.18)

/-1

Л Т. П.), так ЧТО последние из найденных корней могут оказаться уже недостаточно точными. Эти погрешности можно скорректировать, применяя, например, метод Ньютона или метод Лина - Бэрстоу для исходного многочлена.

Вычисление набора собственных чисел матрицы с помощью характеристического многочлена оказывается эффективным при небольших п. При больших значениях п, например при п > 20 (в зависимости от конкретной задачи), происходит накопление логрешностей округления, и результаты могут оказаться очень неточными, а часто вовсе неприемлемыми. Поэтому для вычисления всех собственных чисел матрицы обычно используются прямые итерационные методы, являющиеся стандартной составной частью программного обеспечения ЭВМ (например, программы EISPACK, MATLAB и др.). В настоящее время чаще всего используется Q?-aлгopитм (см., например, [5.34]). Используя это программное обеспечение, можно эффективно яаходить все собственные числа матрицы с числом строк п, измеряемым десятками.

S.3.5. Нелинейные уравнения - исследование устойчивости в линейном приближении

Обратимся вновь к нелинейной системе (5.1.1)

< = -(1 ) = (5.3.15)

Будем исследовать поведение решения в окрестности ста-дионарного состояния х при заданном а. Введем вектор отклонений решения от х

б = х-х. (5.3.16)

Исходное нелинейное уравнение в окрестности точки х аппроксимируем с помощью формулы Тейлора, сохраняя члены до первого порядка включительно {=d/dt):

(5.3.19)

где £ = ехр (0/(1-f-O/y)). Соответствующий характеристический многочлен имеет вид

р (Х) = 2 - (ац -f- 022) + аца22 - aijOai. (5.3.20)

В соответствии с терминологией, принятой в теории динамических систем на плоскости, будем называть стационарное решение (состояние равновесия) узлом, седлом или фокусом в зависимости от значений собственных чисел 1,

седло: i, 2 вещественные, , 2 < Ol

узел: 1, 2 вещественные, 2 > 0;

фокус: Я 2 комплексно-сопряженные (i = Х2).

Фокус и узел могут быть как устойчивыми, так и неустойчивыми, седло же всегда является неустойчивым. Соответствующие типы решений и значения собственных чисел Xi, Х2 представлены в табл. 5.3.

Из стремления 6{t) к О в (6.3.18) действительно следует, что х(<)->х в силу исходной системы (5.3.15) (при достаточной малости х(0)-х|). Однако доказательство этого совсем не просто; оно было впервые дано А. М. Ляпуновым. - Прим. ред.

Система (5.3.18) представляет собой линейную систему с постоянными коэффициентами, для ее исследования можно воспользоваться результатами предыдущих пунктов. Так, если все собственные числа матрицы А = [ai,] имеют отрицательные вещественные части, то 6->0 при ->оо и, стало быть, принимая во внимание формулу (5.3.16), х->х при -оо). Если некоторые собственные числа матрицы А имеют положительные вещественные части, то стационарное решение х не будет устойчивым. Если, наконец, некоторые из собственных чисел имеют вещественные части, равные нулю, а остальные Re X, < О, то линейное приближение не позволяет решить вопрос об устойчивости стационарного решения.

Результаты, полученные с помощью указанного метода линеаризации, были использованы для выделения областей устойчивости на диаграммах стационарных решений, приведенных в § 5.2. Покажем, как подсчитываются значения Xi и Х2 s табл. 5.2. Дифференцируя по соответствующим переменным правые части дифференциальных уравнений задачи 1, мы получаем (ср. формулу (5.2.17))

--A-Da£, Da{l-x)E/{\+@/yf L-DaB£, -A + DaB(l - x) Е/{1 + @/yf - \

В случае линейной системы (см. п. 5.3 1) выводы были справедливы для траекторий, начинающихся в любой точке пространства Этот термин не является общепринятым.-Прим. ред.

В заключение отметим, что результаты, найденные с помощью метода линеаризации, имеют локальный характер. Это означает, что они говорят лишь о поведении траекторий, которые начинаются вблизи стационарного состояния В нелинейном случае вокруг устойчивого стационарного состояния существует так называемая область притяжения , т. е. область начальных условий, которые дают траекторию, приближающуюся к указанному состоянию. В случае одного устойчивого состояния такой областью притяжения может оказаться все пространство R . Если одновременно существует несколько устойчивых стационарных состояний, то отдельные области притяжения разделяются гиперповерхностями, называемыми сепаратрисами. В случае п = 2 они находятся сравнительно просто (это кривые на плоскости); при п>2 указанная задача становится гораздо более трудной.

5.4. ТОЧКИ ВЕТВЛЕНИЯ СТАЦИОНАРНЫХ РЕШЕНИИ. ВЕЩЕСТВЕННАЯ БИФУРКАЦИЯ

При параметрическом исследовании выбранной задачи нас обычно интересуют все ветви на диаграмме стационарных решений. Как уже отмечалось выше (гл. 3), ветви решений начинаются и заканчиваются в некоторых критических точках. Если мы найдем эти точки, то, естественно, сможем существенно упростить процесс построения диаграммы решений. Критиче- ские точки диаграммы стационарных решений характеризуются тем, что одно из собственных чисел матрицы Якоби для правых частей исходных дифференциальных уравнений равняется нулю. В гл. 3 такого рода точки вещественной бифуркации мы подразделяли на точки поворота и точки ветвления.

В этом параграфе мы займемся анализом алгоритмов нахождения точек вещественной бифуркации, исследуем связь ветвления в окрестности точки бифуркации с процессом продолжения решения, а также рассмотрим способы нахождения точек, в которых возникают изолы - замкнутые кривые, являющиеся компонентами диаграммы решений.

5.4.1. Нахождение точек поворота и точек ветвления

Пусть снова уравнения

fiixu Х2, х„; а) = 0, i=l, 2, .... и, (5.4.0)

Здесь под тривиальным решением мы понимаем решение, которое не зависит от выбранного параметра.

определяют стационарные решения системы дифференциальных уравнений. Для того, чтобы существовали точки (вещественной) бифуркации стационарных решений, необходимо, чтобы (где-то в изучаемой области (х, а)) выполнялось условие

fn+Лхи Х2, Хп, a) = detJ(j;i, Х2, х^, а) = 0, (5.4.1)

где J - матрица Якоби; } = {dfi/dxi]. Равенство (5.4.1) есть отрицание основного условия теоремы о неявных функциях. Оно 4)ормально эквивалентно утверждению о том, что у матрицы J имеется собственное число, равное нулю.

Для того, чтобы в изучаемой области (х, а) существовали точки ветвления, необходимо, чтобы дополнительно к (5.4.1) при некотором k выполнялось условие

fn+2{xu Х2, .... Хп, a) = detJft(j; Х2, х^, а) = О, (5.4.2)

где - матрица, определяемая формулой (5.2.12) и получаемая из матрицы J вычеркиванием k-vo столбца, [dfildfn+i] = - [dfi/да]. В большинстве практических задач для точки поворота (х*, а*) при всех k выполняется условие

/ +2(х', а')¥=0. (5.4.3)

Наоборот, для точки ветвления (х**, а**) из теоремы о неявных функциях следует, что для всех k

/ +2 (х-, а ) = 0. (5.4.4)

Таким образом, соотношения (5.4.3) и (5.4.4) можно использовать для установления различий между точкой поворота и точкой ветвления.

Остановимся теперь на определении так называемых точек первичной бифуркации, т. е. точек бифуркации на тривиальном решении': х(а) = х для всех значений параметра а. При этом уравнения системы (5.4.0) выполняются автоматически, а уравнение (5.4.1) определяет собой соотношение для определения значения параметра а** в точке бифуркации. Решение этого (одного) нелинейного уравнения может быть найдено, например, с помощью метода Ньютона.

В общем случае уравнения (5.4.0) и (5.4.1) образуют вместе систему из п+1 уравнений относительно (п+1) неизвестных координат д;, х1, х\, а' критической точки. Для нахождения решения этой системы мы вновь можем воспользоваться

Рассмотрим простой пример для п=1. Пусть h = xix-a)[ix-lf + a-4]{l-k + k{x-a)) = 0. (5.4.9)

методом Ньютона:

Р'(Х*)ДХ* = -Р(Х*), (5.4.5>

Х*+ = Х* + ДХ\ (5.4.6)

Здесь использованы обозначения X - {xi, Х2, Хп, а), F = = (/ь /г, fn+i), причем F{X) = [dfi/dxj] - 9T0 матрица

Якоби. Последняя строка этой матрицы подсчитывается обычна с помощью соответствующих разностных формул. Формулы для их аналитического вычисления (полезные при небольшом и) представлены в работах [5.9, 5.10].

Рассмотрим теперь точку (х, а), которая удовлетворяет соотношениям (5.1.3), (5.4.1) и (5.4.2), т. е. условиям для точки ветвления. Здесь мы имеем и -f- 2 уравнений для п -f- 1 неизвестных составляющих вектора X. Положим теперь F = (fi. /2...../п+г). Для решения переопределенной системы

F(X)=0 (5.4.7)

воспользуемся методом Гаусса - Ньютона (см. [5.1]):

[F (X*) F (X*)] ДХ* = - F (X*) F (X*). (5.4.8)

Каждое новое приближение мы подсчитываем вновь по формуле (5.4.6). Указанный метод сходится к стационарной точке (минимуму) функции ф = F F; при этом в точке ветвления функция ф имеет минимум, равный нулю (и только в этом случае метод дает нужное нам решение переопределенной системы). Если матрица F(X**) FX**) оказывается невырожденной, то сходимость метода, даваемого формулой (5.4.8), будет квадратической.

Наиболее часто встречающиеся ситуации представлены в табл. 5.5. Конечно, можно найти и соответствующие контрпримеры, однако результаты табл. 5.5, судя по всему, будут верны для большинства практически важных случаев.

Таблица 5.5. Наиболее вероятные ситуации

Диаграмма решений для этого случая изображена на рис. 5.7. Параметр k может принимать два значения k = 0 и k = \ (для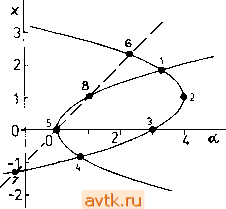

Рис. 5.7. Диаграмма решения примера (5.4.9).

ТВ-точка ветвления, ТП-точка поворота, РТ-регулярная точка.

* При k-0 рассматривать лишь сплошные лннни.

k=l мы имеем двойную точку бифуркации N° 5). Конкретная форма уравнений (5.4.1) и (5.4.2) в данном случае очевидна:

f2 = Qkx + 5{1 -3k - ka) X* + 4 {2ka -k-2)x + + 3 {5ka -3 + 3k)x+2 {-3ka + aik + 2))x + + Д:аЗ-(2Д:+l)a2 + 3(l-Д:)а, (5.4.10)

/з = -kx + 2kx* + 5kx + {k + 2- Qka) x + + i3ka-2{2k + l)a+3il~k))x.

В табл. 5.6 указано число итераций, необходимых для обеспечения неравенства

тах(и*-л:*, а*-а*)<8

(5.4.11)

Таблица 5.6. Исследование примера (5.4.9). Показано число итераций, необходимое для выполнения неравенства (5.4.1).

I) Точки, отпеченные цифрами на рнс. 5.7. ) Стационарная точка ф.

При различных начальных приближениях. Из таблицы видно, что итерационный процесс (5.4.5), (5.4.6) сходится квадратично к точке поворота и линейно (если он вообще сходится) к точке ветвленияИтерационный процесс (5.4.8) сходится квадратично к точке ветвления. Точка № 5 на рис. 5.7 при k = I представляет собой точку ветвления (в ней пересекаются три ветви решения). Характер обоих итерационных процессов можно проследить в нижней части табл. 5.6. Отметим, что процесс (5.4.8) сходится к упомянутой точке лишь линейно.

Для систем больших размеров точное вычисление соответствующих определителей может оказаться довольно трудным делом из-за накопления погрешностей округления. Условие

Итерационный процесс в R и* = ф(и*) сходится линейно (т. е так, как при линейном отображении Ф), если Г/, Сд , О < q < 1. Здесь

Обычно при этом rk - Cq + olq ).

\и' - и

и = lim и Процесс сходится квадратично , если

+1 < С/-. - Прим. ред.