, = sign(). i=l, ...,tt+l. (5.2.15)

Указанные параметры направления будут вычисляться на каждом шаге процесса продолжения. Выбор знака в формуле (5.2.14) определяется, следовательно, соответствующей величиной Nk, взятой с предыдущего шага. Отметим, что оставшиеся производные dxi/dz {1фк) вычисляются по формуле (5.2.13), где коэффициенты f>i известны. Затем после вычисления этих производных мы вновь вычисляем параметры направления Ni и делаем шаг по параметру z. Соответствующая расчетная схема представлена на рис. 5.3, причем для интегрирования дифференциальных уравнений (5.2.13) и (5.2.14) в данном случае используется обычный метод Эйлера.

Проиллюстрируем использование описанного метода продолжения на примере нахождения зависимости стационарного решения задачи 1 от времени задержки т (ср. рис. 5.2). Уравнения (5.1.3) в указанном случае переписываются в виде

и {х, в, т) = -Ах + V (1 - х) ехр -JTWi

tix, в, т) = -Лв +VB(l--)exp-i-aT(e-0,) = O.

(5.2.16)

Начальное условие (5.2.10) при т == О принимает вид 2 = 0: .>: = 0, 6 = 0, т = 0,

Пока Jt невырожденна, р,- конечны н ие обращается в 0.-

Прим. ред.

Таким образом, мы определили производную dxk/dz с точностью до знака. Если индекс k остается неизменным для всего продолжения, то знак в формуле (5.2.14) в процессе продолжения Не меняется ). Отсюда следует, что тогда Xk во время всего процесса продолжения должно либо постоянно возрастать, либо постоянно убывать. Однако это не всегда бывает так, и тогда фиксированный выбор k невозможен. Поэтому в практических ситуациях выбор k осуществляется адаптивным образом-значение индекса k получается в результате применения метода исключения Гаусса (см. выше). При этом знак в формуле (5.2.14) будет определяться тем, возрастает или убывает в этот момент выбранная величина х^ вдоль кривой в направлении возрастания z. Поэтому мы введем знаковые переменные Ni, положив

Задание начального условия Xo.cto при z= О, удовлетворяющего услови/о{,Ь.2.Е).Задание значений параметров направления /Ц,..., . Macujma(fapo-вание неизвестных для метода исключения Гаусса. Задание шага интегрирования z.Oz, х^х, а,о-х„+

Вычисление матрицы системы (5.2.12), т.е. матрицы J={df/dxj}, i. = 1,2,..., n;J=i,2,..., п+1 для значении переменных Ху,...,х„+ = .). Вычисление векто-раf для контроля.Распечотказначенииz,x,...x .,Щ

Решение однородш састемы п ланейныл олгерааческихуравнении {относительно (п+1) неизвестных, с мотрицеи) методом исключения Ш/сса суправляемым SbiifopoM главного элё мента. Результот: индекс к и коэ^лиаиентьг^.,...!,-,, ... р„ (5.2.17}. коэффициент р=1 доопределен.

З^я /=1,2,...,/7+1

sieng)/\/, /=1,2,...,л + -

+Az/ = 1,2,...,/7+1 z +Azz (метод Эйлер и')

Рис. 5.3. Схема метода дифференцирования по длине дуги и метода продолжения Эйлера.

Таблица 5.4. Результаты вычислений по методу продолжения с помощью алгоритма, представленного на рис 5 3 {задача 1 у = 20, В = 10, А= I, 0 = -5, ko=\, а = \) Исходные значения коэффициентов направления: Л^1 = 1, Л^2 = 1, Л^з = 1, масштабные коэффициенты в методе Гаусса Pi = 1, Р2 = 0,1, рз = 1, Дг = 0,01

0,05

.0,02

0,01

0,005

г

в

Ifll

0,5163 4,9664 0,0201 2,9Е - 2

0,5166 4,9676 0,0201 2,2Е - 2

0,5167 4,9682 0,0200 ,ЗЕ - 2

0,5168 4,9685 0,0200 5,6Е - 3

0,5168 4,9686 0,0200 2,9Е - 3

0,5168 4,9686 0,0200 1,5Е-3

2 X 0

0,9665 11,814 -0,1286 8,2Е1

1,1904 11,912 -0,0005 1,0Е1

0,9972 11,869 -0,1128 1,5Е1

0,9997 11,818 -0,1084 1,1Е1

0,9736 6,0281 0,3360 6,2Е - 1

0,9797 6,3726 0,3010 2,1Е0

При выборе главного элемента в строке 1 берется тах(р; а^у Аналогично иа следующих шагах метода исключения.

Применим теперь вычислительный алгоритм, соответствующий расчетной схеме рис. 5.3, для случая различных шагов интегрирования Az. Результаты вычислений представлены в табл. 5.4. Первая часть этой таблицы может быть использована для более глубокого уяснения метода. Читатель может легко сопоставить полученные результаты с данными рис. 5.2 для а = I. Вторая часть таблицы характеризует влияние погрешностей аппроксимации при выбранном методе интегрирования. При этом чем меньше шаг интегрирования, тем лучше найденные значения аппроксимируют реальную зависимость. Из таблицы видно, что даже в случае рассматриваемой простой задачи для получения достаточно точных результатов нам пришлось бы выбирать Az очень малым. Это обусловлено, конечно, в первую очередь низким порядком аппроксимации используемого метода Эйлера (погрешность аппроксимации в этом случае есть 0(Az)). Если выбрать более эффективный метод интегрирования, например метод Рунге-Кутты 4-го порядка, то результаты окажутся более точными. Полученное решение, однако, также, хотя и в меньшей степени, будет отличаться от истинной зависимости. Вследствие этого представляется необходимым после прохождения некоторого интервала изменения переменной Z всегда уточнять решение, т. е. корректировать его так, чтобы выполнялось исходное уравнение (5.1.3), или, для рассматриваемого случая, уравнения (5.2.16). Так появились методы продолжения типа предиктор-корректор, которые мы опишем в следующем пункте.

5.2.3. Алгоритм продолжения типа предиктор-корректор

В принципе существуют две возможности коррекции погрешностей аппроксимации, накапливающихся при продолжении решения с использованием простого предиктора. Первая из них заключается в том, чтобы контролировать, как отличается решение от истинного, например, по норме f, и когда это отличие превышает некоторый заранее заданный допуск, использовать для уточнения результатов какой-либо итерацион-

а (расширенная) матрица Якоби J системы (5.2.16) (если обозначить Е = ехр (в/ (I + e/v))) записывается как

-A~koxE, M£z, ko(l-x)E

I -k,TBE, -A + °(f~] - ат, koB (I -x) £-а(в-в,)J

(5.2.17)

НЫЙ метод (например, метод Ньютона). При другом подходе также используется метод Ньютона, но после каждого шага предиктора. При этом в методе Ньютона осуществляется лишь такое число итераций, чтобы приращение Ах по соответствующей норме оказалось бы меньше заданной точности вычислений. В обоих подходах уточняются выбранные /г из п -f 1 переменных Хи Хп, Хп+1 = а.

Выбор неизменяемой переменной (ее индекса k) не является произвольным: например, в окрестности предельной точки это не может быть а, а в окрестности экстремума xt это не может быть Xi. Поэтому алгоритм выбирает ее сам, причем одной из возможностей является использование того же самого механизма, что в п. 5.2.2. Диаграмма вычислений для описанного алгоритма продолжения типа предиктор-корректор представлена на рис. 5.4. В работе [5.5] этот алгоритм расписан на языке Фортран, соответствующая подпрограмма называется DERPAR. В данной книге мы будем использовать это название. Отметим, что в этой подпрограмме вместо метода Эйлера в предикторе используются варианты многошагового метода Адамса-Башфорта переменного порядка.

Приведенный алгоритм продолжения беспрепятственно преодолевает точки поворота на зависимостях решения от параметра. В точках же ветвления он обычно дает продолжение первоначальной ветви решения. Продолжение может не удаться, если очередная вычисленная точка окажется слишком близкой к точке ветвления. Сигналом, указывающим, что мы перешли за точку ветвления, может служить изменение знака detJfe определителя матрицы J*. Таким образом, указанный алгоритм формирует зависимость решения от параметра, представляющую собой непрерывную кривую в (п + 1)-мерном пространстве переменных Хи Хп, Хл-н = а. Разумеется, алгоритм DERPAR не приспособлен для того, чтобы с его помощью построить всю диаграмму решений целиком. Для каждой изолированной ветви кривой f{x,a) = 0 ему нужна новая начальная точка, которую можно получить, например, методом случайного перебора начальных приближений для схемы Ньютона (см. § 5.1). Наконец, отметим, что описанный алгоритм не рассчитан на точное нахождение бифуркационных точек в пространстве (х, а). Обнаружив такую точку, ее координаты можно точно вычислить с помощью алгоритмов, описанных в п. 5.4.1, и определить затем соответствующие начальные значения для процесса продолжения на остальных ветвях решения (см. п. 5.4.2).

В последнее время был разработан целый ряд методов и алгоритмов, связанных с процессом продолжения (см., например,

работы [5.24], [5.25]), где большей частью используется практически тот же подход, что и в алгоритме DERPAR.

(нЛЧАП0\

Задание начальных значений переменных л-, ..., л- +, и парамвтрод Pi, Nj, i-1,. . ., п+1

т-► Вычисление fui при х., а- .,

Решение неоднородной системы п линейных уравнений с матрии,ей для нахождения ньютонода приращения Ах одновременно с решением однородной системы с матрии,ей J {.см. рис. 5.3) для нахождения индекса к и значений [3,-, ..., +!, 1,ь.х^=

Вычисление х^,...,х„., (en(S.i .4))

1дх<6 у

Распечатка х^,...,х ЛП

Коней, процесса продолжения. Кривая замкнулась или значения -v ..., х„ перешли заданные границы

Вычистние N, i=1,...,n+1

аналогично рис. 5.3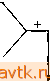

Один шаг интегрирования методам Адам-са-Бзшфарта (порядок метаво

Рис. 5.4. Схема алгоритма продолжения DERPAR.

Результат применения алгоритма продолжения DERPAR для задачи 2 [5.5] представлен на рис. 5.5. При этом вся кривая целиком была построена путем одного обрашения к алгоритму. Отметим, что на диаграмме решений имеется 6 точек поворота и отсутствуют точки ветвления. Точка пересечения трех ветвей на рисунке не является точкой бифуркации, по-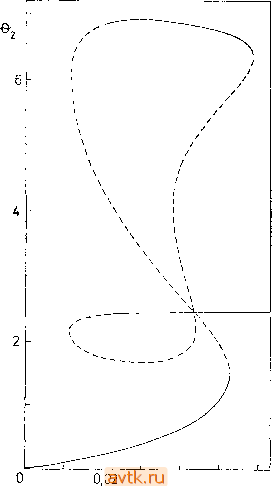

0,04 о( 0,06

Рис. 5.5. Диаграмма стационарных решений задачи 2, у = 1000, В = 22, Pj = Р = 2, 0 = в^ = 0: Л = 1, a=Daj = Da сплошные линии - устойчивые решения, штриховые - неустойчивые решения.

1 3 510 30 г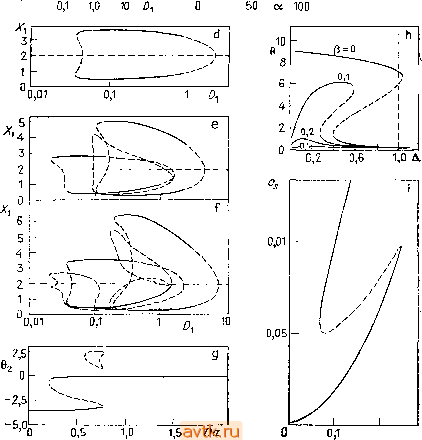

Рис. 5.6. Диаграммы стационарных решений некоторых задач из главы 4; сплошные линии - устойчивые решения, штриховые линии - неустойчивые решения, а) Задача 8, каскад из двух реакторов с однонаправленным течением, уравнения (Р8-2а), (Р8-За), (Р8-4), (Р8-5); /4 = 2, 5 = 4, = = lODi. b) Задача 4; у = 3, р = 1,5; Vo = 0,01. с) Задача 10; о = 16. 6 = 4. d) ЗаЗача 8; = 2, уравнения (Р8-2)-(Р8-5); /4 = 2, 5 = 6, = = lODi. в) Задача 8; iV = 3, уравнения (Р8-7)-(Р8-12); /4 = 2, 5=6. Д2= 10Д,. f) Задача 8; N = 4, уравнения (Р8-7)-(Р8-10), (Р8-14) -(Р8-17), /4 = 2, 5 = 6, 1)2= ЮД,. Зайача 2; у = 20, Л=1, 0, = 0 = - 5. = = Ь S = 15> Da = Daj = Da- ) 5айача 1; у = 20; 5 = 9, 0с=О. Da = 0,02. i) Задача 5; значения параметров см. в табл. 4.1.

= Ах (5.3.1)

имеет (в случае невырожденной матрицы А) единственное стационарное решение х = 0. Если у матрицы А нет кратных

*> Во многих задачах нахождение стационарных решений есть лишь первый шаг, основной же интерес представляют периодические (или еще более сложные) решения. - Прим. ред.

скольку значения трех других переменных состояния на каждой из ветвей оказываются разными.

Построение диаграммы решений представляет собой важнейшую задачу анализа нелинейной динамической системы Читателю, который хочет практически освоить эту проблематику, мы советуем рассчитать несколько диаграмм решений самостоятельно. На рис. 5.6 изображены 9 диаграмм решений для различных задач, рассмотренных в гл. 4. Диаграммы решений, представленные на рис. 5.6b, h,i, можно получить с помощью отображения соответствующего параметра. Диаграмму на рис. 5.6с можно построить аналитически. Начальные значения для продолжения решений на рис. 5.6d, е, f читатель найдет в табл. 5.1 при Di = 0,4.

5.3, ИССЛЕДОВАНИЕ УСТОЙЧИВОСТИ СТАЦИОНАРНЫХ РЕШЕНИЙ

В этом параграфе, который носит вспомогательный характер, мы опишем методику исследования устойчивости стационарных решений по линейному приближению. Как известно, устойчивость решения зависит от собственных чисел матрицы линеаризованной системы. Мы коротко рассмотрим методы нахождения коэффициентов характеристического многочлена матрицы и приведем критерий устойчивости Рауса - Гурвица. В дальнейшем мы используем характеристический многочлен при на.хож-дении бифуркационных точек (§§ 5.4, 5.5, 5.8), а также для определения устойчивости периодических решений (§ 5.8). Наконец, мы напомним о методе нахождения собственных чисел матрицы непосредственно как корней характеристического многочлена, что является более предпочтительным при небольших размерах системы.

5.3.1. Линейные уравнения

Система линейных дифференциальных уравнений с постоянными коэффициентами

собственных значений, то решение системы (5.3.1) можно представить в виде

x(0=ZQ[...],eV (5.3.2)

где в квадратных скобках стоит либо собственный вектор матрицы А, соответствующий вещественному собственному числу %i, либо ограниченная векторная функция переменной t, если h - мнимое число. Постоянные С, определяются начальным условием х(0). Из разложения (5.3.2) следует, что устойчивость (в данном случае глобальная) стационарного решения системы (5.3.1) определяется вещественными частями собственных чисел Xi. Если для любого собственного числа матрицы А имеет место условие

Reh<0, г=1, га, (5.3.3)

то нулевое стационарное решение является асимптотически устойчивым; в частности, для всякого решения системы (5.3.1) выполняется условие

lim 11x (011 = 0. (5.3.4)

<->оо

Если какое-нибудь собственное число имеет положительную вещественную часть, то нулевое решение, очевидно, неустойчиво: существуют решения х(), для которых x(i) оо при оо (и сколь угодно малых х(0)). Эти утверждения справедливы и для случая кратных собственных чисел. При этом в квадратных скобках в разложении (5.3.2) появляются многочлены от t, однако, как известно, экспоненциальная функция убывает (или возрастает) быстрее, чем многочлен любого порядка.

5.3.2. Характеристический многочлен

Собственные числа матрицы А являются корнями характеристического многочлена

Р (Я) = (-1) det (А - Я1) = Я + аХ~ +

...+а„ ,А + а„. (5.3.5)

Для п = 2 или 3 мы можем получить характеристический многочлен прямо из определения детерминанта. Для больших же значений п этот процесс оказывается очень трудоемким и неудобным даже при использовании ЭВМ.

Существует целый ряд методов для вычисления коэффи-диентов характеристического многочлена (см., например, ра-