в этом случае для определения коэффициента избирательности аи и полосы пропускания 2Аипи по напряжению можно воспользоваться формулами (11.59) и (11.60) для случая /?г>2э, в которых добротность Q следует заменить добротностью Q, учитывающей щунтирующее действие сопротивления Rr. Действительно, при ре-зонансе эквивалентное сопротивление контура с учетом Rr равно параллельному соединению Zap и Rr, т. е.

ZpRp

Zap-

Zap -t-

1 +Z3p ?p

(11.61)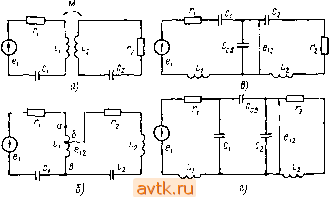

Рис. 11 и

Тогда в соответствии с формулой (11.50)

р р

1 +2эр ?;

ИЛИ

Q

1 4- Z,p/R

(11.62)

§ 11.4. Вынужденные колебания в связанных контурах

Два контура называются связанными, если между ними существует электрическая связь, благодаря которой часть энергии из первого контура может передаваться во второй н наоборот (рис. 11.11). Контур, отдающий энергию, называется первичным, а потребляющий ее от связанного с ним первичного контура - вторичным. Различают следующие виды связи: трансформаторную, автотрансфорйатурную (рис. 11.11, б) и емкостную (рис. 11.11, в, г).

При трансформаторной связи (рис. 11.11, а) протекающий в первичном контуре переменный ток /] создает в катушке индуктивности Li магнитный поток, который наводит ЭДС взаимоиндукции в катушке индуктивности Lz вторичного контура.

ЭДС взаимоиндукции

En=-HxM==-XJ (11.63)

где М - коэффициент взаимоиндукции; XcejaiM - сопротивление связи.

Рнс. 11.12

Под действием ЭДС JS12 во вторичном контуре протекает ток /2, который наводит в катушке L, первичного контура ЭДС взаимоиндукции

E =-XJ2. (11.64)

Предположим, что каждый из контуров настроен в резонанс на частоту шр источника ЭДС ei = £i sin щ1 (такой резонанс называется полным). Тогда сопротивления контуров имеют активный характер и ток /ip, протекающий в первичном контуре, совпадает по фазе с напряжением Ei. ЭДС взаимоиндукции отстает по фазе от тока /jp на 90°. Ток /2 совпадает по фазе с ЭДС Еу2 и равен

IpEiJr/ioM/r. (11.65)

ЭДС £21 отстает по фазе от тока /2 на 90° и равна

£-21 = /2р )рЖ = Лр. (11.66)

Векторная диаграмма токов и напряжений связанных контуров ДЛЯ рассмотренного случая приведена на рис. 11.12, а. Из временной Диаграммы рис. 11.12, а видно, что ЭДС £21 направлена в сторону, противоположную направлению ЭДС Ей Следовательно, Ток Д в первичном контуре при резонансе будет определяться выражением

1,р={Е,-Еп)1г^.

(11.67) 215

с учетом (11.66) выражение (11.67) можно записать как

/хрА/К + С^рЛ))/. (11.68)

Подставляя (11.68) в выражение (11.65), будем иметь

/.р =--= . (11.69)

Из выражения (11.68) можно сделать вывод, что при резонансе обоих контуров влияние ЭДС £21 на ток /1 можно рассматривать как внесение в цепь первичного контура активного сопротивления

Г„ = (* рМ)2/г2.

Таким образом, систему связанных контуров, настроенных в полный резонанс, можно Рис. 11.13 представить как эквивалентный контур, изоб-

раженный на рис. 11.13. Тогда мощность, выделяемая во вторичном контуре, определяется из выражения

Я2=/1оГ1=£кн/(Г:+г„.) (11.70)

Записав выражение для мощности, расходуемой в первичном контуре:

найдем КПД системы связанных контуров;

= Р2/(Л + 2) = Гз /(Гз + Г1)=1/(1+Г1/Гв ). (11.71)

Настройка контуров в полный резонанс производится в такой последовательности. Сначала при разомкнутом вторичном контуре (связь отсутствует) настраивают в резонанс первичный коп-тур, создавая Ji = 0. Очевидно, условием резонанса несвязанного первичного контура является Х^О. Затем осуществляют связь между контурами и настраивают вторичный контур. Так как прн Xi=0 реактивное сопротивление не вносится во вторичный контур, то условием резонанса вторичного контура будет 2 = 0. При Xi=X2 = 0 поступает полный резонанс в связанных контурах.

Если вторичный контур не настроен в резонанс с частотой источника ей то вид векторных диаграмм зависит от характера сопротивления вторичного контура.

На рис. 11.12, б приведена векторная Диаграмма в случае индуктивного сопротивления вторичного контура. На векторной диаграмме ток /2 отстает по фазе от ЭДС £12 на некоторый угол ф. Вектор £21 можно разложить на две составляющие - активную £2u и реактивную Ezip, а влияние £21 на h рассматривать как внесение в цепь первичного контура комплексного сопротивлении

isH. имеющего активную Гвн и реактивную Хвн составляющие. Найдем значение сопротивления

Записав h = EnlZ2, где Z2 = r2+/.X2 - сопротивление вторичного контура, Г2, Хг - активная и реактивная составляющая Z2, с учетом (11.63), будем иметь

л ~~ ifl I2Z2 ~ Z2 ~Г2 + ]Х2

Умножив числитель и знаменатель выражения на сопряженное комплексное число Гг-Дг, получим выражение

/ 2 + Л2 2 + 2

в котором первый член представляет собой активную составляющую вносимого сопротивления

а второй - реактивную составляющую

в„=-. (11.74)

2 + -2

Из выражения (11.72) следует, что прн индуктивном сопротивлении вторичного контура вносимое им сопротивление Zbh в цепь первичного контура имеет емкостный характер.

Внесение сопротивления Zbh в первичный контур нарушает условие резонанса Ji = 0 в нем на частоте ир. Теперь резонанс, называемый частным, наступает при условии

:~-вн=0,

или

: = -ви, (11.75)

где Х\ - реактивное сопротивление первичного контура.

Заменяя Хвн в (11.75) его выражением из (11.74), будем иметь'

:=-42. (11.76)

Полагая, что контуры имеют одинаковые параметры Li = L2 = =L, Ci = C2 = C, Г1 = Г2 = г, можно записать

Xi=X2=X=mL-lj(wC). (11.77)

Тогда условие частного резонанса (11.76) будет иметь вид

(11.78)

/ 2+2

Полагая теперь, что при расстройке контура выполняется неравенство г<Х. выражение (11.78) можно записать как

или

>Х-1/( )С)=± >Ж. (11.79)

Разделив левую и правую части выражения (11.79) на coL и учитывая, что 1/{ЬС)~а)о\ получим уравнение

ш1/ш^=\±М/1. (11.80)

Решая уравнение (11.80) относительно ш, найдем две резонансные частоты первичного контура, обусловленные внесением в цепь контура сопротивления:

. >р1= о тте в; (11.81)

>р2= о Ь=Ж в. (11-82)

где /CcB=M/L - коэффициент связи, характеризующий степень взаимного влияния двух контуров.

Из формул (11.81) и (11.82) следует, что резонансная частота йр1 лежит ниже, а частота Wp2 - выше собственной частоты контура ао.

Определим характер резонансных кривых системы двух связанных одинаковых контуров. На резонансной частоте ар=соо этих контуров будем иметь Xi=X-i=X = 0. Тогда ток /ар можно определить из выражения (11.69). При увеличении коэффициента связи, например за счет увеличения М, ток /ар сначала возрастает, достигая максимального значения /арmax, а затем уменьшается. Значение коэффициента связи /Ссвкр при /артах называется критическим.

Математически можно доказать, что максимум тока hp в формуле (11.69) получается при условии

г,=Гз . (11.83)

При этом же условии достигается и максимальное значение выделяемой во вторичном контуре мощности. Из формулы (11.70) имеем

Максимальный коэффициент полезного действия найдем из формулы (11.71) с учетом равенства (11.83):

шах=1/2.

На частоте ио, отличной от резонансной, при значениях коэффициента связи, меньших критического значения С/Ссв</Ссв кр). вносимое реактивное сопротивление Хвн мало и не может скомпенсировать собственное реактивное сопротивление контура X. Поэтому резонансные кривые в данном случае соответствуют кривым 1 и 2 (рис. 11.14) и имеют такой же вид, как и для одиночного контура. Резонансная кривая при Ксв = Ксв.кр соответствует кривой 3.

0,707 -i-*t-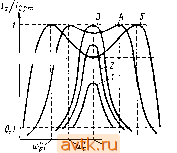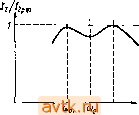

iOpl О)

Рис. 11.14

Рис. 11.15

При КсвЖсв.кр резонансные кривые связанных контуров соответствуют двугорбым кривым 4. 5 на рис. 11.14, у которых ток hp на частоте шо меньше своего максимального значения /гртСсоо), а на частотах copi и ирг равен значению /гртСюо). Действительно, на частоте т при /Ссв>/Ссвкр условие (11.83) не выполняется, поэтому /2рСсОо)</2рт(сОо).

На частотах частного резонанса copi и Шр2 активная составляюшая вносимого сопротивления согласно выражению (11.73) с учетом условия (11.78) равна собственному активному сопротивлению, т. е.

Гв = Г2. (11.84)

Так как Г1 = Г2 = г, то можно записать ApCropi) =/2рСсор2) =/2ртСа)о).

При Г1ФГ2 двугорбые резонансные кривые становятся несимметричными (рис. 11.15).

При емкостном характере собственного сопротивления Z2= = Г2-JX2 вторичного контура ток контура h опережает вектор ЭДС Ei2- Векторная диаграмма для этого случая приведена на рис. 11.12, в, из которой видно, что вносимое в первичный контур сопротивление Zbh имеет индуктивный характер.

Условие частного резонанса (11.76), выведенного для случая индуктивного сопротивления вторичного контура, сохраняется и При емкостном характере сопротивления контура.

В пределах /Сев кр</Сев<2,41 /Ссвкр форма резонансных кривых Контуров с трансформаторной связью приближается к прямо-

угольной, что позволяет получить высокую избирательность устройства связи при заданной полосе пропускания. Таким образом, связанные контуры можно использовать в качестве полосовых фильтров. Прямоугольность резонансной кривой оценивают с помощью коэффициента прямоугольности, равного отношению полосы пропускания к ширине резонансной кривой на уровне 0,1, т. е.

Л: р = 2Дш /(2Ди)о,1). (11.85)

Кроме трансформаторной применяется автотрансформаторная и емкостная связь.

При автотрансформаторной связи (см. рис. 11.11, б) взаимодействие между контурами осуществляется с помощью общей ка- тушки индуктивности Li. Напряжение ei2,

г---K-iiA питающее вторичный контур, прямо пропор-

j ционально числу витков аов между точками

Q б К в катушки. Следовательно, с увеличением (Обе связь между контурами возрас-тает.

При емкостной связи между контурами

Т напряжение ei2, питающее вторичный кон-

р^ Л jg тур, зависит от емкости конденсатора связи.

Емкостную связь можно разделить на внутреннюю и внешнюю. При внутренней (см. рис. 11.11, в) с уменьшением Сев связь между контурами возрастает, так как в этом случае увеличивается сопротивление связи Л^св= 1/(шСсв) и, как следствие, напряжение ei2.

При внешней связи (см. рис. 11.11, г), наоборот, связь возрастает с увеличением емкости конденсатора Сев.

При разработке монтажных радиотехнических схем следует учитывать, что между близко расположенными катушками индуктивности может возникнуть паразитная связь, которая бывает индуктивной (трансформаторной) и емкостной. Для устранения индуктивной связи катушку экранируют от соседней металлическим экраном. Магнитное поле экранированной катушки не проникает за пределы экрана, так как этому препятствуют вихревые токн, создаваемые полем катушки. Однако близко расположенный экран может существенно изменить параметры катушки, в частности уменьшить добротность. Поэтому экран располагают на расстоянии не меньше 5 мм от катушки.

Для устранения емкостной паразитной связи используют металлические экраны, заземленные на корпус схемы. При этом емкость связи Ссв.пар заменяется двумя последовательно соединенными емкостями, общий вывод которых заземлен (рис. 11.16).

Вопросы и задачи для самопроверки

1. Из каких элементов состоит колебательный контур?

2. Определить значение энергии, запасаемой в электрическом поле, образованном между пластинами конденсатора, емкостью 1 мкФ, если переключатель П находится в положении 1 (рис. 11.1, б). Напряжение батареи Е составляет 10 В. Ответ. Wc = bQ мкДж.

3. Как изменяется энергия электрического поля конденсатора в схеме рис. 11.1, б при переключении переключателя П нз положения 1 в положение 2?

4. Какова максимальная энергия магнитного поля катушки колебательного контура с индуктивностью L=\ Гн (рис. 11.1, а), если максимальный ток контура равен 0,1 Л? Потерями энергии в контуре можно пренебречь, т. е. г = 0. Ответ. 7=0,005 Дж.

5. Определить максимальный ток, протекающий через колебательный контур, состоящий нз индуктивной катушки L = \ Гн и конденсатора С=100 мкФ. Л1ак-снмальное напряжение на конденсаторе L/cirax=100 В. Потерями энергии в контуре можно пренебречь (/ =0). Ответ. /тах=1 А.

6. Определить волновое сопротивление контура, элементы которого имеют следующие номиналы: Z. = 10 Гн; С=10 мкФ. Ответ. р = 1000 Ом.

7. Что такое добротность Q колебательного контура? Как она зависит от величины потерь энергии, возникающих за счет активного сопротивления контура?

8. Определить добротность контура, состоящего из катушки индуктивности L-\ Гц и конденсатора С=1 мкФ. Активное сопротивление контура /-=10 Ом. Ответ. Q = 100.

9. Определить реактивное сопротивление последовательного колебательного контура (рис. 11.5, о) с элементами L=\ Гн, С=1 Ф, если на контур воздействует источник переменного напряжения с частотой /=10 Гц. Будет ли эта частота резонансной? Ответ. Jr=JrL-Гс= (6,28-10-16) Ом=6 246 Ом. Следовательно, полное реактивное сопротивление контура носит индуктивный характер.

10. Определить полное сопротивление колебательного контура (рнс. 115, а), если активное и реактивное сопротивления соответственно равны /- = 10 Ом, Х= = 30 Ом. Ответ. г = 32 Ом.

11. Чему равно полное сопротивление последовательного колебательного контура (рнс. 11.5, а) прн резонансе? Почему?

12. Определить резонансную частоту последовательного колебательного контура с элементами L=\ мГн, С=10 мкФ. Ответ. /р=1,6 кГц.

13. Во сколько раз напряжения на индуктивной катушке и конденсаторе последовательного колебательного контура превышают прн резонансе ЭДС источника?

14. Начертить векторную диаграмму последовательного колебательного контура для случая резонанса.

15. Где используется резонанс напряжений, возникающий в последовательном контуре?

16. Что такое резонансная кривая последовательного контура? Как по виду Этой кривой определить добротность контура?

17. Определить резонансную частогу последовательного контура, если добротность и полоса пропускания контура равны 200 и 500 Гц. Ответ. /р=100 кГц.

18. Определить добротность, резонансную частоту и полосу пропускания последовательного контура с параметрами L=0,01 Гн, С=100 пФ, /-=100 Ом. Ответ. /р=160 кГц, Q=100, Лш =1,6 кГц.

19. Начертить векторные диаграммы токов в параллельном колебательном Контуре (рис. 11.5, б) для трех случаев: а) й)>Шр; б)ш = (Вр; в) ш<Шр.

20. Почему резонанс в параллельном контуре называют резонансом токов? Во Сколько раз ток в каждой из ветвей параллельного контура превышает ток в общей цепи?

21. Определить резонансную частоту параллельного колебательного конту-I а с параметрами L=0,1 Гн. С=1000 пФ. Совпадает лн выражение для резо-

нансной частоты в параллельном контуре с выражением для резонансной частоты в последовательном? Ответ. /р=16 кГц.

22. Какой характер (индуктивный, активный или емкостный) носит эквивалентное сопротивление Zjk в параллельном колебательном контуре при резонансе?

23. Нарисовать резонансные кривые параллельного контура для трех случаев: а) Z,K i?r; б) 7эк</?г; в) Z, соизмеримо с Rr.

24. Найти по резонансным кривым параллельного контура для случая 2эк=з 7?г полосу пропускания по току и напряжению.

25. Определить, во сколько раз уменьшится добротность параллельного контура с учетом шунтирующего действия сопротивления генератора колебаний /?г = =400 Ом. Эквивалентное сопротивление контура при резонансе 2эр=200 Ом. Ответ. В 1,5 раза.

26. Найти полосу пропускания по напряжению параллельного контура, если добротность с учетом шунтирующего действия внутреннего сопротивления генератора и резонансная частота контура равны 60 и 120 кГц. Ответ. 2Au>nu = 2 кГц.

27. Какие виды связи существуют между контурами?

28. Определить коэффициент трансформаторной связи контуров (рис. 11.11, а), имеющих индуктивность катушек связи L = L2=0,1 Гн. Взаимная индуктивность M=0,01 Гн. Объяснить физический смысл коэффициента связи. Ответ. Ксв=ОЛ.

29. Начертить и объяснить векторную диаграмму связанных контуров.

30. Какое сопротивление (индуктивное, емкостное или активное) вносится в первичный контур вторичным контуром (рис. 11 И, а), настроенным в резонанс с частотой источника?

31. Определить величину сопротивления, вносимого вторичным контуром (рнс. 1111, а), настроенным на резонансную частоту источника юо=100 кГц, в первичный контур при трансфор.маторной связи между контурами Взаимная индуктивность jW=0,001 Гн. Активное сопротивление вторичного контура Г2= = 100 Ом. Ответ. Гв =Ш Ом.

32. Начертить резонансные кривые контура (рис. 11 11, а) при различной степени связи. Собственные резонансные частоты контуров равны между собой.

33. Определить сопротивление, вносимое в первичный контур вторичным контуром (рис. 11 11, а), при критической связи между ними. Активное сопротивле-не первичного контура ri=\5 Ом.

34. Определить полосу пропускания связанных контуров (рис. 11.11, а) с добротностью Q=141 при критической связи между ними. Собственные частоты контуров /о1=/о2=/о=100 Гц. Ответ. Я=2Д(Вс; = 1000 Гц=1 кГц.

35. Определить характер резонансной кривой при Гвн>Г1 для контуров, имеющих равные собственные частоты и связанных трансформаторной связью.

ГЛАВА 12

ГЕНЕРАТОРЫ СИНУСОИДАЛЬНЫХ КОЛЕБАНИИ

§ 12.1. Принципы построения генераторов

Схемы, с помощью которых энергия источника питания преобразуется в энергию переменных электрических колебаний при отсутствии внещнего сигнала, называются генераторами.

Колебания на выходе генератора можно получить, охватив обычный усилитель положительной обратной связью (рис. 12.1)-При выполнении условий (см. § 2.2)

АГ В=1; (12.1)

, ?, + % = 0 < . (12.2)

Б усилителе с положительной обратной связью возникают незатухающие колебания, так как первоначальное изменение напряжения на выходе схемы, возникшее за счет случайных колебаний (флуктуации) на входе усилителя, передается по цепи обратной связи снова на вход, усиливается и вызывает еще большее изменение выходного сигнала.

С нарастанием амплитуды выходных колебаний рабочая точка каскадов, составляющих усилитель, заходит в нелинейную область динамических характеристик трап-

зисторов усилителя и коэффициент уси-

ления Ки уменьшается до значения, при котором /СиР=1; устанавливается стационарная амплитуда колебаний на выходе схемы.

Равенство (12.1) показывает, что усилитель усиливает сигнал во столько раз, во сколько ослабляет его цепь обратной связи, и называется условием б а- Рис.12 1

ланса амплитуд.

При балансе амплитуд энергия источника питания через цепь положительной обратной связи компенсирует потери энергии в схеме.

Равенство (12.2) называют условием баланса фаз.

В зависимости от вида фазочастотных характеристик усилителя и цепи обратной связи условия баланса амплитуд и фаз могут выполняться для целого спектра частот и для одной частоты. В первом случае на выходе генератора будем иметь колебания сложной формы, во втором схема генерируег колебания синусоидальной формы. Выполнение условий баланса амплитуд и фаз на одной (генерируемой) частоте достигается применением час-точно-избирательных элементов в схеме усилителя, но чаще в цепи обратной связи.

Положительная обратная связь в генераторах бывает внешней и внутренней. Внешняя создается с помощью частотно-зависимых цепей, а внутренняя возникает при работе некоторых электронных приборов в определенных режимах. Для создания генераторов синусоидальных колебаний применяется, как правило, внешняя обратная связь, позволяющая получать более высокую, чем внутренняя, стабильность частоты.

Амплитуду стационарных (незатухающих) колебаний генератора можно найти графически с помощью колебательной характеристики и линии обратной связи. Колебательная характеристика - это зависимость амплитуды основной (первой) Гармоники выходного тока усилителя hi от амплитуды напряже.- йия Ubx поступающего на вход усилителя из цепи обратной связи. Колебательная характеристика нелинейна, так как ее вид определяется параметрами нелинейного элемента - усилителя.