Wi=Li{t{)l2=Lllj2, (113

где i{ti) -ток контура в момент t\, соответствующий его максимальному значению.

Следовательно, равенство (11.2) с учетом выражений (11.1) и (11.3) можно записать так:

После момента времени t\ энергия магнитного поля снова переходит в энергию электрического поля и ток катущки убывает.

ЭДС самоиндукции направлена теперь таким образом, что препятствует убыванию тока. Конденсатор С заряжается. Напряжение на его обкладках возрастает, но имеет полярность, противоположную первоначальной.

В момент времени ti вся энергия магнитного поля снова переходит в энергию электрического поля. НапряЛ'еиие на конденсаторе достигает максимального значения Е, а ток в контуре прекращается.

В течение времени ti - /3 конденсатор разряжается и напряжение на нем падает. Ток в контуре возрастает, но в направлении, противоположном первоначальному. С момента времени ti процесс колебаний повторяется и носит гармонический характер. Так как потерь энергии в идеальном контуре не происходит, то возникшие в нем свободные гармонические колебания являются незатухающими.

Частоту свободных колебаний в контуре /о можно определить из следующих соображений.

При свободных колебаниях к элементам контура (катушка индуктивности и конденсатор) приложено одно и то же напряжение u=Ul = Uc и через них протекает один и тот же переменный ток

Следовательно, емкостное Jc= c/ic== l/(woC) и индуктивное XL=uJiL=(i)oL сопротивления элементов контура на частоте fa также должны быть равны между собой, т. е.

А'=с или со/==г1/(шоС), (11.5)

где шо=2л/о - круговая частота свободных колебаний. Из этого равенства получим

coo=l ZC (11.6)

/o=l/(2n/ZC). (11-7)

Время О - ti, за которое протекает один цикл колебаний напряжения и тока в контуре, т. е. период свободных колебаний, является величиной, обратной частоте:

T,=iiu.; (11-8)

или

отсюда с учетом выражения (11.7) будем иметь

7-о-2я/1С. (11.9)

Реактивное сопротивление элементов контура на частоте /о называют характеристическим или волновым сопротивлением контура р. Учитывая выражение (11.6), получим

p = cooL = l>oC)=/Z/C. (11.10)

Теперь предположим, что свободные колебания за счет энергии, запасенной первоначально в конденсаторе, происходят в реальном контуре, т. е. активное сопротивление контура г не равно нулю.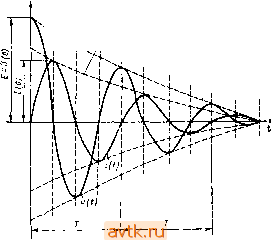

Рис. 11,3

В этом случае за счет потерь энергии на активном сопротивлении амплитуда напряжения и тока в контуре уменьшается по экспоненциальному закону, определяемому выражениями (рис. 11.3)

() = ;/(0)е- ; (11.11)

/(/) = /(0)е- , (11.12)

где f/(0)=£, /(0) - максимальные значения напряжения и тока в начале колебаний; U{t), I{t)-амплитуды напряжения и тока в произвольный момент времени; б - коэффициент затухания Колебаний, который можно определить из формулы

b = rl{2L). (11.13)

Затухание колебаний оценивают также с помощью логарифмического декремента затухания О', равного натуральному логариф-

му отношения амплитуд напряжения (тока), разделенных во вре-мени на период То, т. е.

> = 1п-

U{t)

:1П

U(0) е^С+о^

= ЬТо.

(11.14)

Подставляя в формулу (11.14) выражения для б и Го из (11.9) и (11.12) и учитывая (11.10), получим

8 = яг> C/L=nr/p = nd.

(11.15)

Чем меньше отношение d=r/p, тем медленнее затухают свободные колебания в контуре. Величина, обратная d, называется добротностью контура:

д=1/аГ=р/г=ш г=1/(шоСг). (11.16)

Добротность является важной характеристикой колебательного контура, определяющей его качество. Добротность LC-контуров, применяемых в системах радиосвязи, лежит в пределах 20-300.

Рис. 11.4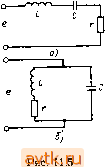

В контурах с очень малой добротностью конденсатор не перезаряжается, и свободные колебания не возникают. Такой процесс, называемый апериодическим, будет происходить, если выполняется неравенство

г>2уТ7С, или г>2р. (11.17)

Учитывая выражение (11.16), из (11.17) найдем добротность контура, при которой возникает апериодический процесс: Q=l/2.

Кривые изменения напряжения и тока в контуре во время апериодического процесса приведены на рис. 11.4.

С физической точки зрения апериодический процесс в контуре означает, что электрическая энергия, накопленная в конденсаторе, за время его разряда полностью переходит в тепловую.

Чтобы получить незатухающие колебания в реальном колебательном контуре, необходимо для восполнения потерь подключить

к контуру источник переменной ЭДС. Колебания в контуре, возникшие под действием подключенного к нему источника переменной ЭДС, называются вынужденными. Если источник ЭДС включают последовательно с катушкой индуктивности и конденсатором, то образованный таким образом контур называют последовательным (рис. 11.5, а).

Контур, в котором источник переменной ЭДС включен параллельно с катушкой и конденсатором, называется параллельным (рис. 11.5, б).

§ 11.2. Вынужденные колебания в последовательном

контуре

Под действием переменной ЭДС e=Esina)t в последовательном контуре протекает переменный ток

i=e/Z, (11.18)

где

Z=r+y(i-c) (И-19)

{Z - полное сопротивление контура); Xl=L, Хс=1/{(иС) - реактивные сопротивления катушки индуктивности и конденсатора. Полное реактивное сопротивление контура

XXi-XcL-l/iioC). (11.20)

Амплитуда тока в контуре определяется выражением

/=£/Z, (11.21)

где

Z=/r2 + [coL-l/(a)C)] (11.22)

- модуль полного сопротивления.

По закону Кирхгофа, напряжение е, приложенное к контуру, складывается из напряжения на конденсаторе с. катушке индуктивности 1 и активном сопротивлении Ur. Амплитуды этих напряжений соответственно равны

UL=fX[ , Uc=IXc, Ur=-Ir. (11.23)

Наглядное представление о характере изменений напряжений и токов в контуре может дать векторная диаграмма (рис. 11.6), Построенная на основании следующих положений. Напряжение на активном сопротивлении совпадает по фазе с током, на конденсаторе оно отстает от тока на 90°, а на индуктивности опережает ток Тоже на 90°. Вектор напряжения Е равен геометрической сумме векторов и и Uc и f/,.

При изменении частоты со источника переменной ЭДС, приложенного к контуру, меняется реактивное сопротивление X контура.

На низких частотах реактивное сопротивление контура имеет емкостный характер, потому что в формуле (11.19) можно пренебречь членом coL, а на высоких частотах - индуктивный, так как в этом случае можно пренебречь членом 1/(иС).

На некоторой частоте ир, называемой резонансной, реактивное сопротивление контура

= copZ.-l/(u)pC) = 0, (11.24)

а полное сопротивление в соответствии с формулой (11.19)

Г . z = r. (11.25)

Рис. и 6 Тогда амплитуда резонансного тока в конту-

ре будет максимальной

/р=£/г. (11.26)

Идеальный последовательный контур (г=0) при резонансе можно считать цепью, замкнутой накоротко.

Из уравнения (11.24) легко найти выражение для резонансной частоты

С0р=1 1С. (11.27)

Сравнивая формулы (11.6) и (11.27), видим, что резонансная частота вынужденных колебаний в последовательном контуре равна частоте собственных колебаний, т. е.

р^шо. (11.28)

Запишем уравнение (11.24) в виде равенства

1/(ШрС) = )р/:. (11.29)

Равенство (11.29) показывает, что при резонансе индуктивное сопротивление последовательного контура по величине равно емкостному.

Умножая левую и правую части равенства на ток /р, получим

/p l/( pC) = W. (11.30)

или, учитывая выражения (11.23), будем иметь

UcU . (11.31)

Таким образом, при резонансе в последовательном контуре амплитуды напряжений на конденсаторе контура Ucp и катушке индуктивности Vlp равны между собой.

Разделив обе части равенства (11.31) на Е, с учетом выраже-й (11.16), (11.23) и (11.26) получим

Ucp/E=и, ,1Е^1, [ 1/( ШрС )] рГ = =pLIr = Q. (И .32)

Выражение (11.32) показывает, что напряжение на катушке индуктивности или конденсаторе последовательного контура при резонансе превышает в Q раз ЭДС источника вынужденных колебаний.

+Асо

Рис. и 7

Рис. 118

Векторная диаграмма напряжений и токов в последовательном контуре при резонансе приведена на рис. 11.7. Векторы напряжений Ucp и Uip равны по величине и противоположны по направлению. Последнее означает, что переменные напряжения ср и Ulp сдвинуты по фазе друг относительно друга на 180°. Вектор напряжения Е совпадает по направлению с вектором тока /р.

Резонансные свойства последовательного контура часто оценивают с помошью коэффициента избирательности по току (Т/= /р, показывающего, во сколько раз уменьшается ток в контуре при отклонении частоты на величину Дсо от резонансного значения сор.

Учитывая выражения (11.21), (11.22) и (11.26), можно запи-

нли, разделив числитель и знаменатель на г, получаем

/1 +{( 1/Г)[1-1/(о>2£С)]}2

(11.33)

(11.34)

Подставляя в формулу (11.34) выражения для Q и Шр из (11.16) и (11.27), находим

или после несложных преобразований

(11.35)

((О-Шр) (ш + (Ор)

При небольших отклонениях частоты а от резонансного значения можно записать

+ >P~2V (11.36)

С учетом принятого допущения выражение (11.35) будет иметь

вид

0,=.-

(11.37)

где Асй= (а - сор) - так называемая расстройка контура.

На основании выражения (11.37) можно построить резонансную кривую контура, характеризующую относительное изменение тока в контуре при его расстройке.

На рис. 11.8 приведено семейство резонансных кривых последовательного контура при различных значениях добротности Q. По этим кривым можно определить полосу пропускания контура 2А(0и, т. е. диапазон частот, в пределах которого ток в контуре превышает значение /р/У^г==:0,707/р. Из рисунка видно, что полоса пропускания расширяется с уменьшением добротности. Действительно, положив в формуле (11.37) ai=l/y2 и выразив 2Аа)=2Аип, получаем

2Aco =a)p/Q. (11.38)

§ 11.3. Вынужденные колебания в параллельном контуре

При подключении переменной ЭДС e=Esm(i)t к колебательному контуру (рис. 11.5, б) в общей цепи схемы будет протекать переменный ток

I=e/Z , (11.39)

где

(П.40)

- эквивалентное сопротивление контура; ii=r + jaL=r + li] -22= 1/(/соС) =-IXc - сопротивления индуктивной и емкостной ветвей контура.

Подставляя выражения для Zi и в (11.40), получаем

у (r+jXOi-jXc-) LiC-JrXc П14П

р области высоких частот обычно выполняется соотношение L/C- р^гХс, поэтому вторым членом числителя в выражении (11.41) можно пренебречь, т. е.

Z,ft=---. - (11.42)

Умножая числитель и знаменатель на г - j{Xl - Хс), выражение (11.42) можно представить следующим образом:

---(11.43)

В соответствии с выражением (11.43) модуль эквивалентного

сопротивления после несложных преобразований определяем по формуле

Za , (11.44)

Амплитуда тока в общей цепи контура

/=£/Z . (11.45)

Амплитуда токов в индуктивной и емкостной ветвях контура

/=£ г2 + 1; (11.46)

1с=Е1Хс. (11.47)

Векторная диаграмма для параллельного контура на частоте, отличной от резонансной, приведена на рис. 11.9, а. На диаграмме вектор тока емкостной ветви /с опережает напряжение источника на 90°, а вектор тока индуктивной ветви II отстает от напряжения источника на угол ф, меньший 90°. Вектор тока в общей цепи контура равен геометрической сумме векторов /с и II.

На резонансной частоте Ир реактивные сопротивления индуктивной и емкостной ветвей контура равны между собой, т. е.

iP=cp или со/=1/(сОрС). (11.48)

Из равенства (11.48) найдем выражение для резонансной частоты вынужденных колебаний в параллельном контуре

cOp=l/-/ZC, (11.49)

Которое совпадает с выражением (11.27) для резонансной частоты в последовательном контуре и выражением (И.б) для частоты Собственных колебаний в контуре.

(11.50)

Как следует из формулы (11.42), при резонансе в параллель-ном контуре эквивалентное сопротивление контура является чисто активным и имеет максимальное значение

Амплитуда тока в общей цепи

/p=£/Z3p=£/(p7r) = £/(Qp) (11.51)

в Q раз меньше, чем амплитуда каждого из токов в индуктивной и емкостной цепях контура:

/ср=Е/Х^=Е1р. (11.53)

Идеальный параллельный контур, где г-О, при резонансе эквивалентен разрыву в цепи. Векторная диаграмма напряжения и токов в параллельном контуре при резонансе приведена на риа 11.9, б. Резонансные свойства параллельного контура имеют различный характер в зависимости от значения внутреннего сопротивления источника сигнала Rr.

При расстройке контура на величину Дш = ш-сор выражение (11.14) для эквивалентного сопротивления контура с учетом допущения (11.36) можно записать следующим образом:

7 - L . (11.54)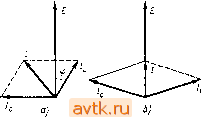

Рис. 11.9

1 +Q2

/ 2Дш \

Если /?г<2эк, то напряжение на контуре остается практически постоянным при всех изменениях частоты, а ток в общей цепи контура обратно пропорционален эквивалентному сопротивлению 2эк В этом случае резонансные свойства контура оценивают с помощью коэффициента избирательности по току

.===l/l+Qf-r. . (11-55)

/р zk У \ < р /

Резонансная кривая, соответствующая формуле (11.55), приведена на рис. 11.10, а.

По резонансной кривой (рис. 11.10, а) определяют полосу пропускания параллельного контура по току 2Дип/, характеризующую

диапазон частот, в пределах которого ток в общей цепи / при расстройке контура превышает ток в общей цепи при резонансе не более чем в У2 раз.

При работе в схемах усилителей и генераторов высокой частоту параллельный колебательный контур подключается обычно к источнику с большим внутренним сопротивлением, т. е. имеем случай /?г>2эк. Тогда напряжение на контуре

и=Е . -(11.56)

изменяется пропорционально напряжение имеет максимальное значение

=EQIR,.

(11.57)

сопротивлению 2эк.

При

резонансе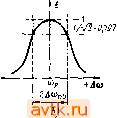

Ток в общей цепи /= = Е1{Яг+1эк) остается практически постоянным при всех изменениях частоты. В этом случае резонансные свойства контура оценивают с помощью коэффициента избирательности по напряжению

Рис. 11.10

Подставляя выражения для 2эк (11.58), получим

(11.50)

(11.58) и (11.54)

в

У 1 + Q2 (2Д(0/и,р)2

(11.59)

На рис. 11.10, б построена резонансная кривая параллельного контура по напряжению, соответствующая выражению (11.59), при г>2эк. По резонансной кривой (рис. 11.10, б) можно определить полосу пропускания контура по напряжению 2A(0nu, определяемую как диапазон частот, в пределах которого напряжение на контуре и превышает значение Ур 2 0,707р.

Положив в формуле (11.59) оу=1/>/и выразив 2А(о = 2Аа)пи, найдем

2Д ) у=Шр/д. (11.60)

Из формулы видно, что полоса пропускания по напряжению Параллельного контура расширяется с уменьшением добротности.

Если /?г соизмеримо с 2эк, то параллельный контур обладает резонансными свойствами по току и напряжению, т. е. ток в общей непч ча резонансной частоте имеет минимальное, а напряжение на Контуре - максимальное значения.